В современной промышленности широкое применение находят композиционные материалы (КМ) и изделия на их основе, так как они обладают значительными преимуществами по сравнению с традиционными металлами и сплавами, обладая уникальными упругими и прочностными свойствами, а также долговечностью работы. Это особенно актуально для авиаконструкций, так как материалы попадают в экстремальные условия работы: повышенные и пониженные температуры, зоны высокой радиации, мощные электромагнитные поля, мощные нагрузки и др. Из композитных материалов производят корпус или детали корпуса, лонжероны лопастей вертолетов и ветроэнов и другие элементы. Применение таких материалов в авиаконструкциях способствует минимизации веса изготавливаемого изделия, повышению удельной прочности, увеличению ресурса и срока службы [1, 2].
Перед авиапредприятиями встают вопросы связанные с обеспечением постоянно возрастающих требований различного рода к материалам авиаконструкций, снижения погрешностей технологий [3]. Для удовлетворения этих требований необходимо использовать качественные исходные материалы, соблюдать технологии их изготовления, создавать современные автоматизированные системы управления. А поэтому необходимо применение математического синтеза на основе глубокого изучения технологических процессов, всесторонняя математическая проработка процесса полимеризации при изготовлении изделий из КМ.
Полный цикл производства КМ включает в себя три этапа: I этап – режим предварительного разогрева; II этап – режим полимеризации; III этап – режим охлаждения. Для исследования технологических процессов необходимы сведения о теплопередаче на всех этапах производства композиционных материалов.
Цель работы – разработать и исследовать математические модели процессов теплопередачи в многослойных цилиндрических изделиях в установках автоматического ведения технологического процесса (АВТП) на всех этапах производства КМ.
Постановка и решение задачи на первом этапе
Первый этап – это режим предварительного разогрева, с которого начинает осуществляться процесс теплопередачи в многослойных цилиндрических изделиях в установках АВТП.
При рассмотрении данного этапа считаем, что между слоями имеет место идеальный тепловой контакт и температура контактирующих поверхностей слоев одинакова. Процесс полимеризации не осуществляется, так как он запускается со второго этапа производства КМ.
Исследуем изделие в форме полого многослойного цилиндра, внутри которого размещается технологический мешок, уложенного в пресс-форму. К пресс-форме подключается электрообогрев. При этом температура может передаваться только в радиальном направлении, так как по длине изделия z и по φ, то есть по цилиндрическим координатам, температура одинакова. Параметр теплопроводности λi 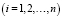 для каждого слоя одинаков, так как слои состоят из одного и того же КМ, но под воздействием температуры могут незначительно изменяться. Величина теплового потока находится в зависимости от глубины проникновения и от начального нагрева.
для каждого слоя одинаков, так как слои состоят из одного и того же КМ, но под воздействием температуры могут незначительно изменяться. Величина теплового потока находится в зависимости от глубины проникновения и от начального нагрева.
Количество имеющихся на сегодняшний день решений таких задач достаточно ограничено. Так, например, при применении преобразований с функцией Грина получены общие результаты, зависящие от граничных условий. Однако с увеличением количества составляющих изделие слоев трудоемкость выполнения необходимых преобразований резко возрастает. Число слоев в рассматриваемых изделиях может доходить до ста.
Исследуемое изделие можно рассматривать как многослойный цилиндр бесконечной длины, так как его длина значительно больше диаметра, то есть 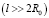 (рис. 1).
(рис. 1).
При сделанных выше предположениях постановку задачи на первом этапе математически можно описать так [4]:
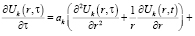
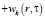 ,
, 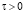 ,
,
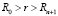 ,
, 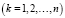 (1)
(1)
начальное условие
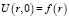 , (2)
, (2)
где Uk – температура в k-ом слое; r – радиус цилиндра; ak – температуропроводность k-ого слоя изделия; wk – функция источников.
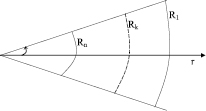
Схема расположения слоев изделия
Запишем в общем виде граничные условия на свободных поверхностях (подбирая соответствующие коэффициенты, можно получить граничные условия I, II или III рода с переменным потенциалом среды и произвольно меняющимся потоком тепла):
при r = R0
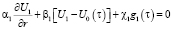 ; (3)
; (3)
при 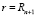
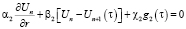 , (4)
, (4)
где U0 и 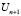 – соответственно температуры на внешней и внутренней поверхности изделия;
– соответственно температуры на внешней и внутренней поверхности изделия;
g1, g2 – потоки тепла с внешней и внутренней поверхностей изделия;
α1, α2, β1, β2, χ1, χ2 – коэффициенты теплообмена между средами.
Кроме того, наложим условия сопряжения между отдельными слоями:
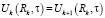 ;
;
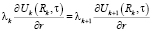 ,
,
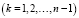 .
.
Методом конечных интегральных преобразований Ханкеля [5] найдем решение исходной задачи для каждого слоя в виде
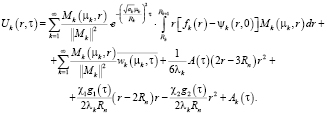 (5)
(5)
Постановка и решение задачи на втором этапе
Процесс полимеризации происходит на втором этапе производства КМ. При этом исследуемое изделие считаем бесконечно полым цилиндром, так как его длина больше диаметра 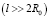 . Цилиндрические координаты φ и z исключаем из рассмотрения, так как изделие находится внутри пресс-формы и тепло распространяется только в радиальном направлении по изотермическим поверхностям, а по длине и по φ теплопередача будет одна и та же.
. Цилиндрические координаты φ и z исключаем из рассмотрения, так как изделие находится внутри пресс-формы и тепло распространяется только в радиальном направлении по изотермическим поверхностям, а по длине и по φ теплопередача будет одна и та же.
Применяя такие предположения, постановка задачи по радиальной схеме в цилиндрической системе координат имеет следующий вид [6]:
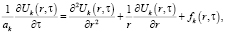
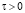 ,
, 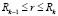 , (6)
, (6)
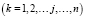 ,
,
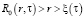 для зоны полимеризации – I,
для зоны полимеризации – I, 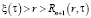 для противоположной зоны – II, при начальных условиях
для противоположной зоны – II, при начальных условиях
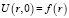 (7)
(7)
и при граничных условиях
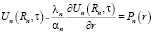 ;
; 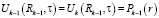 ; (8)
; (8)
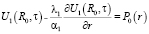 ;
; 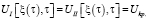 ;
;
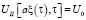 ;
; 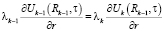 ,
,
при 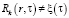 ;
;
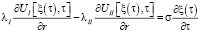 ,
,
где ak, λk, αk – коэффициенты температуропроводности, теплопроводности и теплопередачи; σ – теплота полимеризации; a – безразмерный параметр теплового влияния в k-ом слое; 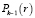 ,
, 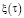 – достаточно гладкие функции своих аргументов, которые подлежат определению через условия (1) и (2);
– достаточно гладкие функции своих аргументов, которые подлежат определению через условия (1) и (2); 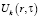 – температура k-го слоя изделия.
– температура k-го слоя изделия.
Используем метод изотермических поверхностей [7] для решения поставленной задачи, при этом заменяем истинное распределение температуры 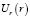 внутри каждой области
внутри каждой области 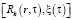 и
и 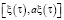 при фиксированных положениях границы
при фиксированных положениях границы 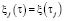 нестационарным распределением температуры
нестационарным распределением температуры 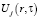 ,
, 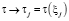 .
.
Итоговое решение задачи имеет вид
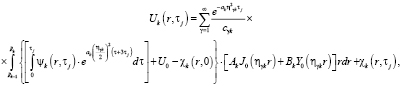 (9)
(9)
где последовательность {τj} определяется рекуррентной формулой
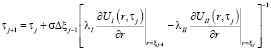 , (10)
, (10)
в которой 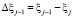 ;
;
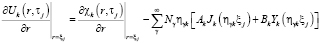 , (11)
, (11)
где
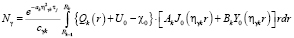 , (12)
, (12)
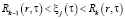 ,
, 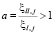 ,
, 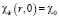 .
.
Постановка и решение задачи на третьем этапе
На третьем этапе производства КМ происходит процесс остывания изделия. Практика показывает, что несоблюдение температурного режима остывания приводит к остаточным термонапряжениям, которые обнаруживаются только в процессе эксплуатации изделий.
Исследованиями установлено, что в производстве лонжеронов лопастей вертолетов в установках АВТП, скорость остывания готового изделия не должна превышать 2–3 градуса в минуту [8]. Нарушение данного процесса остывания приводит к опасным остаточным термонапряжениям. Поэтому необходимо составить математическую модель естественного остывания изделия в установках АВТП в зависимости от температуры окружающей среды, так как АВТП просто отключается от сети после завершения второго этапа производства КМ. Далее изделие охлаждается от температуры полимеризации (160–165 °С) до температуры окружающей среды (цеха).
Лонжероны лопастей вертолетов имеют форму полого цилиндра. Длина изделия значительно длиннее диаметра 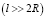 , поэтому изделие можно рассматривать как полый бесконечный цилиндр с внутренним радиусом R0 и с внешним радиусом R.
, поэтому изделие можно рассматривать как полый бесконечный цилиндр с внутренним радиусом R0 и с внешним радиусом R.
Остывание начинается с внешней поверхности изделия, торцы заглушены. В начальный момент времени внешняя поверхность имеет постоянную температуру (температуру цеха, где изготавливается изделие), а изделие имеет температуру полимеризации. Для определения распределения температуры в изделиях в любой момент времени на любой глубине сделаем следующую постановку задачи
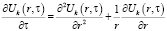 ,
,
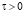 ,
, 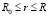 , (13)
, (13)
с начальным условием
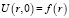 , (14)
, (14)
и граничными условиями
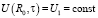 , (15)
, (15)
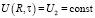 ,
,
где R – радиус внешней поверхности; R0 – радиус внутренней поверхности изделия; 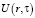 – температура изделия; a – температуропроводность материала; r – переменная в радиальном направлении; τ – время.
– температура изделия; a – температуропроводность материала; r – переменная в радиальном направлении; τ – время.
Так как 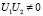 и
и 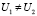 , то ищем решение задачи в виде
, то ищем решение задачи в виде
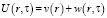 . (16)
. (16)
При этом функция v(r) должна удовлетворять дифференциальному уравнению
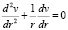 (17)
(17)
и граничным условиям
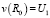 ,
, 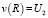 .
.
Функция 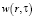 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению
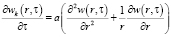 ,
,
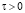 ,
, 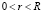 (18)
(18)
при начальном условии
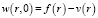
и граничных условиях
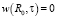 ,
, 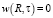 .
.
Применим классический метод Фурье и окончательно получим распределение температуры в изделии в зависимости от r и τ в виде
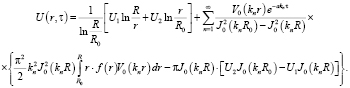 (19)
(19)
Собственные числа kn определяются из уравнения
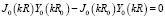 .
.
Заключение
В ходе проведенного исследования разработаны математические модели температурного процесса разогрева, полимеризации и остывания изделия в многослойных цилиндрических конструкциях при производстве КМ в установках АВТП. Полученные аналитические решения позволяют оценить распределение температуры в зависимости от времени в каждом слое изделия на этапах его предварительного разогрева, полимеризации и остывания. Адекватность полученных математических моделей и физических процессов подтверждается реальными экспериментальными исследованиями и тремя актами внедрения на ОАО «Кумертауское авиационное производственное предприятие». Результаты исследования используются для разработки системы управления производством КМ.



