Конструкция спирально-винтового устройства (СВУ) исключительно проста. Стальной спиральный винт, помещенный в рукав, кожух или желоб, приводится во вращение электромотором, который стандартно располагается около выгрузного окна. При этом исходя из наблюдательных данных, радиальный зазор между спиралью и кожухом должен быть достаточно велик для увеличения эффективности транспортировки СВУ. Описанное конструкционное исполнение СВУ имеет ряд неоспоримых эксплуатационных достоинств:
наличие всего одной движущейся части – спирального винта при отсутствии передаточных механизмов от двигателя к рабочему органу;
возможность осуществления перемещения материала по сложным пространственным трассам;
возможность уменьшения диаметра рукава кожуха, что делает его более компактным при сохранении производительности
При этом воздействие самоцентрирующегося гибкого спирального винта при высоком уровне заполнения материалом кожуха обеспечивает бережное транспортирование сыпучей массы, не подвергая ее ударным воздействиям. Но, несмотря на кажущуюся элементарность устроения СВУ, вопрос описания перемещения сыпучего материала по кожуху далек от законченного вида. Устраняя этот пробел, мы осуществляем отыскание выражений, описывающих траекторию частицы в СВУ. При вращении спирального винта по часовой стрелке частица движется по спиральной траектории против часовой стрелки и наоборот. Основываясь на динамическом анализе процесса перемещения и принимая в расчет угол между абсолютной скоростью и тангенциальной скоростью спирального винта 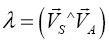 , можно установить требуемые уравнения. При любом радиусе кожуха r абсолютная скорость частиц – VA и каждая частица движется по криволинейной траектории, вообще говоря, совпадающей с хордой эллипса, которая относится к большей полуоси.. Радиус этой кривой имеет вид
, можно установить требуемые уравнения. При любом радиусе кожуха r абсолютная скорость частиц – VA и каждая частица движется по криволинейной траектории, вообще говоря, совпадающей с хордой эллипса, которая относится к большей полуоси.. Радиус этой кривой имеет вид
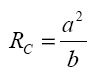 (1)
(1)
где а – большая полуось эллипса, м; b – малая полуось, м. При этом
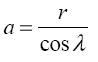 .
.
b=r. Следовательно:
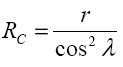 (2)
(2)
Рассмотрим элементарный объем сыпучего материала с весом ΔW. Нормальная сила, действующая на кожух СВТ, обусловлена нормальным давлением Pn и имеет вид
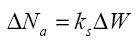 (3)
(3)
где kS – некоторый коэффициент. При этом выражение для центробежной силы имеет вид
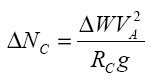 (4)
(4)
Вращательная компонента скорости части выражается через абсолютную
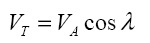 (6)
(6)
Таким образом,
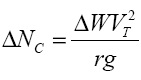 (7)
(7)
Угол подъема винтовой линии α, исходя из простейших геометрических соображений выражается как
 (8)
(8)
Замечая, что
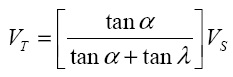 (9)
(9)
и 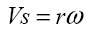 (7) можно переписать в другом виде
(7) можно переписать в другом виде
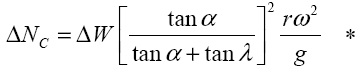
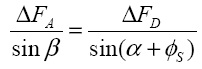 (10)
(10)
где 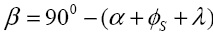 ,
, 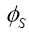 – угол обрушения сыпучего материала со спирального винта. Осевая компонента задается формулой
– угол обрушения сыпучего материала со спирального винта. Осевая компонента задается формулой
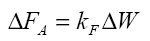 (11)
(11)
коэффициент kF выражается как
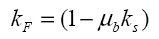 (12)
(12)
где µb – граничный коэффициент трения, который может совпадать с коэффициентом трения между слоями материала или с коэффициентом трения между перемещаемым материалом и материалом кожуха.
Учитывая, что 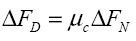 ,
, 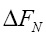 где задается общим уравнением
где задается общим уравнением
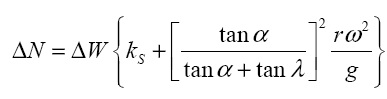 (13)
(13)
Откуда имеем
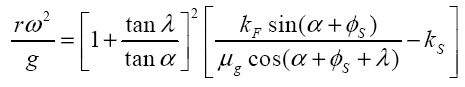 14)
14)
следует заметить, что µg – кинетический коэффициент трения, т.е. соответствует трению между частицами перемещаемого материала и существовании относительного движения между частица
ми. Таким образом, для любых r,ω траектория для частиц может быть установлена.
На периферии СВТ, где частицы соприкасаются с кожухом λ = λ0 и индекс «0» указывает на движении частицы в соприкосновении с кожухом
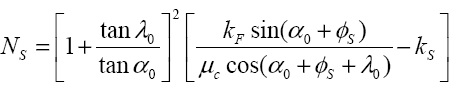 (15)
(15)
Где µc – коэффициент трения между перемещаемым материалом и кожухом СВТ.
В пределе
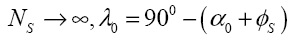 ,
,
т.е. λ0 стремится к некоторому постоянному значению. Таким образом, в данной работе впервые продемонстрирован аналитико-геометрический подход к установлению траектории частицы сыпучего материала в СВТ. Показано, что параметры пространственной кривой жестко связаны с величиной угла 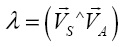 . Исходя из динамического и кинематического анализа, можно прийти к выражению (14) для любого r,ω и (15) на периферии СВТ для определения значения данного угла. Его решение не составляет труда, т.к. представляет собой стандартное тригонометрическое уравнения, в явном виде величина угла может быть получена тривиальной заменой переменных. Но представление решения в явном виде имеет несколько недостатков: исчезновение ясного физико-геометрического смысла уравнения и громоздкость полученного результата. Проведенное исследование подтверждает экспериментальный факт того, что тангенциальное движение частицы противоположно вращению спирального винта, причем результирующая траектория представляет собой кривую, соответствующую хорде некоторого эллипса, меньшая и малая полуоси которогосвязаны с геометрией СВУ.
. Исходя из динамического и кинематического анализа, можно прийти к выражению (14) для любого r,ω и (15) на периферии СВТ для определения значения данного угла. Его решение не составляет труда, т.к. представляет собой стандартное тригонометрическое уравнения, в явном виде величина угла может быть получена тривиальной заменой переменных. Но представление решения в явном виде имеет несколько недостатков: исчезновение ясного физико-геометрического смысла уравнения и громоздкость полученного результата. Проведенное исследование подтверждает экспериментальный факт того, что тангенциальное движение частицы противоположно вращению спирального винта, причем результирующая траектория представляет собой кривую, соответствующую хорде некоторого эллипса, меньшая и малая полуоси которогосвязаны с геометрией СВУ.
Знание особенности траектории частицы в СВУ играет важную роль в анализе перемещения сыпучего материал по кожуху. Кроме того, что вид траектории может указать на присутствие вредоносного для производительности СВУ вращения материала, он указывает на величину собственно перемещения материала. Владея установленными аналитическими выражениями можно определять коэффициент вращательного движения, входящий в выражение для производительности данного устройства. Помимо этого не маловажного факта учет полученных выражений может облегчить расчет конструкционного исполнения СВУ, позволяя инженерам, конструкторам вместо использования эмпирических рекомендаций, руководствоваться представленной методологией. Она обеспечивает более общее основание для конструкционного исполнения СВУ.
Библиографическая ссылка
Исаев Ю.М., Золотарев П.С. ДВИЖЕНИЕ СЫПУЧЕГО МАТЕРИАЛА В СПИРАЛЬНО-ВИНТОВЫХ УСТРОЙСТВАХ // Фундаментальные исследования. – 2009. – № 5. – С. 50-52;URL: https://fundamental-research.ru/ru/article/view?id=1750 (дата обращения: 26.04.2024).



