Метод изоварных характеристик [4] позволяет успешно решать задачи диагностирования при условии успешного выделения чувствительных к ожидаемым дефектам четырехполюсных каналов, для диагностирования объектов различной природы часто используется теория четырехполюсника[3], однако, процедуры выделения четырехполюсной модели из многополюсной разработаны недостаточно полно. Нами предлагается построение этой процедуры на основе формального алгоритма исключения внешнего полюса исходного многополюсника. Предлагаемый метод благодаря своей общности позволяет осуществить переход к любой из шести форм (A, B, Z, Y, G, H) описания четырехполюсника.
Модель регулирования многомерной системы может быть построена на основе использования массива регулировочных признаков, предварительно полученных при анализе системы регулирования, представленной в виде многополюсной системы. Учитывая особенности объекта регулирования (ОР), его топологию и спецификацию, а также характер решаемых задач, можно выделить совокупность величин регулирования, функционально связанных с топологическими характеристиками объекта изучения: такими, как параметры составляющих компонент, топология объекта регулирования, характер связей между компонентами. Назовем эти величины регулирования регулировочными признаками (РП) объекта регулирования.
Для формирования массива регулировочных признаков используем многополюсное представление многомерной системы (рис. 1), которое всегда можно выполнить, если дана структура изучаемой системы и построен топологический граф, имеющий n - вершин и k дуг.
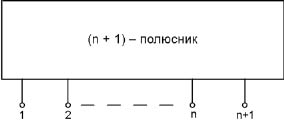
Рис. 1. Многополюсное представление системы
Внутренняя топология объекта регулирования будет представлена совокупностью структурных компонент (СК), характер и размер которых определяется глубиной регулирования и спецификой решаемой задачи. При таком делении ОР, регулирование ведется с глубиной до СК, а весь ОР представляется в виде многополюсной системы. При этом все вершины графа будут представлены полюсами многополюсной системы.
Выбирается функция цели, экстремум которой необходимо добиться при решении задачи регулирования [1] (например, величины запаса работоспособности системы и др.). Формализация поставленной задачи достигается посредством использования аппарата матричных преобразований. Формирование массива регулировочных признаков выполняется на основе использования полной матрицы узловых параметров, построенной на основе топологического графа исследуемой системы. Будем рассматривать только линейные системы. Исследуемая система будет считаться линейной, если полюсные функции внешнего воздействия fs, полюсные функции реакции системы hs и внутренние параметры составляющих компонент системы yij связаны системой линейных урав-
нений.
f1 = y11h1 + y12h2 + ...+ y1(n+1) hn+1
f2 = y21h1 + y22 h2 + ...+ y2(n+1) hn+1 (1)
.......................................
fn = y(n+1)1 h1 + y(n+1)2 h2 + ...+ y(n+1)(n+1) hn+1
Запишем полную матрицу узловых параметров системы:
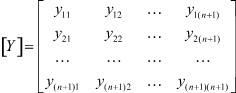
Для вычисления каждого регулировочного признака из всей возможной совокупности регулировочных признаков в топологическом графе необходимо выделить информационный канал, имеющий два полюса на входе (входные полюсы поступления информации) и два полюса на выходе (выходные полюсы съема информации). Соответственно над матрицей [Y] необходимо совершить эквивалентные преобразования, приводящие к понижению ее порядка.
После выполнения таких преобразований многополюсник с любым количеством полюсов преобразуется в четырехполюсник. Эту процедуру назовем процедурой «поглощения» полюсов многополюсной системы. Над матрицей [Y] произведем преобразования, приводящие к получению конечной матрицы четырехполюсной системы.
Для перехода от (n + 1) - полюсной системы к четырехполюснику используем наличие в (n + 1) - полюсной системе полюсов, свободных от поступления и снятия информации.
Предположим сначала, что какой-то k-й полюс имеет полюсную функцию fk, равную нулю, и превращается во внутренний узел (внутреннюю вершину графа).
Тогда из k-го уравнения системы можно выразить полюсную функцию hk через полюсные функции остальных полюсов, при условии fk = 0.
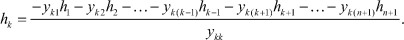
Деля почленно последнее соотношение на ykk и подставляя в исходную систему, получим:
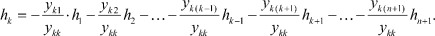
При подстановке в первое уравнение системы (1) получим:
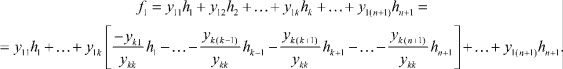
Раскрываем скобки и группируем члены при одинаковых полюсных параметрах h:
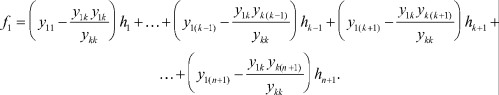
Получили первое уравнение новой системы. Проделав те же преобразования со всеми остальными уравнениями системы (1), получим:

.....................................
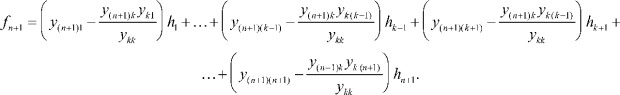
Получили новую систему, в которой будут отсутствовать k-е уравнение и k-й столбец, а коэффициенты при полюсных функциях h будут пересчитаны по формулам, стоящим в скобках перед ними. Соответственно в матрице узловых параметров необходимо вычеркнуть k-ю строку и k-й столбец, что будет соответствовать превращению k-го полюса во внутренний узел (операция поглощения полюса).
Выражения для пересчета коэффициентов в новой системе имеют общий вид:
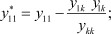
..............................
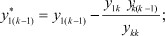
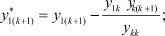
..............................
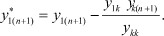
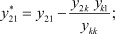
..............................
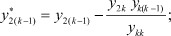
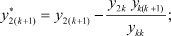
..............................
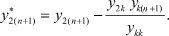
.................................................................
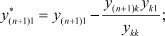
..............................
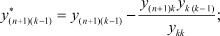
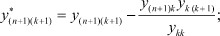
..............................
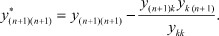
Процедура приведения (n + 1) - полюсника к четырехполюснику предполагает последовательное исключение всех полюсов кроме полюсов выделенного канала передачи информации. Выполнение этой процедуры позволяет найти первый регулировочный признак на основе получения первой конечной матрицы первого четырехполюсника (рис. 2).
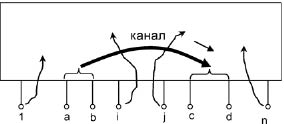
Рис. 2. Выделение каналов передачи информации многополюсника:
ab - вход канала; cd - выход канала
Алгоритм пересчета коэффициентов первой матрицы первого четырехполюсника включает выделение первого информационного канала с полюсами «а», «b» на входе и полюсами «с», «d» на выходе, соответствующим полюсным функциям ia, ib, ic, id в системе (1). Эти полюсы оставляют внешними. Все остальные полюсы преобразуют во внутренние узлы (их полюсные функции считаются равными нулю).
Если обозначить через «k» - количество полюсов, преобразуемых во внутренние узлы, а через «S» - количество полюсов, оставляемых внешними, то k = n + 1 - S, где n + 1 - размер матрицы системы (1).
Выражения для пересчета коэффициентов промежуточных матриц (2) при «поглощении» очередного внешнего полюса получаются при приравнивании коэффициентов при одинаковых полюсных функциях hk:
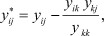 (2)
(2)
где i, j - текущие индексы; k - номер полюса, преобразуемого во внутренний.
После преобразования всех «k» полюсов во внутренние переходим от матрицы (n + 1)-го порядка к матрице S-го порядка (т.е. четвертого).
Аналогичные преобразования необходимо выполнить после выделения в многополюсной системе второго и последующих каналов передачи информации. Общее количество каналов передачи информации определяется комбинаторно и составляет величину M:
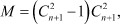
где n + 1 - порядок матрицы [Y];  - количество сочетаний из n + 1 элементов по два.
- количество сочетаний из n + 1 элементов по два.
Полученные в результате приведенных преобразований матрицы четвертого порядка в количестве М служат исходными данными для формирования массива регулировочных признаков системы.
Если задан исходный топологический граф системы, включающий параметры СК (рис. 3), то полная матрица узловых параметров системы будет иметь вид:

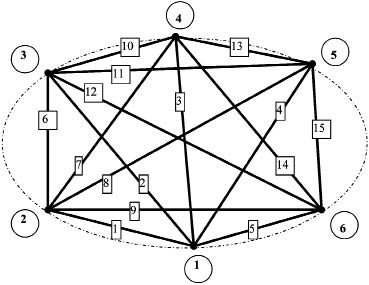
Рис. 3. Топологический граф системы
Приступая к процедуре исключения полюсов, оставляем внешними полюсы 1, 2, 5, 6. Полюсы 3,4 преобразуем во внутренние узлы, используя формулу для пересчета коэффициентов системы (2). Процедура выполняется последовательно с каждым полюсом.
В качестве языка для написания программ используем язык программирования системы MathCad 13.
1. Сначала преобразуем третий полюс.
Получим новую матрицу пятого порядка:

2. Полученную после исключения третьего полюса матрицу считаем исходной. Далее преобразуем четвертый полюс во внутренний. Получим новую матрицу четвертого порядка:
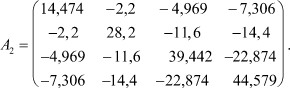
Матрица A2 является матрицей четырехполюсника.
Если превращать во внутренние узлы сразу «k» полюсов, то оставшиеся элементы новой матрицы S-го порядка, полученной вычеркиванием строк и столбцов, отвечающих всем полюсам, превращаемым во внутренние, находятся по формуле:
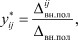 (3)
(3)
где Δвн.пол - определитель, получаемый из определителя матрицы параметров (n + 1)-порядка путем вычеркивания строк и столбцов, соответствующих всем оставшимся внешним полюсам.
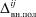 - определитель, получаемый из определителя Δвн.пол путем восстановления строки i и столбца j .
- определитель, получаемый из определителя Δвн.пол путем восстановления строки i и столбца j .
Действительно, если, например один k-й полюс превратить во внутренний, то определитель Δвн.пол = ykk и получается путем вычеркивания строк и столбцов, соответствующих всем оставшимся внешним полюсам.
Определитель 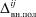 в этом случае получается из определителя Δвн.пол путем восстановления строки i и столбца j.
в этом случае получается из определителя Δвн.пол путем восстановления строки i и столбца j.
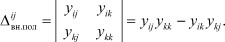
Подставив в соотношение (3), получим:
yij* = (yijykk - yikykj)/ykk = yij - yikykj / ykk,
что соответствует выражению (2).
Таким образом, понижение порядка исходной матрицы узловых параметров исследуемой системы упрощает процедуру нахождения определителя матрицы: количество операций и необходимый объем зарезервированной памяти ЭВМ при вычислении миноров и алгебраических дополнений сокращается.
Полученная в результате эквивалентных преобразований конечная матрица А2 приводит к эквивалентному четырехполюснику и преобразованному конечному графу
(рис. 4, 5).
Рис. 4. Эквивалентный четырехполюсник:
полюсы 1-2 соответствуют а - b;
полюсы 5-6 соответствуют с - d
Структурные компоненты конечного графа имеют соответствующие значения y12* = 2,2; y13* = 4,969; y14* = 7,306; y23* = 1,6; y24* = 14,4; y34* = 22,874.
Если рассматривается (n + 1) - полюсная система, описываемая полной матрицей (n + 1)-го порядка, то такая система является линейно зависимой и любое уравнение системы (1) является линейной комбинацией остальных уравнений системы. В этом случае для получения линейно независимой системы необходимо один из полюсов (например (n + 1)-й ) принять за опорный, а в матрице (n + 1)-го порядка вычеркнуть (n + 1)-й столбец и (n + 1)-ю строку.
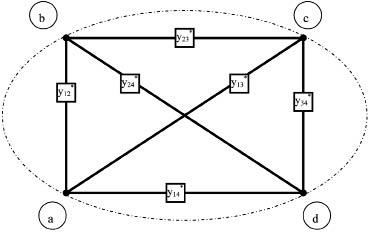
Рис. 5. Конечный граф
Полученная матрица называется укороченной, а соответствующая ей система линейных уравнений - линейно независимой. Именно такая система используется для решения задачи анализа, т.е. для нахождения полюсных функций реакции hk. При решении задачи регулирования для формирования массива регулировочных признаков можно использовать как полную (n + 1)-го порядка матрицу узловых параметров, так и укороченную матрицу n-го порядка.
При использовании укороченной матрицы узловых параметров для определения регулировочных признаков необходимо аналитически связать полюсные функции внешнего воздействия fs и полюсные функции реакции системы hs. В соответствии с преобразованной матрицей системы А2 и согласно теореме Крамера, любая полюсная функция реакции hk равна:
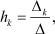 (4)
(4)
где Δ - определитель укороченной матрицы узловых параметров, полученной из полной матрицы А2 вычеркиванием четвертой строки и четвертого столбца при принятии полюса d = 4 за опорный полюс; Δk - определитель, полученный из определителя Δ после замены k-го столбца столбцом полюсных функций воздействия f1, f2, f3. После разложения определителя Δk по элементам k-го столбца, получим следующее соотношение:
Δk = f1Δ1k + f2Δ2k + f3Δ3k, (5)
где Δ1k - алгебраическое дополнение, полученное из определителя Δk после вычеркивания первой строки и k-го столбца; Δ2k - алгебраическое дополнение, полученное из определителя Δk после вычеркивания второй строки и k-го столбца; Δ3k - алгебраическое дополнение, полученное из определителя Δk после вычеркивания третьей строки и k-го столбца.
В силу того, что входные полюсы канала прохождения информации (а = 1 и b = 2) уже зафиксированы изначально, то в выражении (5) необходимо сначала положить f2 = 0 и f3 = 0 и получить соответственно: Δk = f1Δ1k , а затем в том же выражении положить f1 = 0 и f3 = 0 и получить соответственно: Δk = f2Δ2k.
Подставив полученные выражения в соотношение (4), получим выражения для k-й функции реакции системы при подключении воздействия f1 к полюсам а - d (а = 1; d = 4):
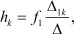
и выражение для k-й функции реакции системы при подключении воздействия f2 к полюсам b - d (b = 2; d = 4, где d - полюс, принятый за опорный).
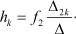
В соответствии с представлением конечного графа (рис. 5), выбранного канала прохождения информации и опорного полюса, можно записать все выражения для функций реакции системы при различных подключениях воздействия.
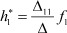 - функция реакции первого полюса при воздействии f1 на первый полюс;
- функция реакции первого полюса при воздействии f1 на первый полюс;
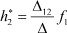 - функция реакции второго полюса при воздействии f1 на первый полюс;
- функция реакции второго полюса при воздействии f1 на первый полюс;
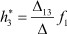 - функция реакции третьего полюса при воздействии f1 на первый полюс;
- функция реакции третьего полюса при воздействии f1 на первый полюс;
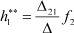 - функция реакции первого полюса при воздействии f2 на второй полюс;
- функция реакции первого полюса при воздействии f2 на второй полюс;
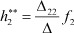 - функция реакции второго полюса при воздействии f2 на второй полюс;
- функция реакции второго полюса при воздействии f2 на второй полюс;
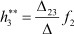 - функция реакции третьего полюса при воздействии f2 на второй полюс;
- функция реакции третьего полюса при воздействии f2 на второй полюс;
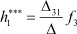 - функция реакции первого полюса при воздействии f3 на третий полюс;
- функция реакции первого полюса при воздействии f3 на третий полюс;
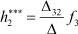 - функция реакции второго полюса при воздействии f3 на третий полюс;
- функция реакции второго полюса при воздействии f3 на третий полюс;
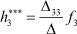 - функция реакции третьего полюса при воздействии f3 на третий полюс.
- функция реакции третьего полюса при воздействии f3 на третий полюс.
Полученные выражения необходимы для дальнейшего формирования массива регулировочных признаков, используемых для построения модели параметрического регулирования систем. В качестве регулировочных признаков выберем коэффициенты передачи [2], так как эти параметры характеризуют систему и зависят только от ее внутренней организации, топологии и спецификации ее СК и не зависят от внешних полюсных функций.
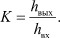 (6)
(6)
Для выбранного канала передачи информации (a-b - вход; c-d - выход, инцидентный опорному полюсу) и опорного полюса d выражение для 3-й узловой функции реакции системы h3* при подключении воздействия f1 к полюсу а (а = 1) получим для функции реакции третьего полюса: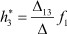 - функция реакции третьего полюса при воздействии f1 на первый полюс.
- функция реакции третьего полюса при воздействии f1 на первый полюс.
Соответственно выражение для 3-й узловой функции реакции системы 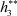 при подключении воздействия f2 к полюсу b (b = 2) получим для функции реакции третьего полюса:
при подключении воздействия f2 к полюсу b (b = 2) получим для функции реакции третьего полюса: 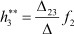 - функция реакции третьего полюса при воздействии f2 на второй полюс.
- функция реакции третьего полюса при воздействии f2 на второй полюс.
В соответствии с принципом суперпозиции для линейных систем можно записать функцию реакции третьего полюса от суммарного воздействия:
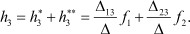
В силу того, что функции воздействия на входе, не инцидентном опорному полюсу, связаны соотношением f2 - f1 = 0, получим:
f2 = f1.
Подставляя это условие в последнее равенство, получим следующее соотношение для h3:
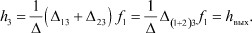
Покажем справедливость последнего соотношения в общем в виде: пусть дан определитель матрицы А2 четвертого порядка:
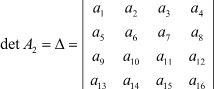

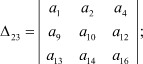
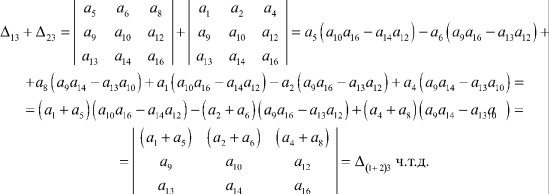
Таким образом, при сложении миноров Δ13 и Δ23 определителя Δ необходимо вычеркнуть третий столбец, а первую строку сложить со второй.
Полученная реакция третьего полюса h3 является выходным параметром системы.
Для определения входного параметра системы рассмотрим функцию реакции первого полюса при воздействии f1 на первый полюс а (а = 1):
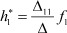 - функция реакции первого полюса при воздействии f1 на первый полюс.
- функция реакции первого полюса при воздействии f1 на первый полюс.
Соответственно реакцию первого полюса h1** при подключении воздействия f2 к полюсу b (b = 2) получим для функции реакции первого полюса:
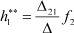 - функция реакции первого полюса при воздействии f2 на второй полюс.
- функция реакции первого полюса при воздействии f2 на второй полюс.
В соответствии с принципом суперпозиции для линейных систем можно записать функцию реакции первого полюса от суммарного воздействия:
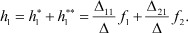
В силу того, что функции воздействия на входе, не инцидентном опорному полюсу, связаны соотношением f2 - f1 = 0, получим:
f2 = f1.
Подставляя это условие в последнее равенство, получим следующее соотношение для h1:
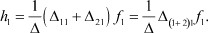
Далее рассмотрим функцию реакции второго полюса при воздействии f1 на первый полюс;
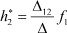 - функция реакции второго полюса при воздействии f1 на первый полюс;
- функция реакции второго полюса при воздействии f1 на первый полюс;
Соответственно реакцию второго полюса при воздействии f2 на второй полюс b (b = 2):
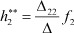 - функция реакции второго полюса при воздействии f2 на второй полюс;
- функция реакции второго полюса при воздействии f2 на второй полюс;
В соответствии с принципом суперпозиции для линейных систем можно записать функцию реакции второго полюса от суммарного воздействия:
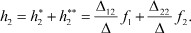
В силу того, что функции воздействия на входе, не инцидентном опорному полюсу, связаны соотношением f2 - f1 = 0, получим:
f2 = f1.
Подставляя это условие в последнее равенство, получим следующее соотношение для h2:
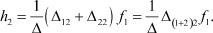
Полученная реакция входного полюса h2 является одним из входных параметров системы.
Для получения входного параметра hвх находим разность h1 - h2:
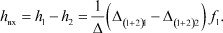
Далее находим один из M (M=(C2n+1 - 1) C2n+1) регулировочных признаков, равный коэффициенту передачи от входа канала передачи информации, не инцидентного опорному полюсу, к выходу канала, инцидентному опорному полюсу.
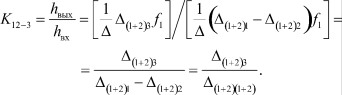
Справедливость последнего соотношения в общем в виде выполним на примере определителя матрицы третьего порядка: (Δ(1+2) 1 - Δ(1+2) 2) = Δ(1+2) (1+2).
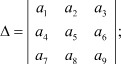
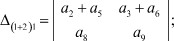
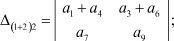
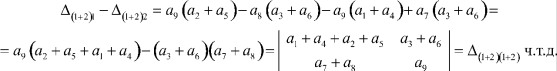
Таким образом разность миноров Δ(1 + 2)1 - Δ(1 + 2)2 определителя Δ эквивалентна минору, получаемому из определителя Δ при сложении первой и второй строки, а также первого и второго столбца.
Возвращаясь к рассмотренному выше примеру матрицы А, выбранному каналу передачи информации и полученной матрицы четырехполюсника А2, вычислим регулировочный признак К12 - 3 , соответствующий выбранному каналу 1-2 - 5-6 исходного графа:
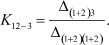
Предварительно находим определитель укороченной матрицы:
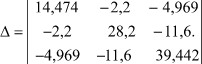
Находим минор Δ(1+2)3:
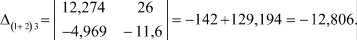
Находим минор Δ(1+2)(1+2):
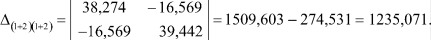
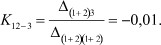
В результате проделанной процедуры получен один из возможных регулировочных признаков К12 - 3, который может быть использован при построении модели регулирования системы. Для нахождения всей совокупности регулировочных признаков необходимо выполнить аналогичную процедуру «поглощения» полюсов и вычисления коэффициента передачи для очередного выбранного информационного канала. В результате формируется массив всех возможных регулировочных признаков, из которого впоследствии выбирается подмножество признаков, используемых для построения модели регулирования.
Таким образом, рассмотренная процедура позволяет понизить порядок исходной матрицы узловых параметров системы и свести матрицу произвольного порядка всегда к матрице четырехполюсника с фиксированными полюсами входа и выхода системы.
Алгоритм разработанной процедуры в виде блок-схемы представлен на рис. 6.
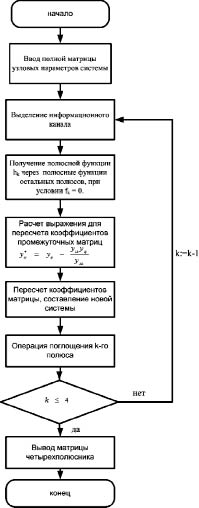
Рис. 6. Блок-схема алгоритма преобразования полной полюсной матрицы многополюсника
к эквивалентной матрице четырехполюсника
Рассмотренная процедура легко формализуема при машинной обработке информации, что расширяет возможности разработчика при решении задач идентификации и параметрического регу-
лирования.
Список литературы
- Блинов Э.К., Розенберг Г.Ш. Техническое обслуживание и ремонт судов по состоянию: Справочник. - СПб.: Судостроение, 1992.
- Выбор информативных параметров при контроле качества изделий информационной техники / Д.В. Гаскаров и др. - Л.: ЛДНТП, 1979.
- Демирчян К.С., Бутырин П.А. Моделирование и машинный расчет электрических цепей. - М.: Высшая школа, 1988.
- Портнягин Н.Н., Пюкке Г.А. Теория, методы и эксперименты решения задач диагностики судовых электрических средств автоматизации: монография - СПб.: Судостроение, 2004 - 157 с.
Рецензенты:
Потапов В.В., д.т.н., профессор кафедры промышленной теплоэнергетики и электроснабжения филиала ДВГТУ в г. Петропавловск-Камчатский;
Шулюпин А.Н., д.т.н., и.о. зам директора НИГТЦ ДВО РАН по научной работе, г. Петропавловск-Камчатский;
Пен Р.З., д.т.н., профессор, профессор кафедры целлюлозно-бумажного производства ГОУ «Сибирский государственный технологический университет», г. Красноярск;
Кирьянов Б.Ф., д.т.н., профессор, профессор кафедры прикладной математики и информатики, Новгородский государственный университет имени Ярослава Мудрого, г. Великий Новгород.
Работа поступила в редакцию 22.10.2010.
Библиографическая ссылка
Портнягин Н.Н., Пюкке Г.А., Горева Т.И., Горева Т.С. ИСПОЛЬЗОВАНИЕ МЕТОДА ИСКЛЮЧЕНИЯ ВНЕШНЕГО ПОЛЮСА МНОГОПОЛЮСНИКА ПРИ ПОСТРОЕНИИ МОДЕЛИ РЕГУЛИРОВАНИЯ МНОГОМЕРНЫХ СИСТЕМ // Фундаментальные исследования. – 2011. – № 8-1. – С. 157-166;URL: https://fundamental-research.ru/ru/article/view?id=26805 (дата обращения: 27.04.2024).



