Высокопористые ячеистые материалы (ВПЯМ) являются перспективным классом материалов и получают в настоящее время свое применение в различных областях промышленности, транспорта в качестве носителей катализаторов, интенсификаторов массо- и теплообмена, газораспределителей, разделителей парогазовых сред, токоприемников для топливных элементов, звукопоглощающих и композиционных материалов. Они имеют высокую пористость (от 78 до 97 %) и проницаемость, развитую регулируемую поверхность, малый объем, прочность при сжатии 0,4–0,8 МПа [1]. Размер ячейки 0,3–4,0 мм. ВПЯМ могут быть изготовлены из металлов (металлические ВПЯМ, открытоячеистые пенометаллы, англ. open-cell metal foam) и их оксидов (керамические ВПЯМ, открытоячеистая пенокерамика, англ. open-cell ceramic foam). Высокопористые ячеистые материалы можно получить различными способами [7]. Наиболее часто их изготавливают пропиткой пенополиуретана исходным шликером с последующим выжиганием полимерной матрицы. Совокупность свойств ВПЯМ позволяет рекомендовать их к использованию в качестве носителей катализаторов в процессах, где необходимо сочетание низких гидравлических потерь и эффективного массообмена газового потока с поверхностью катализатора [8], например, для очистки дымовых газов или проведения быстрых жидкофазных процессов.
Целью данной работы являлось проведение компьютерного моделирования течения смеси отходящих газов через слой высокопористого ячеистого материала с последующим анализом режимов и характеристик течения.
Моделирование газодинамической обстановки в данной работе выполнено в трехмерной постановке из-за сложной структуры потоков внутри слоя ВПЯМ.
Математическая модель
В качестве геометрической модели ячейки высокопористого материала использовалась сферическая модель с двенадцатью отсеченными сферическими сегментами (рис. 1) [5]. Каждая ячейка имеет 12 соседних, образуя вместе с ними ансамбль из 13 элементарных ячеек, соответствующий гранецентрированной кубической упаковке сфер с перекрытиями. Такая структура имеет всего 2 определяющих параметра: диаметр сферы (ячейки) и степень сохранения как отношение расстояния между центрами сфер к диаметру сферы. Степень сохранения однозначно связана [5] с долей свободного объема (пустот) модели, которая, в свою очередь, соответствует макропористости ВПЯМ.
В пакете GAMBIT® была построена многослойная модель из 21 слоя ячеек с неравномерной тетраэдральной конечно-объемной сеткой (1,0 млн конечных объемов), шагом на увеличение от стенки hw = 1,2. Моделирование показало линейное распределение давления по слою вдоль направления потока, поэтому данная модель использовалась в качестве модели участка ВПЯМ, перепад давления P21l на нем рассчитывался по формуле:
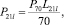 (1)
(1)
где P70– перепад давления на слое (70 мм) ВПЯМ; L21l – длина модели, мм.
Также была построена модель канала блочного сотового материала, сечение канала – квадратное с площадью 1 мм2, длина – L21l (сетка – 197 тыс. конечных объемов, hw = 1,2).
а б
б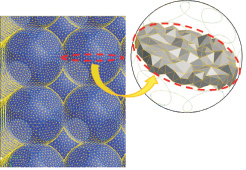
Рис. 1. Геометрическая модель участка ВПЯМ:
а – часть структуры геометрической модели; б – тетраэдральная конечно-объемная сетка
Направление газового потока было выбрано вдоль длинной оси модели. На крайних окнах модели, перпендикулярных потоку, задавались периодические граничные условия.
Для моделирования движения вязкой среды численно решались осредненные по Рейнольдсу трехмерные стационарные уравнения Навье-Стокса (RANS). Между входными и выходными отверстиями в модели задавался перепад давлений, на стенке – граничное условие прилипания потока. Моделирование было выполнено в программном пакете ANSYS® FLUENT®. Для замыкания математической модели использовалась k–ε RNG модель турбулентности со стандартными параметрами, которая обеспечивает достаточную точность при расчете дозвуковых течений [10]. В пристеночной области использовался подход расширенных функций стенки (enhanced wall treatment), безразмерное расстояние до стенки y + во всех опытах не превышало числа 5.
Толщина исследуемого участка – 70 мм. Диаметр ячейки – 2,109 мм (крупноячеистый ВПЯМ, КЯ) и 1,007 мм (мелкоячеистый ВПЯМ, МЯ). Степень сохранения геометрической модели (0,92) соответствовала пористости моделируемого реального образца 90 %.
На вход в модель подавался слабо турбулизованный поток (интенсивность турбулентности – 5 %). В области низких скоростей интенсивность турбулентности быстро затухала по модели, то есть турбулентные структуры были неустойчивы. Это означало ламинарное течение среды, и вместо k–ε-модели далее решалась ламинарная модель.
Исследование перепада давлений на ВПЯМ
Зависимость перепада давлений от скорости газового потока для двух различных ВПЯМ и сотового материала представлена в виде графиков на рис. 2.
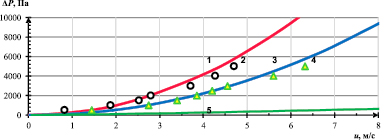
Рис. 2. Зависимость перепада давлений от скорости газового потока. Толщина слоя – 70 мм^
1 – МЯ, модель; 2 – эксперимент dЯ = 1 мм [9]; 3 – КЯ, модель; 4 – эксперимент
dЯ = 2,109 мм [9]; 5 – сотовый материал, модель
Как видно из рис. 2, гидравлическое сопротивление у мелкоячеистых образцов выше, то есть с уменьшением диаметра ячейки гидравлическое сопротивление увеличивается. Результаты согласуются с данными эксперимента [9]. У ВПЯМ гидравлическое сопротивление выше в 10–25 раз, чем у блочного сотового материала.
На рис. 3 показано сравнение расчетных и экспериментальных значений скорости при фиксированных значениях перепада давлений для крупноячеистого (рис. 3а) и мелкоячеистого (рис. 3б) ВПЯМ. Как видно из рис. 3, в диапазоне скоростей более 1,5 м/с относительная ошибка расчета по модели не выходит из 20 %-го коридора. Многослойная модель хорошо согласуется с экспериментальными данными и может быть использована в качестве геометрической модели участка высокопористого ячеистого материала.
а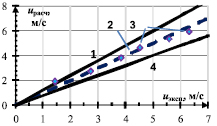 б
б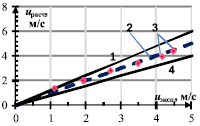
Рис. 3. Сравнение расчетных и экспериментальных значений скорости при фиксированных значениях перепада давлений для КЯ (а) и МЯ (б):
1 – линия относительной ошибки – 20 %; 2 – эксперимент [9]; 3 – многослойная модель;
4 – линия относительной ошибки + 20 %
Полученные зависимости в диапазоне 0–10 м/с с относительной погрешностью менее 10 % ложатся на квадратичные кривые вида
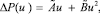 (2)
(2)
где u – скорость газа в потоке;  и
и 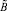 – коэффициенты, найденные с помощью метода наименьших квадратов (МНК):
– коэффициенты, найденные с помощью метода наименьших квадратов (МНК): 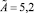 ,
, 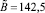 для КЯ,
для КЯ, 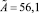 ,
, 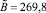 для МЯ.
для МЯ.
Анализ режимов фильтрации газа
Следует заметить, что двучленная запись для фильтрации жидкостей и газов вида (2) применяется для описания зависимости гидравлического сопротивления пористых образцов от скорости потока в турбулентном режиме. В работе [3] было показано, что зависимость ∆P/L = f(u) на образцах ВПЯМ нелинейна (что означает отклонение от линейного ламинарного закона Дарси) при скоростях фильтрации газа больше 0,23 м/с. Таким образом, при указанных скоростях для образцов [3] течение было неламинарно.
При моделировании течения газа в слое ВПЯМ зависимость гидравлического сопротивления от скорости потока была также нелинейна и представляла собой квадратичную зависимость с малым начальным линейным участком.
В статьях [2, 3] на основе экспериментальных данных построены зависимости критического значения числа Рейнольдса от пористости в металлических ВПЯМ. При пористости 90 % это значение составляет ≈ 11. При этом авторы отмечают, что скорость газового потока u для Reкр составляла 0,1 м/с. Похожие данные представлены в статье [6], которые свидетельствуют о том, что в ячеистых высокопористых материалах турбулизация газового потока наблюдается уже при скорости u = 0,05 м/с.
По результатам численного эксперимента была построена зависимость коэффициента сопротивления от числа Рейнольдса в логарифмических координатах (рис. 4).
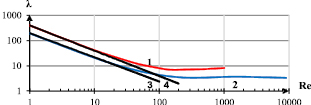
Рис. 4. Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса;
1 – МЯ; 2 – КЯ; dЯ = 2,109 мм; 3, 4 –касательные
Величину Re для ячейки определяли из выражения:
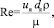 (3)
(3)
где ρ – плотность газовой среды; uя – средняя скорость газа в центральном сечении ячейки; dя – диаметр ячейки; μ – динамическая вязкость газа.
Коэффициент гидравлического сопротивления λ можно вычислить по формуле:
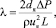 (4)
(4)
где L – длина моделируемого образца ВПЯМ (здесь 70 мм).
Для ВПЯМ значение Reкр, соответствующее началу отклонения зависимости от линейной, приблизительно равно 11, что совпадает с данными [8]. Равенство критического значения числа Рейнольдса является следствием гидродинамического подобия потоков в мелкоячеистых и крупноячеистых моделях ВПЯМ. При этом скорость газа составляла для крупноячеистого ВПЯМ 0,067 м/с, что хорошо согласуется с экспериментальными данными [6], для мелкоячеистого 0,128 м/с.
Об инвариантности λ(Re) (окончание переходного режима течения, развитая турбулентность) можно говорить, начиная с Re > 250. При этом скорость газа в потоке для крупноячеистого ВПЯМ u > 1,79 м/с (u > 2,32 м/с для мелкоячеистого).
Коэффициент гидравлического трения для мелкоячеистого ВПЯМ в среднем в три раза выше, чем для крупноячеистого, в рассматриваемом диапазоне скоростей (0–12 м/с).
Исследование характеристик турбулентности
Использование параметрической модели позволяет в случае турбулентного течения вычислить его осредненные характеристики. В данной работе для определения характера течения вычислены следующие параметры:
– интенсивность турбулентности;
– турбулентная вязкость;
– колмогоровские масштабы, характеризующие самые мелкие турбулентные вихри;
– завихренность, как циркуляция потока через единицу площади.
На рис. 5 показан профиль Z-составляющей вектора завихренности в слое крупноячеистого ВПЯМ (сечение вдоль слоя) при перепаде давлений 4000 Па, поток направлен по оси X. По приведенной картине можно сделать вывод, что наибольшая степень завихренности наблюдается около стенки перед и после прохождения потоком окон.
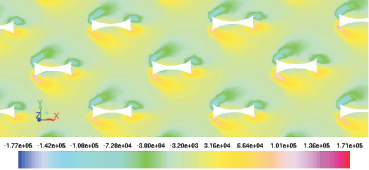
Рис. 5. Профиль Z-составляющей вектора завихренности
в слое КЯ при перепаде давлений 4000 Па
Масштаб турбулентности, указывающий размеры наиболее крупных турбулентных вихрей [4]:
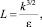 (5)
(5)
где k – кинетическая энергия турбулентности, м2/с2; ε – диссипация кинетической энергии турбулентности, м2/с3.
Как видно из рис. 6а, наибольший размер вихрей наблюдается при скоростях порядка 2 м/с, с дальнейшим ростом скорости его значение начинает уменьшаться. Это обусловлено тем, что крупные вихри (наибольшие, длинноволновые моды частных решений уравнений Навье-Стокса) теряют устойчивость с ростом скорости.
а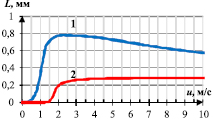 б
б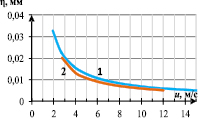
Рис. 6. Зависимость масштаба турбулентности от скорости газового потока:
а – наибольший масштаб турбулентности L;
б – Колмогоровский масштаб длины η; 1 – КЯ; 2 – МЯ
Колмогоровский масштаб длины определяет наименьшие размеры вихрей [4]:
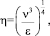 (6)
(6)
где ν – кинематическая вязкость среды, м2/с.
Зависимость Колмогоровского масштаба длины η от скорости движения газового потока представлена на рис. 6б. Колмогоровские масштабы вычисляются для развитого турбулентного течения и при низких скоростях зависимости не строятся.
Заметно, что масштабы мелких вихрей в 60–100 раз меньше масштабов крупных вихрей при развитом турбулентном режиме. С ростом скорости масштабы медленно уменьшаются, стремясь к постоянной величине – минимальному Колмогоровскому размеру вихря, размеры которого менее 0,005 мм.
Колмогоровский временной масштаб, указывающий среднее время жизни вихрей, непосредственно диссипирующих в тепло [4]:
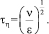 (7)
(7)
Как видно из зависимости временного масштаба мелких вихрей от скорости газа (рис. 7), наибольшее время жизни мелких вихрей соответствует наименьшим скоростям развитого турбулентного потока. С увеличением скорости газа дальнейшее развитие турбулентности происходит в направлении уменьшения времени жизни мелких вихрей, то есть процесс диссипации кинетической энергии в тепловую происходит быстрее.
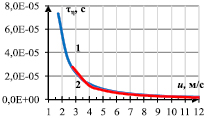
Рис. 7. Зависимость Колмогоровского временного масштаба турбулентности от скорости газового потока:
1 – крупноячеистый ВПЯМ, dЯ = 2,109 мм;
2 – мелкоячеистый ВПЯМ, dЯ = 1,007 мм
Полная (эффективная) вязкость потока складывается из постоянной (динамическая вязкость) и пульсационной составляющих (турбулентная, или вихревая, вязкость). С развитием турбулентного течения турбулентная вязкость начинает доминировать над динамической вязкостью. В ячейке крупноячеистого ВПЯМ это происходит по достижении скоростью потока значения 1,2 м/с. Вычисление аналогичных показателей в окнах между ячейками показало, что в них турбулентная вязкость растет медленнее и начинает доминировать над динамической вязкостью при скорости 2 м/с (рис. 8).
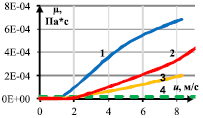
Рис. 8. Зависимость турбулентной вязкости от скорости газа при установившемся течении:
1, 2 – средняя турбулентная вязкость в центральном сечении ячейки, крупно- и мелкоячеистый ВПЯМ, 3 – средняя турбулентная вязкость в выходных окнах ячеек, 4 – динамическая вязкость (постоянная среды)
Формула Колмогоровского масштаба скорости из анализа размерностей [4]:
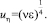 (8)
(8)
Отношение средней скорости пульсационного движения мелких вихрей к средней скорости среды в ячейке есть средняя интенсивность турбулентности мелких вихрей:
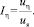 (9)
(9)
На рис. 9 показана зависимость средней интенсивности турбулентности мелких вихрей от скорости газового потока. При турбулентном течении с увеличением скорости интенсивность мелкомасштабных пульсаций уменьшается, так как уменьшается размер мелких вихрей, а следовательно, их энергия, и скорость мелкомасштабных пульсаций начинает расти медленнее средней скорости потока.
Сравнение блочного сотового и ячеистого материала
по интенсивности турбулентности
На рис. 10 приведена зависимость средней интенсивности турбулентности от скорости газового потока. Интенсивность турбулентности вычислялась как отношение среднеквадратичного составляющих 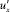 ,
, 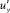 ,
, 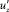 вектора пульсационной скорости к средней скорости движения
вектора пульсационной скорости к средней скорости движения
среды uср [10]:
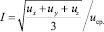 (10)
(10)
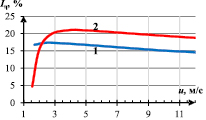
Рис. 9. Зависимость интенсивности турбулентности мелких вихрей от скорости газового потока:
1 – КЯ; 2 – МЯ
За среднюю скорость движения среды принималась средняя скорость движения потока в центральном сечении ячеек.
Согласно рис. 10, данная зависимость в рассматриваемом интервале скоростей является кривой с насыщением, для КЯ при росте скорости течения газа интенсивность турбулентного течения стремится к постоянной величине в 54 %.
Сравнивая данную зависимость с зависимостью на рис. 9, можно отметить, что интенсивность пульсационного движения мелкомасштабных вихревых структур приблизительно в 2–3 раза ниже, чем крупных.
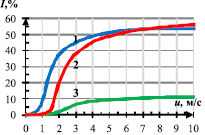
Рис. 10. Зависимость интенсивности турбулентности от скорости
газового потока:
1 – КЯ; 2 – МЯ; 3 – блочный сотовый материал, ширина канала a = 1 мм
Выводы
Построена геометрическая модель, основанная на плотной упаковке сфер с пересечениями в трёхмерном пространстве. Модель состоит из массива ячеек, уложенных в узлы гранецентрированной кубической решетки. Ячейка модели соответствует поре ВПЯМ. С помощью пакета конечного анализа FLUENT произведено численное решение RANS в стационарной постановке, для замыкания системы использована k–ε RNG модель [10].
По результатам численного эксперимента (длина слоя L = 70 мм, степень сохранения p = 0,92) построены зависимости гидравлического сопротивления крупноячеистого и мелкоячеистого ВПЯМ от скорости газового потока. Полученные зависимости согласуются с экспериментальными данными [9]. Установлено, что данная зависимость может быть описана двучленным уравнением вида ΔP(u) = Au2 + Bu, во всём диапазоне скоростей, так как начальный линейный участок, соответствующий ламинарному режиму течения, незначителен.
С помощью зависимости коэффициента гидравлического сопротивления от числа Рейнольдса определено, что турбулизация в слое ВПЯМ начинается при Reкр ≈ 11.
Найдено приближенно значение числа Рейнольдса Re ≈ 250–300, при котором устанавливалось развитое турбулентное течение.
Анализ гидродинамических режимов при фильтрации воздуха через блочные материалы различной структуры показал, что при одинаковой скорости интенсивность турбулентности во ВПЯМ значительно выше, чем внутри каналов материала сотовой структуры, при этом в области скоростей 1–5 м/с для интенсификации массо- и теплообмена рекомендуется использовать крупноячеистый ВПЯМ как наиболее эффективно турбулизирующий поток. Однако гидравлическое сопротивление ВПЯМ в 10–25 раз выше, чем у блочного сотового материала.
Найдены характерные размеры крупных и мелких турбулентных вихрей, данные масштабы различаются в 60–100 раз. С увеличением скорости газа время существования мелких турбулентных вихрей уменьшается.
Работа выполнена при поддержке гос. контракта Министерства образования и науки РФ №16.515.11.5044.
Рецензенты:
Бессарабов А.М., д.т.н., профессор, заведующий учебно-научным комплексом, ФГУП «Государственный научно-исследовательский институт химических реактивов и особо чистых химических веществ «ИРЕА», г. Москва;
Куркина Е.С., д.ф-м.н., ведущий научный сотрудник факультета ВМК МГУ
им. М.В. Ломоносова, г. Москва.
Работа поступила в редакцию 16.10.2012.
Библиографическая ссылка
Митричев И.И., Кольцова Э.М., Женса А.В. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ГАЗОДИНАМИЧЕСКОЙ ОБСТАНОВКИ ВНУТРИ КАНАЛОВ ВЫСОКОПОРИСТОГО ЯЧЕИСТОГО МАТЕРИАЛА // Фундаментальные исследования. – 2012. – № 11-2. – С. 440-446;URL: https://fundamental-research.ru/ru/article/view?id=30554 (дата обращения: 26.04.2024).



