Описание и численное моделирование
По теории волн Эллиотта фондовый рынок изменяется в соответствии с моделью восьмиволнового фрактального цикла: например, при возрастающей тенденции получаем пять волн роста и три волны падения [3, 5–6]. При этом каждая волна состоит из волн меньшей степени, которые также состоят из волн еще более меньшей степени.
Представим восьмиволновую модель Эллиотта в виде процесса Ито с определенными функциями сноса и волатильности [4]:
![]()
![]()
![]()
![]() (1)
(1)
Процесс (1) можно решать при помощи схемы Эйлера [2, 4]:
![]()
При этом чем меньше выбирается Δt, тем точнее будет получаемый выборочный процесс по отношению к истинному.
Для примера рассмотрим следующую модель:
![]()
![]()
![]() (2)
(2)
Уравнение (2) на отрезке [t i–1, t i ] имеет решение:
![]()
![]()
В данном случае каждая волна представляет собой логарифмическое блуждание с заданными сносом и волатильностью. Так как при рассмотрении уровня цен x0 > 0, то в среднем волны с возрастающей тенденцией обладают положительным сносом, а волны с убывающей тенденцией – отрицательным. Выбор логарифмического блуждания в качестве конкретного вида Ито-процесса можно объяснить его простотой при численном моделировании и идентификации параметров, а также наличием такой зависимости во многих системах, в том числе и в экономике.
В качестве примера рассмотрим решение уравнения:
![]() (3)
(3)
где

После генерации нескольких версий процесса (3) методом Эйлера, где для первой волны x0 = 1, а для всех последующих значение x0 равно последнему значению предыдущей волны, было видно, что модель демонстрирует различные ситуации волн Эллиотта: растяжение третьей волны, растяжение пятой волны, модель «неудача» [3] или усечение [5, 6].
Средний процесс для (3) определяется следующим образом:
![]() (4)
(4)
где f(t) определяется так же, как и в случае (3).
В отличие от схемы Эйлера, которая позволяет от заданного значения x0 моделировать эволюцию процесса, для функции (4) на всех интервалах, кроме первого (для первого интервала зададим x0 = 1), необходимо пересчитать значения для x0 по формуле:
![]() (5)
(5)
где T – момент времени, когда заканчивается предыдущая волна, а μ – снос моделируемой волны.
Рассмотрим реальный пример из финансового рынка. В качестве финансового инструмента был выбран фьючерсный контракт на курс евро-доллар США (ED). Данные были взяты за период 11.05.2012-13.06.2012 с интервалом 1 час. Для данных цен по закрытию фьючерса ED была подобрана модель (6)
![]()

 (6)
(6)
Как и в случае с (4), на всех интервалах, следующих за первым, значения для x0 были пересчитаны по формуле (5). Модель (6), так же как и исходные данные фьючерса ED, описывают траекторию восьми волновой модели Эллиотта с преобладающей нисходящей тенденцией.
Идентификация параметров методом максимального правдоподобия
Метод максимального правдоподобия получил большое распространение в практике научных исследований. Данный метод представляет собой эффективный способ идентификации параметров случайного процесса по данным наблюдений при условии, что известен вид законов распределения соответствующих случайных выборок [1].
Расчетные формулы оценок параметров методом максимального правдоподобия для логарифмического блуждания следующие [2]:
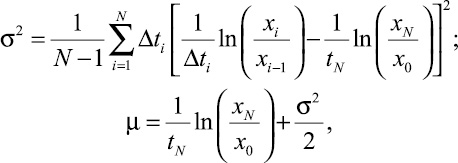 (7)
(7)
где ![]() значения процесса x, регистрируемые в моменты времени
значения процесса x, регистрируемые в моменты времени
![]()
![]()
Проведем численный эксперимент анализа метода максимального правдоподобия для модели логарифмического блуждания.
Алгоритм проведения анализа следующий:
1. Выбор значений параметров сноса и волатильности и длины генерируемого процесса логарифмического блуждания.
2. Генерация 100 версий логарифмического блуждания по схеме Эйлера.
3. Получение оценок параметров методом максимального правдоподобия по каждой из 100 сгенерированных моделей.
4. Вычисление среднего значения и среднеквадратического отклонения по 100 оценкам каждого из параметров.
5. Анализ отклонения средних значений, полученных на шаге 4, от значений, заданных на шаге 1.
Результаты анализа показали, что средние значения оценок параметров имеют тенденцию к занижению при увеличении объема выборки, а среднеквадратическое отклонение постепенно растет. При этом оценки параметров оказались более точными при меньших теоретических значениях параметров (µ = 0,001, σ = 0,0008).
При численной реализации метода максимального правдоподобия для случайных волн Эллиотта на каждом интервале необходимо полагать, что номера наблюдаемых значений начинаются с нуля.
Предположим, что места разрывов кусочно-заданной функции (6) нам заранее известны, тогда с помощью формул (7) можно оценить ее параметры на каждом интервале. При этом предполагаемые длины волн не превышают 58, а теоретические значения параметров, судя по (6), по модулю не превышают 0,0006. Поэтому, основываясь на выше проведенном анализе метода максимального правдоподобия, можно ожидать хороших оценок параметров (8).
При сравнении полученного результата с подобранными параметрами в (6) можно сказать, что оценка функции сноса f(t) оказалась достаточно точной, а оценка функции волатильности g(t) оказалась более завышенной, чем ожидалось. Поэтому в отличие от самого процесса x его средний процесс <x> является достаточно хорошим приближением, который так же точно описывает основную восьмиволновую модель Эллиотта с преобладающей нисходящей тенденцией.
![]()

 (8)
(8)
Тестирование переменной структуры параметров
Для обнаружения точного местонахождения скачка рассмотрим критерий логарифма отношений максимальных правдоподобий, который рассчитывается по следующей формуле:
λ = ln[L(H0)/L(H1)], (9)
где L(H0) – функция максимального правдоподобия, определенная на всем интервале (1, T) для общей модели; L(H1) – функция максимального правдоподобия, определенная в предположении, что на интервале (1, T1) «работает» первая модификация этой модели, а на интервале (T1 + 1, T) – вторая. Точке скачка оценок параметров соответствует максимальное по модулю значение ? среди всех аналогичных значений, рассчитанных для рассматриваемого диапазона.
Функция максимального правдоподобия для марковских процессов определяется выражением:
![]() (10)
(10)
где ![]() – марковская условная плотность распределения вероятностей для момента времени t i .
– марковская условная плотность распределения вероятностей для момента времени t i .
Для логарифмического блуждания условная плотность распределения вероятностей определяется с помощью формулы:
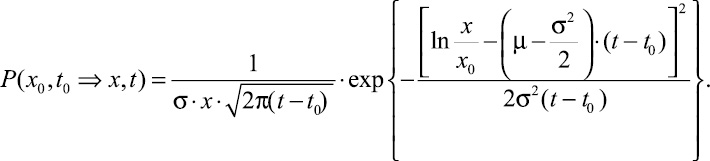 (11)
(11)
Введем обозначение для (11) с учетом параметров:
![]()
Тогда (10) можно записать как:
![]()
Теперь, если положить, что на всем интервале (1, T) используется общая модель с параметрами µ и σ, на интервале (1, T1) модель с параметрами µ1 и σ1, а на интервале (T1 + 1, T) модель с параметрами µ2 и σ2, тогда (9) примет вид:
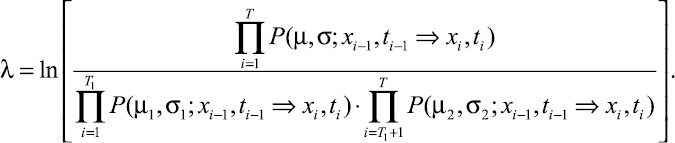 (12)
(12)
После подстановки (11) в (12), (12) можно привести к виду:
![]() (13)
(13)
где функция z определяется выражением:
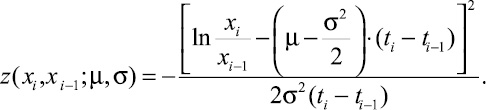
Основываясь на формуле (13), был предложен алгоритм поиска случайных волн Эллиотта, где основными параметрами являются минимальная длина волны и максимальное количество искомых волн. Изменяя эти параметры можно находить волны той или иной степени. При этом результирующий диапазон разрывов должен быть подвергнут интерпретации. Отметим, что в нашей реализации алгоритма мы предлагаем на каждой итерации разбивать волну большей длины, вместо этого можно использовать и другие критерии выбора разбиваемого диапазона. Результат работы алгоритма с параметрами минимальной длиной волны и максимальным количеством искомых волн, равными десяти и восьми соответственно, приведен на следующем рисунке:
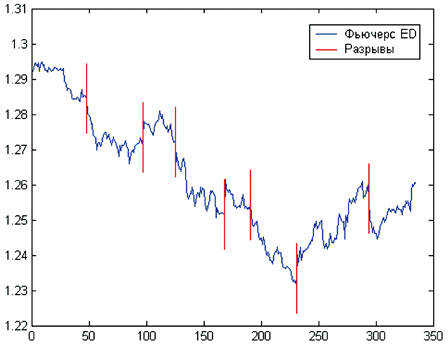
Распознавание случайных волн Эллиотта
Заключение
В данной работе было введено понятие случайных волн Эллиотта и предложена модель, основанная на процессах Ито с кусочно-заданными функциями сноса и волатильности. В качестве конкретного вида Ито-процесса было выбрано логарифмическое блуждание и осуществлено его численное моделирование при помощи схемы Эйлера, а также с помощью точного решения и поправки (5).
Для цен по закрытию фьючерсного контракта на курс евро-доллар США (ED) был предложен процесс, описывающий восьмиволновую модель Эллиотта с преобладающей нисходящей тенденцией.
Был предложен алгоритм анализа метода максимального правдоподобия, позволяющего идентифицировать параметры логарифмического блуждания. Результаты анализа показали, что средние значения оценок параметров имеют тенденцию к занижению при увеличении объема выборки, при этом среднеквадратическое отклонение постепенно растет.
С помощью метода максимального правдоподобия мы осуществили идентификацию параметров модели для фьючерса ED. Результаты идентификации показали, что оценка функции сноса оказалась достаточно хорошей, а оценка функции волатильности получилась завышенной, вследствие чего тенденцию фьючерса ED удобней наблюдать по среднему процессу.
Кроме этого, была выведена расчетная формула (13) для критерия логарифма отношений максимальных правдоподобий в случае модели логарифмического блуждания. Данный критерий позволяет выявлять местонахождения смен одних волн другими. Основываясь на вышеуказанном критерии, был предложен алгоритм автоматического поиска случайных волн Эллиотта в некотором диапазоне с заданными параметрами минимальной длины волны и максимальным количеством волн.
Дальнейшие работы могут быть связаны с анализом использования других видов Ито-процессов при конструировании модели Эллиотта, с анализом методов идентификации параметров, а также с разработкой моделей, основанных на случайных волнах Эллиотта, позволяющих осуществлять прогнозирование.
Библиографическая ссылка
Кесиян Г.А., Уртенов М.Х. СЛУЧАЙНЫЕ ВОЛНЫ ЭЛЛИОТТА // Фундаментальные исследования. – 2012. – № 11-5. – С. 1228-1232;URL: https://fundamental-research.ru/ru/article/view?id=30740 (дата обращения: 26.04.2024).



