Эффективность работы систем электроснабжения в значительной степени зависит от взаимного расположения подстанций и потребителей электрической энергии. Это связано в первую очередь с потерями на передачу электрической энергии и со стоимостью работ по электрификации определенного региона. С другой стороны, эффективность работы электрических сетей зависит от наличия информационных систем и систем управления объектами. Разработка последних определяется правильным проектированием систем электроснабжения.
При проектировании современных систем электроснабжения всегда возникали задачи определения числа, расположения источников питания, распределения приемников электроэнергии по источникам питания [5]. Решать перечисленные задачи становится все сложнее. Это объясняется тем, что проектировщикам приходится оперировать большим количеством исходных данных, объем которых постоянно увеличивается. В первую очередь это относится к возросшему числу приемников электрической энергии. Большой объем данных и постоянный его рост привели к широкому внедрению вычислительной техники в проектную практику, что потребовало разработки иных подходов к проектированию. Первое представление о характере распределения нагрузок по территории объекта получают с помощью картограммы электрических нагрузок [3, 4]. В основе метода лежит принцип определения «центра масс» и используется представление нагрузки в форме равновысоких цилиндров, объем которых пропорционален мощности соответствующей нагрузки. Возможности метода ограничены, так как он позволяет определить место расположения лишь одной подстанции для питания всех потребителей данного региона. Практика проектирования систем электроснабжения показывает, что данная методика не дает однозначного ответа на вопрос оптимального расположения нескольких подстанций, если имеется некоторое количество потребителей, распределенных по площади, но частично сгруппированных. Такая ситуация имеет место в действительности, так как в пределах одной сети электроснабжения имеется ряд центров, вокруг которых и расположены потребители.
Для определения мест расположения нескольких подстанций в одной системе электроснабжения иногда используется метод эквипотенциальных поверхностей [5]. При этом каждой нагрузке, расположенной в некоторой точке, присваивается потенциал, пропорциональный мощности нагрузки. Центром нагрузки в этом случае считается точка с наивысшим потенциалом. Однако действенность такого метода весьма сомнительна, так как превалирующей всегда является нагрузка с максимальной мощностью.
1. Свойство базисной функции
В основу предлагаемого метода определения центров нагрузок для оптимального расположения подстанций предполагается в качестве базисной функции использовать уравнение поверхности:
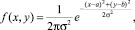 (1)
(1)
где σ – радиус рассеяния значений функции; a и b – координаты вершины поверхности в координатах xy.
Определим объем фигуры, ограниченной поверхностью f(x, y) и плоскостью xy, для чего сначала проинтегрируем исходную функцию по x пределах от –∞до +∞:
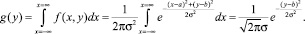 (2)
(2)
Проинтегрируем полученную функцию по y:
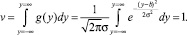 (3)
(3)
Таким образом, объем тела, ограниченного поверхностью f(x, y) и плоскостью xy, равен единице.
При σ = 0 приведенная функция в точке x = a и y = b имеет значение, равное бесконечности, однако объем, ограниченный функцией и плоскостью xy, равен единице. При σ ⇒ ∞ данная функция в точке x = a и y = b имеет значение, стремящееся к нулю, однако объем, ограниченный функцией и плоскостью xy, остается равным единице. При увеличении σ происходит распределение объема по поверхности плоскости xy, объем под поверхностью остается неизменным.
Коэффициент σ является радиусом окружности, образованной точками перегиба поверхности. Это доказывается и тем, что равенство второй производной от базовой функции нулю, дает уравнение окружности с радиусом σ. Поэтому эту величину будем называть радиусом рассеяния.
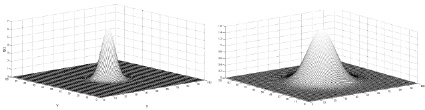
а б
Рис. 1. Изменение формы поверхности в зависимости от значения радиуса рассеяния
На рис. 1 представлена криволинейная поверхность при σ = 10 (рис. 1а) и σ = 20 (рис. 1б). Ордината верхней точки левой поверхности равна примерно шести единицам, а ордината правой поверхности в пять раз меньше. Это объясняется, естественно, тем, что объем фигуры, образованной поверхностью и плоскостью xy, не зависит от радиуса рассеяния.
Таким образом, максимальное значение функции при постоянном объеме фигуры зависит от значения σ: при x = a и y = b,
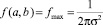
или
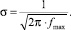
График зависимости σ = p(fmax) приведен на рис. 2. Полученная зависимость в дальнейшем позволит вычислять максимальное значение функции по значению σ и наоборот.
Это свойство функции предлагается использовать для нахождения мест расположения подстанций для питания нагрузок, распределенных по поверхности из условия минимальных затрат на строительство.
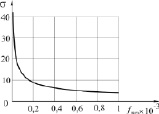
Рис. 2. Зависимость максимального значения функции от радиуса рассеяния
2. Использование базисной функции для представления нагрузок
Каждую нагрузку на поверхности будем представлять фигурами, представляющими собой тела вращения, ограниченные поверхностями, образованными произведением базовой функции на мощность нагрузки. Для потребителя мощностью P и координатами a и b при данном значении σ поверхность описывается уравнением:
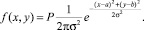
Удельной плотностью мощности будем называть величину, равную среднему значению мощности на единицу поверхности.
Объем тела, ограниченного данной поверхностью и плоскостью xy, будет численно равен мощности. Ранее указывалось на то, что при увеличении σ степень рассеяния мощности по поверхности увеличивается, т.е. удельная мощность в каждой точке поверхности уменьшается.
При большом количестве потребителей объем вычислений, необходимых для нахождения координат подстанции, пропорционально увеличивается. С целью сокращения расчетов отдельные группы потребителей можно заменить одним эквивалентным потребителем, мощность которого равна сумме мощностей приемников. Для этого необходимо определить радиус рассеяния, при котором поверхность трех нагрузок будет практически повторять поверхность одновершинной фигуры. Проведем анализ зависимости ординат вершины поверхности, равной по объему сумме трех нагрузок, от значения радиуса рассеяния σ и высоты «одновершинной» поверхности, объем под которой равен сумме мощностей нагрузки от значения радиуса рассеяния σ.
На рис. 3 кривая 1 представляет собой зависимость высоты поверхности, полученной по предлагаемой выше методике, от радиуса рассеяния. Расстояние между местами расположения нагрузок составляет 20 метров. Кривая 2 представляет зависимость высоты эквивалентной поверхности, объем под которой равен сумме мощностей нагрузки.
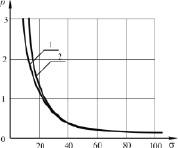
Рис. 3. Зависимость высоты поверхности от радиуса рассеяния
Поведение кривых, представленных на рис. 3, показывает на то, что при радиусе рассеяния, равном примерно 30 метрам, координаты вершин практически равны и отличаются друг от друга не более чем на 10 %. Следовательно, при радиусе рассеяния, равном примерно полутора максимальным расстояниям между потребителями, совокупность потребителей можно заменить одним эквивалентным, мощностью, равной сумме мощностей группируемых потребителей. Значит, при работе с реальными потребителями, распределенными по поверхности определенного региона, для эффективного использования метода необходимо провести анализ нагрузок на предмет плотности их распределения с учетом мощности.
3. Метод определения мест оптимального расположения подстанций
Определение центра масс по известной до настоящего времени теории заключается в вычислении координат центра окружности, площадь которой равна сумме площадей окружностей, представляющих нагрузки с их координатами [2].
Рассмотрим эффективность предлагаемого метода на примере девяти нагрузок. На рис. 4 нагрузки представлены в виде выпуклых неровностей с коэффициентом распределения σ = 6.
При коэффициенте распределения σ = 70 распределение удельной мощности по поверхности меняется. На рис. 5 явно выражены 3 вершины эквивалентных нагрузок, координаты которых определяют центры расположения подстанций.
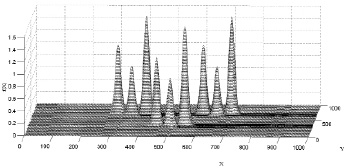
Рис. 4. Представление нагрузок в форме островершинных поверхностей
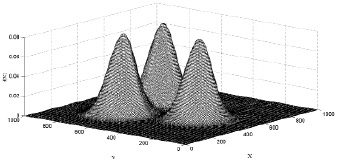
Рис. 5. Процесс образования вершин эквивалентных нагрузок
При необходимости найти место расположения одной подстанции для питания всех потребителей рекомендуется выбрать другой коэффициент распределения, зависящий от степени разброса потребителей.
Очевидно, что представленный способ определения мест расположения подстанций в значительной степени упрощает процедуру вычислений при произвольном количестве потребителей. Метод может быть использован не только для определения оптимальных мест расположения питающих подстанций, но и для решения других задач, связанных с выбором оптимального расположения объектов на поверхности. Для окончательного вывода об эффективности использования метода необходимо провести анализ экономической эффективности количества подстанций.
Предлагаемый подход к выбору оптимальных с точки зрения затрат на строительство мест расположения подстанций является универсальным. Он может быть использован и для определения мест расположения компенсационных установок для сокращения мощности на передачу электрической энергии. Анализ режимов работы реальных разветвленных электрических сетей показывает то, что большое количество электрической энергии теряется на передачу реактивной мощности. Потребителями реактивной мощности являются предприятия с большим количеством станков, в которых используются асинхронные двигатели. К потребителям реактивной мощности относятся и трансформаторы подстанций, работающие в номинальном или недогруженном режиме [1]. Имеется ряд и других потребителей реактивной мощности. Для сокращения потерь, связанных с передачей реактивной мощности, необходимо использовать компенсационные установки. В настоящее время предприятия не заинтересованы в улучшении коэффициента мощности своих потребителей, из-за чего эффективность электроэнергетических сетей снижается. Поэтому единственным решением этой проблемы является установка компенсационных устройств на подстанциях различного уровня. Для того чтобы работа компенсационных установок была эффективной, необходимо на первом этапе определить место установки компенсаторов. И для этого может быть использована предложенная методика. Вторым этапом должна быть разработка автоматических систем регулирования мощности, генерируемой установками.
Однако использование локальных автоматизированных компенсаторов не может преодолеть дефицит генерируемой мощности, так как кроме локальных потребителей реактивной мощности существуют, как было сказано выше, распределенные по сети потребители. Для обеспечения эффективности работы всех компенсирующих устройств сети необходимо разрабатывать систему дистанционного автоматического управления, работа которой основана на анализе распределения реактивных мощностей по сети электроснабжения.
Заключение
Представленный метод определения центров нагрузок эффективен в случае использования средств вычислительной техники. Метод распределенных или удельных нагрузок является теоретической основой построения информационных и управляющих систем электрических цепей. Наилучший результат он обеспечивает при проектировании новых сетей электроснабжения частично сгруппированных потребителей. Для использования этого метода авторами разработана программа, с помощью которой по исходным данным можно быстро получить координаты подстанций для дальнейшего расчета их мощностей проектирования распределительных сетей.
Рецензенты:
Ломтев Е.А., д.т.н., профессор, советник ректора ФГБОУ ВПО «Пензенский государственный университет», г. Пенза;
Мурашкина Т.И., д.т.н., профессор кафедры «Приборостроение» ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.
Работа поступила в редакцию 08.02.2013.
Библиографическая ссылка
Горячев В.Я., Михайлов С.А. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ЦЕНТРА РАСПРЕДЕЛЕННЫХ ПО ПОВЕРХНОСТИ НАГРУЗОК // Фундаментальные исследования. – 2013. – № 4-2. – С. 276-280;URL: https://fundamental-research.ru/ru/article/view?id=31182 (дата обращения: 27.04.2024).



