В настоящее время научная задача обеспечения устойчивости, решаемая в технической, управленческой и других видах деятельности, имеет тенденцию к учёту всё большего количества требований, предъявляемых рядом новых технологий. В техносфере реализовано множество механизмов обеспечения устойчивости систем, но в связи с постоянным развитием искусственных систем инженерам приходится искать новые пути решения гигантской и одной из труднейших научных проблем – проблемы устойчивости технических систем. С точки зрения системного подхода устойчивость возрастает в процессе эволюции систем. Наиболее развитые системы обладают качеством целенаправленности, которое связано с наличием системных механизмов самоорганизации. Подобные адаптивизационные механизмы (усиливающие процесс приспосабливаемости систем к среде) [7] присутствуют в естественных системах высоких уровней развития. Управление в таких системах носит многоцелевой и многопараметрический характер на всех уровнях управления. Такой подход позволяет обеспечивать мультиустойчивость комплексных систем при различных воздействиях внешней среды. В области проектирования искусственных устойчивых систем актуально решение задачи обеспечения адаптивной устойчивости.
В работе авторов [1, 8] определено, что наиболее устойчивыми и развитыми системами из множества адаптивных являются те, которые относятся к метаклассу гомеостатических систем. На основе исследований [8] в данном метаклассе был определён новый класс детерминированных систем управления группового характера развития – класс «Эйкосов», элементы которого представляют собой гомеостатические сети, т.е. используют не одноконтурные рефлексивные механизмы адаптивизации, а связные многоконтурные. За счёт групповой связной многоконтурности система имеет общий целевой запас противоречия, изменение которого повлияет на локальные запасы противоречий. Управление устойчивостью в таких системах реализуется методом стратегирования на основе сценарного подхода, который является эффективным методом прогнозирования комплексной ситуации, а также позволяет определять неожиданные пути решения проблемных задач в сложных системах.
Целью данной работы является генерация новых родов структур гомеостатических сетей в виде конечного множества абстрактных морфологических моделей, входящих в класс «Эйкосов», описанных на основе аппарата теории множеств.
Для достижения поставленной цели выделяются следующие задачи:
– анализ аксиоматики формальной теории систем управления;
– построение и анализ математических моделей гомеостатической сетевой системы;
– определение конечного множества абстрактных гомеостатических сетевых моделей на основе математического аппарата ступеней С.П. Никанорова [4].
Аксиоматика, структуры и признаки гомеостатических систем
В работе [7] представлена аксиома, устанавливающая существование структур гомеостатического типа в причинно-следственной сети управляющих систем, имеющая вид:
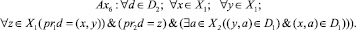
Для данной аксиомы определены следующие элементы: X1 – управляющая система, X2 – объект управления, родовые отношения: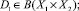 
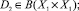pr1d – область определения соответствия [2], pr2 – область значений соответствия [2]. Соответствия [2] определяются в гомеостатической причинно-следственной сети управляющих систем в смысле отображения подмножества x, y множества управляющих систем X1 на подмножество z множества управляющих систем X1 как треугольник управляющих систем. При этом множество всех подмножеств x, y ∈ X1, соответствующих элементу z, называется прообразом z в X1 при соответствии d, а множество всех z ∈ X1, соответствующих элементам x, y, во множестве управляющих систем X1 называется образом x, yв X1 при соответствии d. Функция такого треугольника управляющих систем будет записываться в виде кортежа (f, (x, y), z), а график функции – f ⊆ (x, y)×z. Схематичная трактовка аксиомы представлена на рисунке.
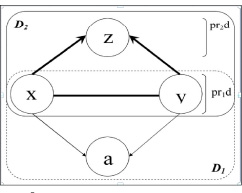
Схема причинно-следственной сети управляющих систем, где x, y, z – подмножества множества управляющих систем, a – подмножество множества объектов управления, D1 – область подмножества множества родовых отношений множеств управляющих систем и объектов управления, D2 – область подмножества множества родовых отношений множеств управляющих систем, pr1d – область определения соответствия, pr2d – область значений соответствия
Таким образом, формальная аксиоматическая теория позволяет определить некоторые подмножества множества трехконтурных управляющих систем как подмножества объектов управления, находящихся под управлением некоторых подмножеств управляющих систем. Описанный сетевой каскад управления определяется в двух основных типах гомеостатической причинно-следственной сети управляющих систем [7]:
1. Рефлексивно-гомеостатическая сеть – сеть гибридной структуры, в которых слой адаптивизирующих (усиливающих процесс приспосабливаемости систем к условиям) подсистем (рефлексивных контуров) располагается вокруг основного гомеостатического контура управления.
2. Гомеостатико-гомеостатическая сеть – сеть, в которых управление множеством гомеостатов осуществляется гомеостатами.
Аксиоматическая формальная теория позволяет формализовать причинно-следственные сети управляющих систем вида «многоэтажных гомеостатов» [7] в качестве простых и хроматических графов, а также гиперграфов [5], что не противоречит известной модели фрактальной организации гомеостатов в функциональные сети [3]. Подобную формализацию можно назвать «структурной» формализацией. Другой вид формализации, «компонентный», позволит определить в причинно-следственной сети управляющих систем компоненты и связи между ними.
Из гомеостатики [3] и медицинской гомеостатики [6] известно шесть базовых гомеостатических структур. Согласно исследованию рассмотрим их как подмножества множества, с выделением принадлежности к субъектной и объектной части системы. Для объекта управления характерны следующие множества гомеостатов [3]: множество компенсационных гомеостатов {КГ} ∈ X2; множество планетарных гомеостатов {ПлГ} ∈ X2; множество пульсирующих гомеостатов {ПГ} ∈ X2; множество ритмических гомеостатов {РГ} ∈ X2. Для системы управления характерны следующие известные [3] множества гомеостатов: множество магнитно-полевых гомеостатов {М – ПГ} ∈ X1; множество информационно-полевых гомеостатов {И – ПГ} ∈ X1. На множестве гомеостатов известны следующие типы отношений [3]: союзнические ⊕ (эффект гомеостатов складывается); партнерские ⊗ (эффект гомеостатов умножается); конкурентные Θ (эффект гомеостатов вычитается).
Для представленных множеств гомеостатов выделяются следующие известные признаки [3], для которых задаются числовые последовательности на основе качественной экспертной оценки, где 1a, 1b и т.д. – качественные оценки:
1) функциональное предназначение (0, 1, 2);
2) уровень качества поддержания гомеостаза (0, 1а, 1b, 1c, 1d, 2a, 2b);
3) сложность структуры (0, 1, 2, 3, 4, 5, 6);
4) жизнеспособность (0, 1, 2, 3, 4, 5, 6);
5) уровень функционирования (0, 1а, 1b, 1c, 1d, 2a, 2b);
6) уровень управления (0, 1, 2);
7) уровень качества подавления проникающей помехи (0, 1а, 1b, 1c, 1d, 2a, 2b);
8) устойчивость антагонистов (0, 1, 2, 3, 4, 5, 6);
9) самокомпенсация (0, 1, 2, 3, 4, 5, 6).
Построение и анализ математических моделей гомеостатической системы
Для «компонентной» формализации требуется построить математическую модель управляющей системы гомеостатического типа в виде теоретико-множественного описания. Для построения математической модели гомеостатической сети введём следующие вспомогательные понятия, используя термины теории множеств [2]: M – множество базовых элементов системы; I – истинное множество элементов; R – множество отношений элементов системы; P – множество свойств элементов системы; C – множество целей системы; Q – множество всех возможных структур системы; Qn – подмножество подходящих структур; F – множество всех возможных функций системы.
Общая теоретико-множественная модель структуры системы имеет следующий вид:
Q = (M, R, ((C ⊂ P) ⊂ F)),
где
♦ множество базовых элементов системы состоит из известных множеств гомеостатов М:{КГ, ПлГ, ПГ, РГ, М – ПГ, И – ПГ};
♦ родовые отношения аксиоматической теории находятся в отношении включения со множеством базовых элементов системы D1, D2 ⊆ M;
♦ множества союзнических, партнерских и конкурентных отношений являются строгими подмножествами множества отношений элементов системы и определяются на всём множестве базовых элементов системы R ⊕ R ⊗ RΘ ⊂ R, где R ⊕ ≠ R ⊗ ≠ RΘ и R ⊆ Mn, где n – число элементов множества базовых элементов системы;
♦ множество целей системы C отображается на множество свойств системы P, отображение которых в свою очередь отображается на множество всех возможных функций системы F.
Используя математический аппарат ступеней [4], получим общую развернутую теоретико-множественную модель системы.
Пусть множество гомеостатов M является универсумом I [2].
I = М:{КГ, ПлГ, ПГ, РГ, М – ПГ, И – ПГ}– множество гомеостатов.
На нормальной ступени S0 определяется сам универсум как конечное разнообразие элементов множества:
S0:I.
На первой нормальной гомоморфной ступени S1 определяется булеан множества (дифференцированное разнообразие групп элементов множества), т.е. определяются 6 групп подмножеств множества, определённые по формальному основанию – числу элементов (0, 1, 2, 3, 4, 5, 6).
S1:B(I).
На второй нормальной гомоморфной ступени S2 определяется декартиан (интегратор разрозненных элементов) булеана множества (разнообразия групп элементов множества) или дифинтеграция разрозненных элементов, т.е. определяются между соседними группами подмножеств множества бинарные отношения. На следующих нормальных гомоморфных ступенях S3–S7 определяется декартиан порядков 2–6 (D2 – D6) булеана множества для определения бинарных отношений для всех элементов внутри множества по типу «все со всеми» (сеть).
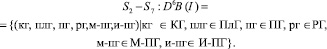
Таким образом, с учётом замены знака операции бинарного отношения «×» декартиана как оператора на операцию отношения, характерную для гомеостатов, в общем виде записываемую как R, и вынесения этой операции за обозначения множества «{}», постулируя такой формой записи наличие множества отношений R на множестве гомеостатов, получаем подмножество абстрактных морфологических моделей гомеостатических сетей по группам подходящих структур систем и определяем соответствующие им наборы экспертных оценок признаков. Для примера приводятся первая и пятая группы из шести:
♦ первая группа:
R{Ø}, {0};
R{КГ}, {1(1), 2(1a), 3(1), 4(1), 5(1a), 6(1), 7(1a), 8(1), 9(1)};
R{ПлГ}, {1(1), 2(1b), 3(2), 4(2), 5(1b), 6(1), 7(1b), 8(2), 9(2)};
R{ПГ}, {1(1), 2(1c), 3(3), 4(3), 5(1c), 6(1), 7(1c), 8(3), 9(3)};
R{РГ}, {1(1), 2(1d), 3(4), 4(4), 5(1d), 6(1), 7(1d), 8(4), 9(4)};
R{М-ПГ}, {1(2), 2(2a), 3(5), 4(5), 5(2a), 6(2), 7(2a), 8(5), 9(5)};
R{И-ПГ}, {1(2), 2(2b), 3(6), 4(6), 5(2b), 6(2), 7(2b), 8(6), 9(6)};
♦ пятая группа:
R{КГ, ПлГ, ПГ, РГ, М-ПГ}, {1(1, 2), 2(1a, 1b, 1c, 1d, 2a), 3(1, 2, 3, 4, 5), 4(1, 2, 3, 4, 5), 5(1a, 1b, 1c, 1d, 2a), 6(1, 2), 7(1a, 1b, 1c, 1d, 2a), 8(1, 2, 3, 4, 5), 9(1, 2, 3, 4, 5)};
R{КГ, ПлГ, ПГ, РГ, И-ПГ}, {1(1, 2), 2(1a, 1b, 1c, 1d, 2b), 3(1, 2, 3, 4, 6), 4(1, 2, 3, 4, 6), 5(1a, 1b, 1c, 1d, 2b), 6(1, 2), 7(1a, 1b, 1c, 1d, 2b), 8(1, 2, 3, 4, 6), 9(1, 2, 3, 4, 6)};
R{КГ, ПлГ, ПГ, М-ПГ, И-ПГ}, {1(1, 2), 2(1a, 1b, 1c, 2a, 2b), 3(1, 2, 3, 5, 6), 4(1, 2, 3, 5, 6), 5(1a, 1b, 1c, 2a, 2b), 6(1, 2), 7(1a, 1b, 1c, 2a, 2b), 8(1, 2, 3, 5, 6), 9(1, 2, 3, 5, 6)};
R{КГ, ПлГ, РГ, М-ПГ, И-ПГ}, {1(1, 2), 2(1a, 1b, 1d, 2a, 2b), 3(1, 2, 4, 5, 6), 4(1, 2, 4, 5, 6), 5(1a, 1b, 1d, 2a, 2b), 6(1, 2), 7(1a, 1b, 1d, 2a, 2b), 8(1, 2, 4, 5, 6), 9(1, 2, 4, 5, 6)};
R{КГ, ПГ, РГ, М-ПГ, И-ПГ}, {1(1, 2), 2(1a, 1c, 1d, 2a, 2b), 3(1, 3, 4, 5, 6), 4(1, 3, 4, 5, 6), 5(1a, 1c, 1d, 2a, 2b), 6(1, 2), 7(1a, 1c, 1d, 2a, 2b), 8(1, 3, 4, 5, 6), 9(1, 3, 4, 5, 6)};
R{ПлГ, ПГ, РГ, М-ПГ, И-ПГ}, {1(1, 2), 2(1b, 1c, 1d, 2a, 2b), 3(2, 3, 4, 5, 6), 4(2, 3, 4, 5, 6), 5(1b, 1c, 1d, 2a, 2b), 6(1, 2), 7(1b, 1c, 1d, 2a, 2b), 8(2, 3, 4, 5, 6), 9(2, 3, 4, 5, 6)}.
На основе результатов использования математического аппарата ступеней (декартиан булеана множества гомеостатов) общая теоретико-множественная модель структуры гомеостатической системы преобразуется в развернутую теоретико-множественную модель системы, имеющую следующий вид:
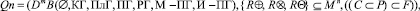
где m – порядок декартиана булеана множества, n – число элементов множества, m = n – 1.
Общая развёрнутая теоретико-множественная модель системы позволяет определить три вида гомеостатических сетей как моделей управления, вытекающих из теории гомеостатики по принадлежности гомеостатов к субъектной и объектной части системы:
– система сетевого гомеостатического объекта управления (SA) – модель объекта управления;
– система сетевого гомеостатического субъекта управления (SB) – модель управляющей системы;
– система сетевых гомеостатических объекта и субъекта управления (SAB = SA ∪ SB) – комбинационная модель системы управления объектом управления.
Выводы
Таким образом, на основе анализа аксиоматической теории адаптивных систем были получены теоретико-множественные модели сетевой гомеостатической системы, позволяющие описать элементный состав, а также комплексную иерархичность и интегративность зависимостей между целями, свойствами и функциями в сети как целостном объекте, что качественно показывает высокий уровень сложности системного управления для обеспечения устойчивости относительно адаптивных систем негомеостатического типа.
С помощью математического аппарата теории ступеней формализован новый класс детерминированных систем управления группового характера развития (класс «Эйкосов») путем синтеза новых родов структур гомеостатических сетей, что характеризует «мощность» и трансдисциплинарную апликабельность данного аппарата как способа получения нового.
Анализ математических моделей позволил определить гомеостатические сети как объекты, субъекты или целостные системы управления, что позволяет соотнести абстрактные морфологические модели, полученные на этапе использования аппарата ступеней, к той или иной группе, что, в свою очередь, повлияет на выбор способов управления в реальных системах, описываемых в рамках кибернетического, а, в частности, гомеостатического, подходов.
Рецензенты:
Камаев В.А., д.т.н., профессор, заведующий кафедрой «САПР и ПК», ФГБОУ ВПО «Волгоградский государственный технический университет», г. Волгоград;
Воронин Ю.Ф., д.т.н., профессор кафедры «САПР и ПК», ФГБОУ ВПО «Волгоградский государственный технический университет», г. Волгоград;
Попов Ф.А., д.т.н., профессор, зам. директора по информационным технологиям Бийского технологического института (филиал) ГОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова», г. Бийск.
Работа поступила в редакцию 03.06.2013.
Библиографическая ссылка
Албегов Е.В., Бутенко Д.В., Бутенко Л.Н. ЭЙКОМОРФОЛОГИЯ. СИНТЕЗ РОДОВ СТРУКТУР ГОМЕОСТАТИЧЕСКИХ СЕТЕЙ // Фундаментальные исследования. – 2013. – № 6-6. – С. 1319-1323;URL: https://fundamental-research.ru/ru/article/view?id=31733 (дата обращения: 24.04.2024).