Известно, что в настоящее время кариозные поражения зубов представляют серьёзную проблему для трудоспособной части населения РФ: почти 90 % оказались подвержены данному заболеванию (см. например [2]). Кариозное поражение зубной эмали проявляется в прогрессирующей деминерализации кристаллов эмали под действием кислот, выделяемых в процессе жизнедеятельности кариесогенных бактерий зубного налета и сопровождается образованием микропор эмали с последующим её разрушением. В результате последовательно развиваются две стадии кариеса: ранняя – стадия кариозного «белого» пятна, и поздняя – стадия образования дефекта (полости) твердых тканей зуба (поверхностный, средний и глубокий кариес). С 2009 года для лечения раннего кариеса все активнее применяется технология Icon (Infiltration CON cept). Суть этой лечебной методики заключается в том, что деминерализованные ткани зуба пропитываются особым светоотверждаемым полимером (фотополимером). До этого поверхность зубов предварительно подвергается специальной обработке кислотой, призванной убрать верхний, наиболее твердый интактый слой эмали и максимально раскрыть ее порозную структуру. Легко-текучий фотополимер, проникая в межкристаллические поры эмали в области кариозного поражения, призван укрепить деминерализованный каркас эмали и усилить прочностные характеристики зуба. Данная методика является неинвазивной, простой в использовании и действительно позволяет эффективно и безболезненно для пациента остановить дальнейшее развитие кариозных процессов. Однако механические прочностные и упругие характеристики такой инфильтрованной порозной эмали к настоящему времени еще недостаточно изучены. В результате до сих пор остается открытым вопрос о том, в какой степени образовавшаяся композитная структура способна заменить прежний интактный слой по прочности, твердости, устойчивости к воздействию агрессивной среды. Проблема осложняется тем, что способы надежного контроля глубины проникновения инфильтранта в межкристаллические поры в клинической практике отсутствуют. У стоматологов еще пока нет и отдаленных (в течение нескольких лет) результатов лечения кариеса данным методом.
В настоящей работе проведено исследование с помощью математического моделирования биохимического процесса развития ранней стадии кариеса, заполнения межкристаллических пор эмали фотополимером, изменения механических свойств зуба после применения технологии ICON. Кроме того, с помощью вычислительного эксперимента изучены изменения упругих свойств зубной эмали, подвергнутой контролируемому разрушающему воздействию (травлению кислотой), вызывающему ее деминерализацию и увеличение пористости, и, напротив, упрочняющему воздействию, происходящему при инфильтрации пор фотополимером ICON.
Моделирование процесса деминерализации эмали зубов
Коронка зуба состоит из 3 частей: внутренняя – пульпа, средняя – дентин и наружная твердая оболочка – эмаль. Её толщина – от 0,1 мм у основания коронки до 2 мм в области жевательной зоны.
Эмаль образована эмалевыми призмами (рис. 1, а), которые радиально поднимаются от более глубокого слоя – дентина. Благодаря своей структуре, эмаль зуба функционирует как «молекулярное сито», а эмалевая жидкость служит переносчиком молекул и ионов. Кислоты, появляющиеся во рту во время приема пищи, проникают в каналы между призмами, вызывают деминерализацию и в конечном итоге могут привести к разрушению зубной ткани (рис. 1, б). В качестве ответной реакции организма активизируется защитная система реминерализации (ЗСР) пульпы, которая снижает кислотность жидкости, находящейся в эмали и, таким образом, уменьшает вредное воздействие кислот, идущих с поверхности зуба вовнутрь [5].
Будем представлять эмаль зуба в виде сплошной пластины толщиной L, имеющей двухслойную структуру, которая равномерно по площади пронизана каналами. С одной стороны, эмаль взаимодействует с внешней средой полости рта, а внутренняя часть зуба (дентин и пульпа) представлена абстрактной областью, в которой может активизироваться ЗСР. Каналам заданы среднестатистические размеры [5] и перпендикулярное к поверхности эмали направление. Принимается допущение об отсутствии сообщения каналов друг с другом, что позволяет нам рассматривать процессы в одном обособленном от остальных канале.
Модель состоит из трёх компонент: канал, заполненный нейтральной жидкостью, и диффундирующие внутрь него кислота и жидкость ЗСР. Канал является осесимметричным и описывается своим радиусом в каждой точке x по всей своей длине [0; L] для любого момента времени t ≥ 0 функцией R = R(t, x). Наличие проникших в канал жидкостей определяется значением функции их объёмных долей φ = φ(t, x) также в каждой точке канала x и в любой момент времени t. Функция объёмной доли кислоты обозначена как φ1, а объёмной доли жидкости ЗСР ‒ как φ2. Взаимореакция компонентов модели происходит без производства продуктов взаимодействия. Кислота и жидкость ЗСР вступают в реакцию, понижая значение своих объёмных долей. Стенки канала (только его боковая поверхность) растворяются под действием кислоты, увеличивая его радиус и, опять же, понижая значение объёмной доли кислоты. Изначально канал имеет форму цилиндра. Проникновение жидкостей в канал происходит с его открытых торцов и описывается граничными условиями. Подробное описание и обоснование математической модели в виде краевой задачи для нестационарных уравнений в частных производных дано в работе [3].
а  б
б 
Рис. 1. а – схематичное изображение выхода эмалевых призм на поверхность зуба; б – кислота зубной бляшки проникает по каналам в эмаль и разрушает её
Выполним обезразмеривание, где в качестве характерных величин берутся: радиуса ‒ начальный радиус поры; для переменной x – длина поры L; времени – характерное время деминерализации. Сделав естественное прдположение, что характерное время диффузии и установления химического равновесия системы кислота-жидкость ЗСР на несколько порядков меньше характерного времени деминерализации, можно получить упрощенную квазистационарную краевую задачу [6]:
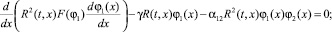 (1)
(1)
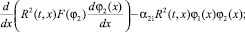 (2)
(2)
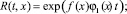 (3)
(3)
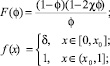 (4)
(4)
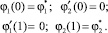 (5)
(5)
Краевая задача (1)–(5) решалась численно методом установления с помощью консервативной неявной разностной схемы [7].
Поскольку реальные значения констант-параметров, входящих в построенную модель неизвестны, обсуждаемые ниже результаты расчётов носят скорее качественный характер и выявляют особенности моделируемого процесса. На рис. 2 представлено распределение радиуса канала в моменты безразмерного времени t = 1, 2, 3, для следующего набора параметров:
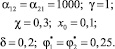 (6)
(6)
В этом случае поверхностный слой в 5 раз более устойчив к воздействию кислоты, чем остальная часть эмали. Из рис. 2 видно, как канал приобретает бутылкообразную форму, и возникает возможность появления крупных пор за счет слияния каналов в самых широких местах. Причем, если считать начальную просветную площадь пористой эмали за 25 %, то при t = 1, 2, 3 её максимум в точке x = 0,1 увеличивается до 34, 45 и 59 % соответственно. Таким образом, деминерализация зуба происходит неравномерно вдоль канала эмали, что связано с неравномерностью концентрации кислоты и свойств зубной ткани.
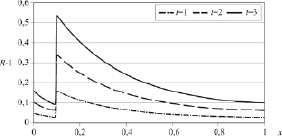
Рис. 2. Распределение радиуса канала вдоль его длины в моменты времени t = 1, 2, 3
Полученные результаты хорошо согласуются с клинической картиной кариеса, когда подповерхностный, менее резистентный к кислоте слой эмали, разрушается быстрее поверхностного слоя с образованием малозаметного белого пятна.
Для выяснения влияния интенсивности реакции нейтрализации на формирование канала были просчитаны три варианта, в которых использовались параметры (6) за исключением значений α12 и α21:
1) α12 = α21 = 1000;
2) α12 = α21 = 100;
3) α12 = α21 = 10.
Во всех трех случаях решение имело вид, аналогичный рис. 2, менялось только значение радиуса в точке x = x0 = 0,1 (максимум) и x = 1 (минимум). В табл. 1 приводятся значения просветной площади (в процентах) при x = x0 = 0,1 для анализируемых вариантов параметров в три момента времени.
Таблица 1
Значение просветной площади ( %)
|
Вариант |
t = 0 |
t = 1 |
t = 2 |
t = 3 |
|
1 |
25,0 |
33,8 |
45,2 |
59,3 |
|
2 |
25,0 |
36,6 |
52,3 |
72,3 |
|
3 |
25,0 |
38,9 |
59,3 |
90,3 |
Откуда видно, что при t = 1 различие результатов для разных вариантов относительно невелико и их можно относить к ранней стадии кариеса. С увеличением времени это различие становится все более существенным и кариес переходит в более развитые стадии.
Моделирование технологии ICON
Технологию ICON можно условно разделить на четыре этапа:
1) удаление поверхностного слоя с помощью химического воздействия;
2) нанесение на поверхность эмали композитного материала;
3) проникновение композитного материала в каналы эмали;
4) затвердевание композитного материала под воздействием света.
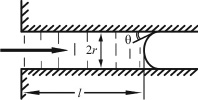
Рис. 3. Перемещение жидкости на длину l в капилляре радиуса r; θ – краевой угол
Рассмотрим модель процесса проникновения композитного материала в каналы эмали. Поскольку размеры каналов от 2 до 5 мкм, основным механизмом такого проникновения являются капиллярные силы. Схематично этот процесс представлен на рис. 3. Скорость v перемещения мениска в тонком вертикальном капилляре, когда влияние силы тяжести мало, определяется уравнением Пуазёйля:
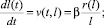 (7)
(7)
где 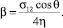
Пусть необходимо заполнить канал длиной L = l(T), тогда из уравнения (7) в простейшем случае R(l) ≡ 1 получаем T0 = L2/(2βr0). С учетом криволинейности стенок капилляра (см. рис. 2), переходя в декартову систему координат, окончательно получаем:
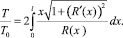 (8)
(8)
В табл. 2 представлены результаты расчетов, полученные для трех вариантов формы канала, (в зависимости от параметров α12 и α21), где t – время окончания кариозного процесса. С учетом того, что начальный радиус каналов r0 = 3,5 ± 1,5 мкм, положив в формуле (8) его среднее значение, получим T0 = T0,cp(1 ± 0,43). Тогда с помощью данных табл. 2 можно рассчитать минимальное и максимальное время процесса заполнения канала для разных вариантов исходных параметров и разного времени t.
Таблица 2
Значение T/T0 для разных вариантов
|
Вариант |
t = 1 |
t = 2 |
t = 3 |
|
1 |
0,952 |
0,926 |
0,910 |
|
2 |
0,899 |
0,827 |
0,771 |
|
3 |
0,839 |
0,716 |
0,617 |
Моделирование упругих свойств зубной эмали
Основываясь на сведениях о зубной эмали, логичнее всего рассматривать её как композитный материал. Тогда призмы будут представлять собой волокно, а межпризменное вещество – матрицу. Призмы и межпризменное вещество имеют свои свойства и геометрию, изменение которых (в процессе кариозного разрушения) влечет за собой изменение жесткости зубной эмали на макроуровне. Говоря языком механики композитных материалов, необходимо определить эффективный модуль композитного материала, зная свойства и геометрию его компонентов. Цель заключается в определении модуля упругости при одноосном растяжении (модуля Юнга). Удобней всего определить интересующие нас свойства на ячейке периодичности композитного материала [1]. Представим эмаль в виде композитного материала с гексагональной упаковкой волокон в матрице и выделим ячейку периодичности материала (рис. 4).
Для определения эффективных свойств материала (модулей Юнга в 3 направлениях) необходимо знать макронапряжения на соответствующих площадках ячейки периодичности и соответствующие деформации. Зная эти величины, можно вычислить эффективный модуль материала в конкретном направлении. Таким образом, для нахождения трех модулей Юнга нам потребуется провести 3 компьютерных эксперимента.
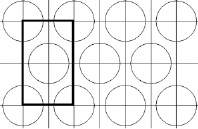
Рис. 4. Структура зубной эмали. Волокно (эмалевые призмы), упакованное в матрицу (межпризменное вещество)
Для проведения численного эксперимента воспользуемся методом конечных элементов. В качестве элемента был выбран 8-узловой гексагон. Зубная эмаль – хрупкий материал, поэтому при его описании ограничивались только упругостью. Кроме того, деформации в рассмотренных задачах не превышают 10 %, что дает возможность использовать линейный закон Гука. Для того чтобы свести к минимуму погрешность, возникающую при изменении объема, необходимо при деформации в одном направлении задать в другом направлении такую же деформацию с противоположным знаком.
В каждом случае мы получаем 3 решения для ячейки периодичности с необходимыми граничными условиями. Однако данные решения не позволяют вычислить эффективный модуль материала. Модуль Юнга находится из эксперимента на одноосное растяжение (сжатие). Вид нагружения в решенных задачах не является одноосным растяжением (сжатием), соответственно он не позволяет найти модуль Юнга.
Для нахождения эффективных модулей пользовались следующим приемом: имея 3 решения линейной задачи, найдем 4-е решение задачи как линейную комбинацию трех других. Далее введем в модель геометрию и свойства кариозного разрушения. Диаметр призм равен приблизительно 5–8 мкм. В рассматриваемой модели радиус призмы принят равным 4 мкм. Расстояние между призмами 10 мкм. Кариозное разрушение начинается с межпризменного вещества. В рассматриваемой модели оно представляет собой цилиндрические включения радиусом 0,5; 1; 1,5 мкм для каждого из трех случаев.
Воспользуемся описанной выше методикой и найдем значения эффективных модулей для эмали, подвергнувшейся кариозному разрушению. ICON применяется только на ранних стадиях кариозного разрушения, поэтому не будем рассматривать дальнейшее увеличение области. К тому же, как показывают исследования, сначала полностью разрушается межпризменное вещество, причем призмы остаются практически не тронутыми.
Следующий этап – оценить влияние ICON на механические свойства зубной эмали. ICON – фотополимер. Будем рассматривать его как изотропный, линейно-упругий материал. Модуль Юнга примем равным меньшему модулю материала призмы и межпризменного вещества, а коэффициент Пуассона – 0,49. Введем ICON в места кариозного разрушения и найдем эффективные модули материала, воспользовавшись описанной выше методикой.
Значения эффективных модулей в направлении X и Y совпадают с точностью до 8 %. Кроме того, значения эффективных модулей находятся между значениями модулей призмы и межпризменного вещества, что согласуется с теорией композитных материалов.
На рис. 5 представлены результаты моделирования, откуда видно, что жесткость эмали ухудшается с увеличением области поражения, что ожидаемо. Применение ICON не только останавливает кариозный процесс с точки зрения диффузии кислоты в зубную эмаль, но и частично восстанавливает жесткостные свойства эмали. Однако, как сказано выше, данные выводы сделаны на основании свойств материала, которые подобраны исходя из соображений здравого смысла.
а 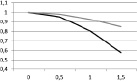 б
б 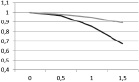 в
в 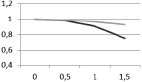
Рис. 5. Безразмерная зависимость эффективного модуля в направлении X(a), Y(б), Z(в) от радиуса области кариозного повреждения (темно-серый – кариозное повреждение, светло-серый – область заполнена ICON)
Чтобы сделать окончательные выводы по этому вопросу, необходимо привлечение данных эксперимента. Учитывая малые размеры объекта исследования, постановка такого эксперимента представляет непростую самостоятельную задачу.
Выводы
На основе имеющихся в настоящее время данных о физиологии человеческих зубов была разработана математическая модель, описывающая эмаль как сплошную двуслойную среду, пронизанную каналами, и основные протекающие в ней процессы (диффузия жидкостей из внешней среды и внутренних слоев зуба; химическое взаимодействие жидкостей и их влияние на эмаль), которая стала основой для математического описания кариозного заболевания. В результате исследования получена информация об эволюции формы каналов эмали в течение развития кариозного повреждения, что позволяет судить об изменении пористости эмали по глубине для любого конкретного момента времени. Анализ результатов показал, что созданные модели правдоподобно отображают особенность исследуемого явления, которая заключается в неравномерности деминерализации эмали. Изменение структуры эмали на микроуровне заключается в том, что её микроканалы, будучи изначально цилиндрическими, приобретают бутылкообразную форму, что сказывается на значении капиллярных сил, а, следовательно, на эффективности инфильтрации композита и лечения в целом. Была получена формула, позволяющая рассчитать минимальное и максимальное время процесса заполнения пор эмали в зависимости от степени поражения эмали кариесом и для различных вариантов исходных параметров.
Разработана методика, позволяющая рассчитывать эффективные жесткостные свойства зубной эмали на ячейке периодичности материала для различной геометрии ячейки периодичности, а также с учетом различных факторов, таких как кариозное повреждение, использование технологии ICON и др. Показано, что технология ICON оказывает положительное влияние не только на сопротивляемость дальнейшему распространению кариозного повреждения, но и на жесткость эмали зуба.
Работа выполнена при поддержке Министерства промышленности, инноваций и науки Пермского края и РФФИ, грант 11-01-96028-р_урал_а, 11-08-96018-р_урал_а.
Рецензенты:
Девяткова Г.И., д.м.н., доцент, заведующая кафедрой общественного здоровья и здравоохранения ФПК и ППС, ФГБОУ ВПО «Пермская государственная медицинская академия имени академика Е.А. Вагнера» Министерства здравоохранения Российской Федерации, г. Пермь;
Пенский О.Г., д.т.н., доцент, профессор кафедры процессов управления и информационной безопасности, Пермский государственный национальный исследовательский университет, г. Пермь.
Работа поступила в редакцию 30.11.2013.



