Образование разреженных потоков является одним из основных процессов при переработке дисперсных материалов [1–5]. В разреженном состоянии осуществляются такие процессы, как смешение, измельчение, ударное разделение суспензий [5] и т.д. Несмотря на такое широкое применение распылительных устройств, практически отсутствуют методики расчета.
Анализ математических моделей, посвященных движению частиц в дисперсных системах (глава 1), показывает наличие двух подходов – одночастичных задач для малоконцентрированных потоков и статистического описания с учетом взаимодействия частиц как с несущей фазой, так и между собой.
Наличие случайных факторов в процессе формирования разреженного потока, таких как неупорядоченность движения частиц, неравномерность распределения их объемной плотности, взаимные и вторичные их столкновения и т.д., требуют вероятностного подхода к решению задачи [1]. При этом основной целью является установление явного вида функции распределения [1] частиц твердой фазы по их диаметрам для энергетически замкнутой макросистемы решением соответствующего кинетического уравнения [1].
Статистическое описание макрофизических систем в их равновесном состоянии, когда выполняется условие энергетической замкнутости, практически эквивалентно описанию стохастического поведения соответствующих им динамических систем [2]. При этом возможен переход от динамических уравнений с учетом ланжевеновских источников к кинематическим уравнениям типа Фоккера-Планка [1] со стационарными решениями в виде функции распределения по набору обобщенных координат макросистемы.
В соответствии со статистическим подходом [1] будем считать, что макрофизические системы разреженных потоков представляют собой равновесные системы не взаимодействующих между собой частиц. Энергия данной системы сохраняется и определяется энергией струи и энергией взаимодействия сформированных частиц с окружающей средой.
Статистическое описание образования разреженного потока частиц выполняется в следующем порядке. Первоначально постулируется распределение числа частиц в элементе фазового пространства, которое определяется совокупностью обобщенных координат макросистемы qυ, т.е. наборам переменных, характеризующих механизм образования разреженного потока. Затем составляется уравнение энергетического баланса в системе «струя-поток», задается условие нормировки для определения неизвестных параметров искомого распределения, выводится выражение для дифференциальной функции распределения числа частиц по обобщенной координате и вычисляются статистические средние как некоторые характеристики поведения дисперсной системы.
В случае образования дисперсной системы потока частиц фазовое пространство определяется совокупностью случайной скорости центра масс частицы dv1 и ее диаметра D1.
Согласно работам [1, 2], для гамильтоновых закрытых систем значение энергии можно считать заданным, и вид канонической функции распределения совпадает с видом равновесной функции, соответствующей принципу максимума энтропии для закрытых макросистем, распределение числа частиц дисперсного потока dN1 в элементе фазового объема ![]() экспоненциально убывает в зависимости от стохастической энергии [1, 2] частицы E1:
экспоненциально убывает в зависимости от стохастической энергии [1, 2] частицы E1:
![]() (1)
(1)
Здесь Е01 – параметр, соответствующий мере энергии частиц, А1 – нормировочный коэффициент.
В общем случае стохастическая энергия частицы состоит из кинетической энергии, энергии взаимодействия с окружающей средой, энергии внутреннего движения, поверхностной энергии и энергии гидродинамического взаимодействия:
![]() . (2)
. (2)
Здесь
![]() (3)
(3)
где σ – коэффициент поверхностного натяжения [3]; φ1 – угол рассеивания, D1 –диаметр частицы, v1 – скорость частицы, H – толщина жидкостного слоя, С – коэффициент гидродинамического сопротивления [2], v – скорость частицы.
Рассмотрим частные случаи образования потоков.
В случае формирования расширяющегося потока твердых частиц в стохастическую энергию входят только первые две составляющих – кинетическая и энергия поперечного движения частиц в потоке (вызванного его расширением) [2, 4]:
![]() (4)
(4)
При распаде одиночных жидких струй на капли стохастическая энергия состоит из кинетической, поверхностной и энергии внутреннего движения [1]:
![]() (5)
(5)
В процессе формирования расширяющейся дисперсных потоков капель также необходимо учесть энергию, затрачиваемую на ее расширение Evz [2, 6]:
![]() (6)
(6)
В выражение для стохастической энергии при формировании потока неоднородных сред, например потока частиц суспензии [7] будут входить все слагаемые.
Следующим этапом моделирования является определение неизвестных констант А1 и Е01, входящих в выражение (1).
Свободный параметр распределения А1 определим из нормировочного соотношения [1], которое отвечает балансу массы в системе «нераспавшаяся струя сформированный поток»:
![]() (7)
(7)
Здесь N1 – полное число частиц, находящихся в потоке в единицу времени.
С учетом (1) выражение (7) примет вид:
![]() (8)
(8)
Неизвестный параметр Е01 в выражении (1), соответствующий мере энергии системы потока частиц [1, 8], находится из уравнения энергетического баланса, составленного для момента формирования разреженного потока:
En = Ep, (9)
где En – энергия нераспавшейся струи (потока), Ep – энергия образованного разреженного потока частиц. Согласно выбранному распределению числа частиц в элементе фазового объема dГ1, можно получить дифференциальные функции распределения числа капель жидкости по углу рассеивания φ1 в фазовом объеме :
![]() (10)
(10)
Дифференциальная функция распределения элементов потока по углам рассеивания φ1 задается выражением :
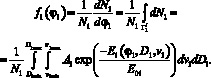 (11)
(11)
Основные средние характеристики процесса распыления, такие как наиболее вероятный угол рассеивания и размер частиц [1], можно определить из следующих выражений:
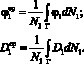 (12)
(12)
Выбор в качестве одной из координат угла рассеивания объясняется тем, что большинство известных диспергирующих устройств создают расширяющиеся потоки, имеющие в поперечном сечении расширяющуюся треугольную (коническую форму).
Таким образом, стохастический подход позволяет получить дифференциальные функции распределения числа частиц по углам рассеивания, а также вычислить средние характеристики процесса образования дисперсных потоков частиц.
Определение максимальной величины угла раскрытия факела
Одним из основных параметров процесса образования дисперсных потоков является угол раскрытия. Величина угла раскрытия факела необходима при расчете параметров распределения A1 и Е01 (выражения (8), (12)). Для определения φ1max была разработана приближенная методика оценки данной величины.
Рассмотрим процесс истечения струи из канала. Согласно многочисленным исследованиям, как теоретическим [1], так и экспериментальным [2], расширение потока происходит в результате обтекания краев канала и взаимодействия с окружающей средой.
Для определения максимального значения угла раскрытия факела составим уравнение энергетического баланса для периферийной части потока, которая подвержена максимальному отклонению от оси потока:
![]() (13)
(13)
Здесь Mc – момент аэродинамических сил; vpx – скорость частиц в конечной части распылителя, определяемая по изложенной в работе [2] методике. Величина момента Mc может быть найдена из выражения
![]() (14)
(14)
где R0 – расстояние от центра распылительного канала до края; Kc – коэффициент лобового сопротивления. Тогда
![]() (15)
(15)
Здесь ξ – коэффициент местного сопротивления [1], учитывающий тип распылителя.
Решая (15) относительно φ1max, имеем:
![]() (16)
(16)
где
![]() (17)
(17)
rootof(õ) – форма представления решения уравнения (16) [9].
Полученные зависимости (16)–(17) могут быть использованы для оценки значения φ1max для потоков, создаваемых канальными устройствами. Величина коэффициента местного сопротивления ξ определяется опытным путем и зависит от типа распылителя.
Рецензенты:Мурашов А.А., д.т.н., заведующий кафедрой математических и естественно-научных дисциплин Московского финансово-юридического университета, г. Ярославль;
Епархин О.М., д.т.н., профессор, директор Ярославского филиала ФГБОУ ВПО «Московский государственный университет путей сообщения, г. Ярославль.
Работа поступила в редакцию 05.12.2013.
Библиографическая ссылка
Лебедев А.Е., Зайцев А.И. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА ОБРАЗОВАНИЯ ДИСПЕРСНЫХ ПОТОКОВ // Фундаментальные исследования. – 2013. – № 10-15. – С. 3338-3341;URL: https://fundamental-research.ru/ru/article/view?id=33062 (дата обращения: 26.04.2024).



