Одним из основных компонентов манипуляционного робота является исполнительная система, в общем случае состоящая из кинематической цепи, двигателей с приводами и механизмов преобразования движения. В зависимости от решаемых задач манипуляционная исполнительная система одного робота может содержать одну или несколько кинематических цепей (манипуляторов), выполняющих одинаковые или различные функции. Например, в многофункциональном лазер-роботе [4] манипуляционная исполнительная система содержит технологический манипулятор, манипулятор оптики и вспомогательный манипулятор, а манипуляционная исполнительная система робота-станка [1] состоит из манипулятора изделия и манипулятора обрабатывающего инструмента. Исполнительные механизмы роботов с несколькими манипуляторами называют механизмами относительного манипулирования. К таким механизмам относят и механизмы роботов с параллельной кинематикой, образующие стационарно замкнутые кинематические цепи. Обобщенно механизмами относительного манипулирования в исполнительных системах роботов следует считать механизмы, состоящие из нескольких замкнутых или разомкнутых кинематических цепей, каждая из которых имеет управляемую или не управляемую, стационарную или не стационарную связь с выходным звеном или рабочим органом. Наличие значительного количества кинематических пар в указанных механизмах позволяет строить специфические алгоритмы и структуры системы управления.
Интегрированные операции, выполняемые манипуляционными роботами в современном высокотехнологичном производстве или экстремальных средах, осуществляются в условиях параметрической и структурной не стационарности состояния позиционных связей и силовых взаимодействий между рабочим органом и объектом работ, отдельными манипуляторами, а также их звеньями. Указанные связи и взаимодействия можно разделить на два уровня [2]: между манипуляторами через кинематические цепи, рабочие инструменты и объекты работ (связи и взаимодействия первого уровня) и между звеньями внутри манипуляторов (связи и взаимодействия второго уровня). Здесь и в дальнейшем будем считать, что силовым является внешнее по отношению к компоненту системы активное и (или) реактивное воздействие, как результат взаимодействия компонентов в процессе работы.
Во время движения позиционная связь и силовое взаимодействие неразрывно связаны, являясь, по сути, позиционно-силовым взаимодействием на втором уровне постоянно, а на первом – в зависимости от положения компонентов системы и выполняемой операции. При этом возможны два варианта движения рассматриваемого компонента манипуляционной системы: движение за счёт стороннего источника энергии и движение за счёт перекачки энергии в процессе позиционно-силового взаимодействия с другим компонентом. Структурное постоянство указанных связей и взаимодействий на определенном этапе движения можно считать фазой их состояния. Отмеченные выше обстоятельства предопределяют реализацию в манипуляционной системе и каждом приводе робота позиционного, силомоментного и комбинированного управления, аналогично органам движения биологических систем, в том числе человека. Техническая реализация такого интегрированного управления не представляет принципиальных сложностей и не требует ощутимых затрат.
При выполнении различных операций в степенях подвижности манипуляционной системы осуществляется управляемое относительное перемещение звеньев исполнительной кинематической цепи, управляемое силомоментное взаимодействие между ними или комбинированное позиционно-силовое управление. В роботах с параллельной кинематикой и механизмами относительного манипулирования могут содержаться не управляемые кинематические пары, предназначенные для обеспечения в кинематической цепи необходимой подвижности, либо пары и степени подвижности с управлением, отключаемым по определенному алгоритму.
Базовой основой манипуляционных исполнительных систем роботов является совокупность попарно соединенных подвижных звеньев, образующих разомкнутые, замкнутые или комбинированные кинематические цепи. В робототехнике используются преимущественно кинематические пары пятого класса; при этом ось поступательной пары направлена вдоль направления относительного перемещения соединяемых звеньев, а ось вращательной пары ортогональна плоскости их относительного поворота.
Исходя из сказанного выше и пренебрегая трением вдоль оси, состояние кинематические пары предлагается условно классифицировать в зависимости от цели управления и вида взаимодействия, создаваемого между соединяемыми звеньями, следующим образом:
• пассивная кинематическая пара (Пк) – пара, обеспечивающая необходимую подвижность кинематической цепи манипуляционной исполнительной системы без создания управляемого позиционного или силомоментного взаимодействия между соединяемыми звеньями вдоль ее оси;
• пассивная силовая кинематическая пара (Пс) – пара, вдоль оси которой целенаправленно создается не управляемое силомоментное взаимодействие между соединяемыми звеньями без управления их относительным положением;
• активная позиционная кинематическая пара (Ап) – пара, в которой реализуется управление относительным перемещением (или скоростью перемещения) соединяемых звеньев без управления силомоментным взаимодействием между ними;
• активная силовая кинематическая пара (Ас) – пара, вдоль оси которой создается управляемое силомоментное взаимодействие между соединяемыми звеньями без управления их относительным положением;
• кинематическая пара с комбинированным управлением [С(х)] – пара, вид управления в которой может изменяться по определенному алгоритму (вплоть до его отключения) в зависимости от выполняемой операции. Здесь х – характеристика состояний управления в паре.
В соответствии с предложенной классификацией каждой фазе состояния позиционных связей и силовых взаимодействий может быть поставлено в соответствие текущее состояние управления в кинематических парах, которое можно считать фазой состояния управления в манипуляционной системе. Тогда каждая j-я фаза состояния управления (j ∈ Ј = {1, …, k}) будет характеризоваться «n»-мерным множеством Ψj = {х1, …, хn}, где k – количество фаз управления, имеющих место в процессе выполнения операции, а n – число кинематических пар в манипуляционной системе. Конечное «k»-мерное множество Φ(k) = {Ψ1, …, Ψk} можно считать пространством состояния управления манипуляционной системой. Переход от одной фазы состояния управления к другой будем называть фазовым переходом. Для полноты представления первой фазой управления в пространстве его состояния следует считать обеспечение положения статического равновесия перед началом движения, а последней – положения равновесия по окончании движения. Фазовый переход состояния управления может осуществляться по алгоритмам, формируемым в пространстве задания в соответствии с управляющей программой, а также состоянием позиционных связей и силовых взаимодействий в рабочей зоне и манипуляционной системе, как показано на рисунке.
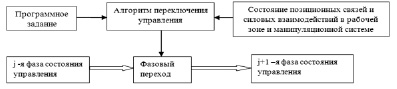
Управление фазовым переходом
Для каждой фазы и пространства управления имеет место соответствие:
Ψj(x) ⇒ Uj(t)m ; Φ(k) ⇒ │U(t)│T, (1)
где Uj(t) – «n»-мерный вектор управляющих воздействий на исполнительные приводы, в общем случае содержащий нулевые компоненты; │U(t)│ – «k×n»-мерный блочный вектор управляющих воздействий, формируемых в процессе выполнения операции.
На основании (1) можно записать операторные выражения для переменных состояния кинематических пар в виде
Qj(р) = WJ(р)·Uj(р) ;
¦Q(р)¦ = ¦W(р)¦·¦U(р)¦. (2)
Здесь Qj(р) – «n»-мерный вектор состояния управляемых и не управляемых кинематических пар для j-й фазы управления; ¦Q(р)¦ – «k×n» – мерный блочный вектор состояния кинематических пар в процессе выполнения операции; WJ(р) и ¦W(р)¦ – передаточные матрицы, определяемые кинематической структурой манипуляционной системы, структурой привода и видом переменной состояния кинематической пары (перемещение, скорость или силомоментное взаимодействие). Для простой разомкнутой кинематической цепи матрицы WJ(р) и ¦W(р)¦ имеют диагональный вид.
Если позиционные связи и силовые взаимодействия, имеющие место в рабочей зоне при выполнении некоторой операции, представить в инерциальной системе координат некоторым «s» – мерным вектором R(t), то задачу построения управления манипуляционной системой робота, выполняющего эту операцию, в общем виде можно формализовать следующим образом:
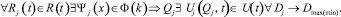 (3)
(3)
Здесь Dj – критерий оптимизации решения задачи для j-й фазы движения.
В манипуляционных системах роботов в зависимости от решаемых задач применяется кинематическое или динамическое управление по относительным или абсолютным координатам, а также по усилию, с которым рабочий орган взаимодействует с объектом работ или комбинированное управление [3].
При кинематическом управлении для заданной траектории или скорости движения рабочего органа (объекта работ) формируется вектор позиционных или скоростных управляющих воздействий на манипуляционную исполнительную систему путем аналитического или итерационного решения обратных задач кинематики:
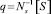 или
или 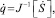 (4)
(4)
где q = q{1, m} – m-мерный вектор обобщенных координат; S = S{1, h} – h-мерный вектор управляемых координат рабочего органа (объекта работ) в инерциальной системе; Ns и J – функциональная матрица и якобиан обратного преобразования.
Как отмечалось выше, первой фазой управления Ψ1 можно считать обеспечение положения статического равновесия (режима «Lock») перед началом движения. Реализация этого режима в степенях подвижности встроенными в безредукторные мехатронные модули электромагнитными тормозными устройствами, с помощью самотормозящихся механических передач или двигателем при «коротком замыкании» в позиционном приводе соответствует состоянию управления в кинематических парах Пс:
Ψ1 = {х∶ х ∈ Пс}; card Ψ1 = n. (5)
Успешность решения уравнений (4) во многом зависит от соотношения между параметрами m и h (hмах = 6). Однозначность решения в пределах цикла или траектории при n = m предопределяет структуру фазы управления Ψ2:
Ψ2 = {х∶ х ∈ Aс}; card Ψ2 = n. (6)
В то же время при движении координаты вектора S могут изменяться произвольным образом; при этом на отдельных участках часть координат может довольно длительное время оставаться постоянной или принимать нулевые значения. Однозначное решение уравнений (4) для этих участков возможно лишь при «замораживании» части степеней подвижности, что соответствует работе их приводов режиме «Lock». В этом случае структура фазы управления Ψ3 будет иметь следующий обобщенный вид:
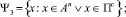 card Ψ3 = n. (7)
card Ψ3 = n. (7)
По окончании движения фаза управления будет иметь структуру, аналогичную Ψ1 (Ψ4 = Ψ1).
Пространство состояний управления в рассмотренном случае при последовательном чередовании фаз представляет собой множество:
Φ(4) = {Ψ1, Ψ2, Ψ3, Ψ4}; card Φ = 4n. (8)
Фазовые переходы в (8) формируются в соответствии с программным заданием, включая разрешение возможных сингулярных состояний.
При n = m фазам управления, характеризуемым множествами (5)–(8), можно поставить в однозначное соответствие векторы обобщенных координат.
При n > m фазы состояния управления манипуляционной системой будут более разнообразными, и для их формирования потребуются дополнительные критерии оптимизации, например, кинематическая точность.
В случаях более сложного динамического управления формирование управляющих моментов приводов может быть выполнено путем компенсации динамических эффектов исполнительной системы в пространстве обобщенных координат и их производных (кинематические пары Ап), либо использованием моментных регуляторов (кинематические пары Ас) [5]. Предполагая наличие в каждом приводе робота позиционной и моментной обратных связей и возможности комбинированного позиционно-силового управления, структурный синтез пространства состояний управления можно рассматривать как задачу построения системы с переменной структурой в зависимости от количественных значений динамических показателей исполнительной системы и требований к ее качеству на различных этапах движения.
Наиболее сложной является задача построения пространства состояний управления при работе с наложенными связями. В этом случае необходимо найти отображения нестационарного шестимерного вектора позиционных связей и шестимерного вектора силовых взаимодействий рабочего инструмента с объектом работ для различных этапов движения (выполнения операции) на пространство обобщенных координат с целью определения его структуры из условия выполнения рабочей операции при минимизации, например, управляющих моментов.
Работа выполнена при финансовой поддержке РФФИ (проект № 13-08-01364)
Рецензенты:Гоц А.Н., д.т.н., профессор кафедры тепловых двигателей и энергетических установок Владимирского государственного университета имени Александра Григорьевича и Николая Григорьевича Столетовых (ВлГУ), г. Владимир;
Кульчицкий А.Р., д.т.н., старший научный сотрудник, главный специалист ООО «Завод инновационных продуктов КТЗ, г. Владимир.
Работа поступила в редакцию 05.12.2013.
Библиографическая ссылка
Умнов В.П., Егоров И.Н. ФОРМИРОВАНИЕ ПРОСТРАНСТВА СОСТОЯНИЙ УПРАВЛЕНИЯ ИСПОЛНИТЕЛЬНЫМИ СИСТЕМАМИ МАНИПУЛЯЦИОННЫХ РОБОТОВ // Фундаментальные исследования. – 2013. – № 10-15. – С. 3419-3422;URL: https://fundamental-research.ru/ru/article/view?id=33078 (дата обращения: 08.05.2024).



