Структурно-базовая технология (СБТ) [5] создания систем коллективного пользования (CKП) [6] предполагает блочность (вложенную), модульность, структурированность и структурную однородность модулей системы на всех уровнях иерархии, что обусловливает стандартность и рекурсивность управляющих процессов, простоту и надежность системы. Эта технология в достаточной мере соответствует естественным структурам сложных объектов автоматизации и обусловливает простоту и естественность реализации свойств коммуникабельности, мультипликативности и параметричности систем баз данных (БД) и баз программ (БП). Она предполагает также использование единых принципов организации структур различных классов (типов) данных и концепции БД при формировании и ведении информационного фонда системы.
Такой подход обусловливает определённое обобщение методов анализа и реорганизации иерархических структур и процессов управления ими. Для этого эффективно может быть использован метод последовательного углубления (МПУ) [4].
Механизм метода последовательного углубления
МПУ рассматривает анализируемую структуру как частично упорядоченное иерархическое множество А, на котором определено некоторое отношение порядка δ из множества ∆ допустимых на этом множестве отношений. Анализ А производится на истинность некоторого предиката р ∈ Р = {рi}. Предикат р0 называют управляющим, рi (i = 1, 2, ..., m) – функциональными. В каждом конкретном случае р0 выбирает рi, истинность которого проверяется. В случае истинности рi выполняется некоторая процедура qj (j = 1, 2, ..., k) из множества процедур Q = {qj}. Процедура q0 управляющая и обеспечивает выбор qj, соответствующего рi.
Пусть 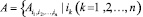
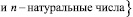 , k – уровень иерархии, n – число уровней иерархии, ik – номер элемента на k-м уровне иерархии. Пусть δ есть отношение порядка на множестве A. Назовём множество элементов k + 1-го уровня, составляющих элемент
, k – уровень иерархии, n – число уровней иерархии, ik – номер элемента на k-м уровне иерархии. Пусть δ есть отношение порядка на множестве A. Назовём множество элементов k + 1-го уровня, составляющих элемент 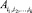 k-го уровня, составляющим множеством этого элемента и обозначим его через
k-го уровня, составляющим множеством этого элемента и обозначим его через 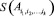 . Будем считать, что количество элементов составляющего множества
. Будем считать, что количество элементов составляющего множества 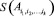 задаётся функцией f(i1, i2, …, ik), а количество элементов на самом верхнем уровне иерархии равно m. Для составного элемента
задаётся функцией f(i1, i2, …, ik), а количество элементов на самом верхнем уровне иерархии равно m. Для составного элемента 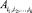 f(i1, i2, …, ik) > 1, а для простого, очевидно, значение функции f равно единице. Тогда механизм метода последовательного углубления состоит в выполнении следующих шагов.
f(i1, i2, …, ik) > 1, а для простого, очевидно, значение функции f равно единице. Тогда механизм метода последовательного углубления состоит в выполнении следующих шагов.
Шаг 1. Для { 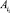 | i1 = 1, 2, …, m; m – натуральное число} выполнить p.
| i1 = 1, 2, …, m; m – натуральное число} выполнить p.
Шаг 2. Для i1 = 1 с шагом 1 до m выполнить: если f(i1) > 1 для {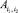 | i2 = 1, 2, …, f(i1)} выполнить P.
| i2 = 1, 2, …, f(i1)} выполнить P.
Шаг 3. Для i1 = 1 с шагом 1 до m выполнить: если f(i1) > 1, для i2 = 1 с шагом 1 до f(i1) выполнить: если f(i1,i2) > 1, для {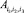 | i3 = 1, 2, …, f(i1, i2)} выполнить p.
| i3 = 1, 2, …, f(i1, i2)} выполнить p.
. . . . . . . . . . . . . .
Шаг n. Для i1 = 1 с шагом 1 до m выполнить: если f(i1) > 1, для i2 = 1 с шагом 1 до f(i1) выполнить: … выполнить: если f(i1, i2, …, in–1) > 1, для {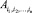 | in = 1, 2, …, f(i1, i2, …, in–1)} выполнить p.
| in = 1, 2, …, f(i1, i2, …, in–1)} выполнить p.
Особенности некоторых применений МПУ
Механизм МПУ позволяет естественным образом составлять простые алгоритмы для многих приложений – для любых иерархических структур. Он, по существу, является схемой алгоритма и превращается в последний, как только будут определены A, ∆, Р и Q. Далее в качестве иллюстрации приведём несколько примеров.
1. Распараллеливание программ [3].
Применение на всех уровнях (структурное, операторное и операционное) структуры программы единого, простого и естественного механизма МПУ позволяет выделять в программе максимальный параллелизм на данном языковом уровне. Т.е. при условии использовании алгоритмов распараллеливания циклов и процедур он позволяет получить полную параллельную форму (ППФ) программы на языке высокого уровня. При этом степень статического параллелизма равна
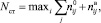
где 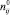 – степень статического параллелизма j-го модуля (множества составляющих операторов) i-го уровня иерархии;
– степень статического параллелизма j-го модуля (множества составляющих операторов) i-го уровня иерархии; 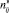 – степень статического параллелизма j-го выражения i-го уровня иерархии;
– степень статического параллелизма j-го выражения i-го уровня иерархии;
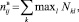
где k – количество выражений в i-м операторе j-го уровня; l – номер уровня иерархии k-гo выражения в i-м операторе j-гo уровня; Nkl – степень параллелизма k-го выражения l-го уровня иерархии.
Заметим, что в эту формулу как частный случай входит также параллелизм (на уровне выражений) операторов последовательных участков программы.
Отметим некоторые особенности как самого МПУ, так и алгоритмов распараллеливания:
– При распараллеливании посредством МПУ сохраняется естественная иерархическая структура исходного множества и отношение порядка между элементами структуры. Вместе с тем формируется другая иерархическая структура, базирующаяся на новом отношении порядка – параллелизме операторов или операций.
– Параллелизм выделяется процедурой q внутри модуля. При этом в каждом модуле выделяется максимальное число минимальных параллельных модулей. Отсюда, естественно, следует максимальный параллелизм, включающий внутримодульный и межмодульный параллелизм.
Возможность выделения максимального параллелизма на данном языковом уровне следует также из теоремы Дильворта [2] и соответствующих методов выделения независимых цепочек.
Частично упорядоченное множество иерархической структуры А будем интерпретировать как иерархическую сеть. Обозначим ni1, ni2 …, nij, число независимости подмножества 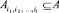 , составляющего элемент
, составляющего элемент 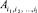 l-го уровня. Тогда имеет место утверждение: минимальное число цепей, покрывающих А, равно
l-го уровня. Тогда имеет место утверждение: минимальное число цепей, покрывающих А, равно
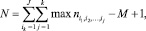
где J – глубина иерархии; М – количество элементов, для каждого из которых число независимости его составляющего множества отлично от нуля.
Вычитаемое М – 1 имеет место, поскольку одна из цепей, покрывающих составляющее множество каждого элемента, является составной частью некоторой цепи верхнего уровня иерархии (за исключением самого верхнего уровня). Очевидно, что приведенное утверждение представляет собой обобщение теоремы Дильворта для иерархических сетей. Задача выделения минимального числа непересекающихся цепей, покрывающих данное частично упорядоченное множество (т.е. числа независимости 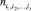 ), может быть сформулирована и решена как задача линейного программирования транспортного типа.
), может быть сформулирована и решена как задача линейного программирования транспортного типа.
– МПУ допускает простое рекурсивное описание его алгоритма. Однако рекурсивность и естественная распараллеливаемость требуют реентерабельности реализующей его программы.
– Возможность использования одних и тех же полей памяти при применении процедуры к различным составляющим множествам повышает экономность и эффективность реализующей программы.
– Механизм МПУ допускает естественное распараллеливание собственного алгоритма. При этом степень параллелизма применения процедуры q равна максимальному числу модулей, расположенных на одном и том же уровне иерархии (исходной структуры), исключается многократное повторение без необходимости значительного числа действий.
– Повышение производительности системы от распараллеливания пропорционально величине 1/(F(1 – F)/N), где F – последовательная часть программы, N – число процессоров.
2. Параллельный синтаксический контроль.
Назовём модулем оператор программы. Операторы, входящие в данный оператор, представляют собой его составляющее множество. Множество модулей данной программы составляет A.
Под отношением δ будем понимать отношение вложенности модулей.
Процедура p выделяет в пределах данного составляющего множества данного уровня множество не вложенных друг в друга модулей, снабжает их соответствующими описаниями (дублирует необходимые для данного блока описания объемлющих блоков) и осуществляет синтаксический контроль модулей данного составляющего множества.
Полученный в результате такой интерпретации алгоритм позволит выделять на каждом уровне минимальные самостоятельно контролируемые модули. Поскольку пооператорный контроль связан с большими затруднениями (в частности, с чрезмерным дублированием описаний), может оказаться целесообразным определить модуль как блок программы.
Заметим также, что использование метода последовательного углубления при синтаксическом контроле программы позволит существенно сократить время синтаксической отладки программы. Такое же замечание можно было бы сделать и относительно общей отладки программы.
3. Анализ, реорганизация и оптимизация систем организационного управления.
Структура организационного управления (напр., регионом, муниципальным образованием, отраслью, отдельным предприятием или организацией и т.д.) может быть представлена как иерархическая система, на разных уровнях которой требуется разный уровень агрегирования информации. Очевидно, используя МПУ, может быть составлена обобщённая схема управления, из которой посредством задания на входе (в процессе настройки системы) значений параметров (типа организационной структуры, условий анализа, реорганизации или оптимизации и процедур их исполнения и др.) в каждом конкретном случае может быть получен соответствующий алгоритм.
Выводы
1. Предикаты P и процедуры Q могут быть сколь угодно сложными. Они могут устанавливать для элементов A, не удовлетворяющих δ, новые типы отношений и строить иерархии, удовлетворяющие этим новым отношениям порядка.
В приведенном выше первом примере устанавливается отношение параллельности между элементами, что позволяет в пределах каждого модуля, а следовательно, и в пределах всего множества установить иерархию в отношении параллельности.
Процедура Q может включать в себя также элементы оптимизации. Однако ни оптимизация, ни установка новых отношений и соответствующих им иерархий не должны нарушать исходного отношения порядка между элементами и соответствующей этому отношению иерархической структуры.
Заметим, что иногда возможно нарушение между некоторыми элементами исходного отношения порядка без нарушения иерархической структуры системы. Например, распараллеливание частично независимых операторов с введением соответствующих средств синхронизации.
В третьем примере условия, отношения и процедуры могут быть чрезвычайно многообразными.
2. Если желательно укрупнение элементов, между которыми устанавливается новое отношение, можно ввести некоторый коэффициент, ограничивающий углубление. Например, в первом примере это может быть некоторый вес в стандартных алгоритмических единицах сложности [1], во втором примере – количество символов (длина конструкции в символах), такое, чтобы каждая формируемая минимальная конструкция, удовлетворяющая новому отношению порядка, имела минимальное из возможных отклонение от этого коэффициента.
3. Кроме такой перспективной области, как параллельное программирование, МПУ может быть использован и в других разделах мультиобработки информации. Он может быть также весьма полезным при организации работы вычислительных сетей и комплексов, сетей вычислительных центров, в области сетевого планирования и управления и т.д. При этом, вероятно, потребуется воспользоваться понятиями мультибаз данных, иерархических сетей и др. и механизмами их реализации.
4. Несмотря на сходство с методом обхода деревьев, МПУ существенно отличают от него возможности ограничения углубления посредством весовых функций и параллельного выполнения процедур Q.
Рецензенты:
Адамадзиев К.Р., д.т.н., профессор, зав. кафедрой информационных технологий и моделирования экономических процессов Дагестанского государственного университета, г. Махачкала;
Курбанмагомедов К.Д., д.т.н., профессор, директор Дагестанского института (филиала) Московского государственного открытого университета, г. Махачкала.
Работа поступила в редакцию 25.12.2013.
Библиографическая ссылка
Халилов А.И. УПРАВЛЕНИЕ ИЕРАРХИЧЕСКИМИ СТРУКТУРАМИ ПОСРЕДСТВОМ МЕТОДА ПОСЛЕДОВАТЕЛЬНОГО УГЛУБЛЕНИЯ // Фундаментальные исследования. – 2013. – № 11-6. – С. 1154-1157;URL: https://fundamental-research.ru/ru/article/view?id=33267 (дата обращения: 26.04.2024).



