Моделирование пограничного слоя атмосферы при помощи CFD пакетов позволяет достаточно точно прогнозировать распространение облаков опасных газов, возникающих в случае аварий на химических опасных объектах. При этом крайне важным является адекватное описание поведения распространения газа в зависимости от устойчивости атмосферы. Следовательно, обязательным условием является корректное задание граничных метеоусловий (профили скорости, температуры, турбулентные характеристики и т.д.), которые потом не будут искажены и изменены по длине расчетной области в процессе численного моделирования. Еще одной сложной задачей является выбор граничных условий для турбулентных характеристик, от которых непосредственно зависит коэффициент турбулентной диффузии, и, следовательно, реальное распределение газа в любой точке атмосферы.
При моделировании распространения облаков опасных газов в атмосфере для учета атмосферной турбулентности на основе вертикального градиента температуры чаще всего применяется классификация по Паскуиллу [2, 4]. При использовании этой классификации профиль температуры задается простейшим линейным уравнением, в котором отсутствует влияние теплового потока от поверхности земли с воздухом.
В качестве других граничных условий турбулентных характеристик, некоторые исследователи использовали значения масштаба и интенсивности турбулентности, которые считали заранее известными [1]. Профиль скорости и параметры турбулентности, используемые в расчетах, определялись методом последовательных приближений, до получения одинаковых профилей по всей длине расчетной области. Такой подход позволяет проводить оценочные расчеты, но не учитывает варианты устойчивости атмосферы в конкретных условиях.
В целом при использовании CFD пакетов необходимо учитывать, что решаемые уравнения не вполне адекватно описывают физику турбулентности в атмосферном пограничном слое. Так, например, наиболее часто применяемые уравнения k–εpsilon модели для замыкания турбулентности (для нахождения турбулентной вязкости) не содержат членов, учитывающих генерацию турбулентности силами плавучести. Различные варианты устойчивости атмосферы (нейтральная, устойчивая, неустойчивая) должны учитываться с помощью различных граничных условий. При моделировании используют масштаб длины Монина ‒ Обухова, абсолютное значение которого определяет высоту, до которой влияние сил трения на турбулентность превышает влияние сил плавучести. При положительном значении этой длины атмосфера считается устойчивой, другими словами, данная ситуация подавляет турбулентность, что должно учитываться в модели. Соответственно, при отрицательном масштабе длины Монина ‒ Обухова атмосфера неустойчива, и данная ситуация должна усиливать турбулентность. Нейтральная атмосфера – это адиабатическая атмосфера без притока тепла извне, то есть с нулевым потоком тепла от поверхности земли. При нейтральной атмосфере масштаб длины Монина – Обухова равен бесконечности, что означает, что влиянием сил плавучести на турбулентность можно пренебречь. Моделирование всех этих трех сценариев в CFD пакетах представляет большую трудность, особенно, когда ставится цель – создание горизонтально-однородного пограничного слоя атмосферы, при котором вертикальные профили всех параметров потока должны сохраняться на протяжении длины порядка нескольких километров, на которой практически происходит рассеивание облаков опасных газов до безопасных для человека концентраций. В литературе предлагались различные подходы для численного моделирования пограничного слоя атмосферы, включая изменение констант турбулентности, использование различных граничных условий для верхней и выходной границы, добавление источниковых членов и т.д. [5–7, 11–13]. Большая часть этих работ была посвящена вопросам моделирования нейтральной и устойчивой атмосферы. Предлагались уравнения как для сжимаемой, так и для несжимаемой среды. При этом важную роль играет выбор того или иного CFD пакета, поскольку решение уравнений, граничные условия, параметры турбулентности (высота шероховатости и т.д.) реализованы в различных CFD пакетах по-разному. Наиболее часто в работах используются пакеты Fluent, CFX и Star CD (или разновидность Star CCM+).
В настоящей работе разработан подход с использованием уравнений для сжимаемой и несжимаемой среды через решение уравнения состояния идеального газа с использованием пакета Fluent 6.3. В модели на верхней границе используется условие Дирихле [9] с известными расчетными значениями всех параметров потока, на входной границе задаются вертикальные профили через применение пользовательских функций (UDF), на нижней границе задается значение температуры для уравнения энергии, а для компонент скорости и турбулентных характеристик используются стандартные пристеночные функции, полученные из логарифмического закона стенки для скорости. На выходной границе используется условие Pressure Outlet [10]. При этом особое внимание уделяется профилю давления, т.к. задание однородного профиля давления на выходе приводит к проблемам со сходимостью и к искажению действительного поля течения под действием силы тяжести.
Физико-математическая модель
Система дифференциальных уравнений, определяющих трехмерный нестационарный поток газовоздушной смеси, перенос энергии, газа, турбулентной кинетической энергии и скорости диссипации турбулентной кинетической энергии, имеет следующий вид [14]:
Уравнение неразрывности:
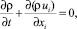 (1)
(1)
где ρ – плотность воздуха или газовоздушной смеси, кг/м3; xi – координаты x, y, z в метрах (x – горизонтальная координата в направлении ветра; y – горизонтальная координата в направлении поперек ветра; z – вертикальная координата); ui – компоненты осредненной скорости ветра u, v, w, м/с.
Уравнение для переноса импульса:
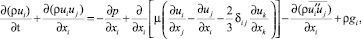 (2)
(2)
где p – давление, Па; 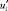 – пульсационные скорости, м/с.
– пульсационные скорости, м/с.
Уравнение для переноса энергии:
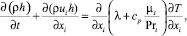 (3)
(3)
а энтальпия, в единицах кДж/кг, равна:
h = cpT, (4)
где cp – удельная теплоемкость при постоянном давлении, кДж/(кг·К); T – температура воздуха, К; λ – коэффициент теплопроводности, Вт/(м·К); Prt – турбулентное число Прандтля; Prt = 0,85.
Уравнение для переноса газа:
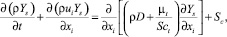 (5)
(5)
где Ys – массовая доля компонента s газовоздушной смеси; Sct – турбулентное число Шмидта; D – коэффициент молекулярной диффузии, зависящий от состава смеси, м2/с; Sc – источниковый член, определяющий генерацию газовой примеси, кг/(м3·с). В случае включения этого уравнения в модель через соответствующую опцию в Fluent («Species Transport on»), во всех уравнениях переноса значения коэффициентов переноса и всех переменных потока будут значениями для смеси, определяемые используемыми по умолчанию правилами для смешения.
Уравнение для переноса k (турбулентной кинетической энергии):
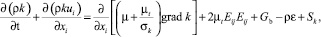 (6)
(6)
где Sk – источниковый член.
Генерация (подавление) турбулентности, обусловленная температурной (плотностной) стратификацией, определяется из выражения [10]:
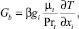 (7)
(7)
где gi – компонент вектора гравитации в i-м направлении, м/с2; β – коэффициент термического расширения, 1/К.
Для идеальных газов уравнение выше приводится к виду
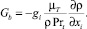 (8)
(8)
Уравнение для переноса ε (скорости диссипации турбулентной кинетической энергии):
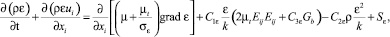 (9)
(9)
где Sε – источниковый член, кг/(м·с4), который здесь принимается равным нулю; тензор Eij определяется стандартными выражениями k–ε модели.
В уравнении (9) имеется связанный с силами плавучести коэффициент С3ε, рассчитанный из следующего соотношения:
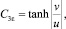 (10)
(10)
где v и u – компоненты вектора скорости газовоздушного потока, м/с, параллельный и перпендикулярный вектору силы тяжести соответственно.
Уравнение для турбулентной вязкости, кг/(м·с):
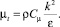 (11)
(11)
Уравнение для коэффициента турбулентной диффузии:
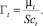 (12)
(12)
Уравнение состояния идеального газа:
ρ = (pраб + p)/(R·T/Mω), (13)
где pраб – рабочее давление, Па; p – избыточное давление, рассчитанное пакетом Fluent, Па; R – универсальная газовая постоянная, Дж/(моль·К); T – температура газа, К; Mω – молекулярный вес газа, г/моль.
Константы турбулентности согласно работам [5–6] допускается принимать
Cμ = 0,0333; σk = 1,00; σε = 1,3;
C1ε = 1,176; C2ε = 1,92.
Данные константы турбулентности в случае моделирования пограничного слоя атмосферы отличаются от констант турбулентности, используемых в Fluent по умолчанию. Результаты расчетов показали, что коэффициенты турбулентной диффузии, полученные при использовании k-ε модели с указанными константами хорошо согласуются с коэффициентами турбулентной диффузии, полученными по данным Монина и Обухова. При этом если принять турбулентное число Шмидта за единицу, то коэффициент турбулентной диффузии, полученный в результате численного моделирования, будет полностью совпадать с коэффициентом Kz, найденным по теории подобия Монина – Обухова [3]:
Kz = (K·u*·z)/(1 + β*·z/L), (14)
где K – константа Кармана (в расчетах использовалось значение 0,41); u* – динамическая скорость, м/с; z – вертикальная координата, м; β* – некоторая универсальная постоянная, подлежащая определению на основе эмпирических данных; L – масштаб длины Монина – Обухова, м.
Уравнения для измененной «стандартной» k–ε модели для несжимаемой среды остаются теми же, за исключением уравнения состояния идеального газа (13). В этом случае оно выглядит уже как
ρ = (pраб)/(R·T/Mω). (15)
В данной работе не рассматривалась модель Буссинеска для плотности, из-за того, что у этой модели есть существенный недостаток: ее нельзя применять в случае больших перепадов температуры по высоте, так как в этом случае линейная аппроксимация не будет удовлетворять приемлемой точности [10].
Отметим также, что, в случае моделирования сжимаемой среды, входные значения профилей турбулентной кинетической энергии и скорости диссипации турбулентной кинетической энергии удается сохранить во всей расчетной области лишь путем их фиксации в пакете Fluent. Но при этом значительно сокращается время расчета. Однако моделирование с фиксацией профилей можно проводить исключительно на ровной поверхности с небольшими элементами шероховатости. В случае же, когда в расчетной сетке имитируется размещение зданий, технологического оборудования или других препятствий, а также при наличии источников, сильно искажающих профиль ветра, фиксирование турбулентных профилей будет приводить к неверным результатам, так как в этом случае не учитывается генерация турбулентности препятствиями.
Моделирование же несжимаемой среды возможно как с фиксацией профилей турбулентных характеристик, так и без фиксации. При этом сохранение профиля атмосферной турбулентной вязкости во всей расчетной области происходит за счет использования в уравнении для переноса кинетической энергии турбулентности k (6) источникового члена [5–6]:
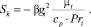 (16)
(16)
Таким образом, применение модели несжимаемой среды без фиксации профилей позволяет учесть изменения турбулентности в случае препятствий. Главное отличие от работ [5–6] состоит в том, что источниковый член (16) используется в случае моделирования несжимаемой среды и при этом источниковый член в уравнении для переноса скорости диссипации кинетической энергии турбулентности ε (9) равен нулю. Благодаря этому затраты машинного времени на выполнение расчетов существенно сокращаются.
Особое внимание при моделировании следует обратить на создание поля давления под действием гравитационных сил земли.
Граничные условия
Моделирование горизонтально-однородного пограничного слоя атмосферы с учетом его стратификации производится до начала выбросов. При этом рассматривался стационарный процесс. Следовательно, в вышеприведенных уравнениях (1–3, 5–6, 9) производные по времени равны нулю; однако в Fluent они используются для получения стационарного решения методом установления по времени.
Для входной (левой) и верхней границ расчетной области использовалось граничное условие «Velocity Inlet», требующее задания значений или профилей всех компонент скорости, температуры, k и ε в соответствии с моделируемым состоянием атмосферной стратификации [3, 5–7, 11–13]:
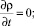
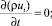
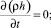 C = 0;
C = 0;
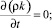
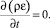
Вход и верхняя граница расчетной области для различных состояний атмосферной стратификации задавались как граничное условие – Velocity Inlet (скорость на входе [3, 5–7, 11–13]):
1. Моделирование неустойчивого состояния атмосферы, L < 0:
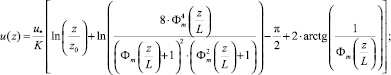 (17)
(17)
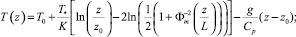 (18)
(18)
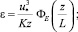 (19)
(19)
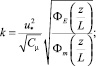 (20)
(20)
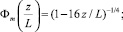 (21)
(21)
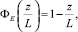 (22)
(22)
где u(z) – скорость ветра на высоте z, м/с; z0 – высота шероховатости, м; 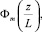
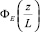 – универсальные безразмерные функции; T(z) – температура на высоте z, К; T0 – температура поверхности (земли), К; T* – масштаб температуры, К; g – ускорение свободного падения, м/с2; ε – скорость диссипации турбулентной кинетической энергии, м2/с3; k – турбулентная кинетическая энергия, м2/с2;
– универсальные безразмерные функции; T(z) – температура на высоте z, К; T0 – температура поверхности (земли), К; T* – масштаб температуры, К; g – ускорение свободного падения, м/с2; ε – скорость диссипации турбулентной кинетической энергии, м2/с3; k – турбулентная кинетическая энергия, м2/с2;
2. Моделирование нейтрального состояния атмосферы, L = ∞:
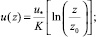 (23)
(23)
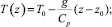 (24)
(24)
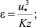 (25)
(25)
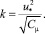 (26)
(26)
3. Моделирование устойчивого состояния атмосферы, L > 0:
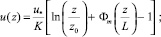 (27)
(27)
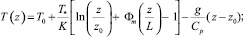 (28)
(28)
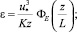 (29)
(29)
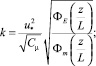 (30)
(30)
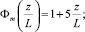 (31)
(31)
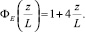 (32)
(32)
При включении уравнения для переноса газа на входной границе необходимо задание массовых долей всех компонентов газо-воздушной смеси.
На нижней границе области задавалось условие прилипания («wall»), подразумевающее, что на этой границе u = v = w = 0. Однако при использовании этой опции в сочетании со стандартной k–ε моделью граничное условие задается не на самой стенке, а в центре первой пристеночной ячейки расчетной сетки через использование логарифмического закона стенки для скорости, температуры и концентрации. Для k и ε задание граничных условий на нижней границе не требуется (для стандартной k–ε модели Fluent использует для k условие ∂k/∂z = 0, а значение ε в центре первой пристеночной ячейки расчетной сетки рассчитывается по стандартной формуле).
Эквивалентная шероховатость:
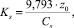 (33)
(33)
где Ks – эквивалентная высота элементов шероховатости на подстилающей поверхности, используемая в Fluent вместо z0 для логарифмического закона стенки, м; Cs – константа шероховатости, Cs = 0,5 [8].
Значение температуры на нижней границе области задавалось постоянным, в соответствии с вертикальным профилем температуры, выбранным для рассматриваемого условия атмосферной стратификации.
На выходной (правой) границе области использовалось граничное условие «Pressure Outlet», требующее задания вертикального профиля давления. При этом градиенты всех остальных переменных потока в нормальном направлении к выходу принимаются равными нулю. В случае возникновения втекания воздуха через эту границу на некоторых итерациях при решении уравнений Fluent рассматривает те участки границы, через которые произошло втекание воздуха, в качестве входной границы. Следовательно, пользователь должен заранее предусмотреть эту ситуацию и задать корректные вертикальные профили для температуры, k и ε на выходной границе для ускорения сходимости решения. Для этой цели в данной работе выходные профили этих переменных потока задавались по тем же зависимостям, что и вертикальные профили на входе.
Отличие от предыдущих работ [5–7, 11–13] заключается в том, что в этих работах на выходной границе использовалось условие либо «Outflow», которое не требует задания вертикального профиля для давления, либо «Pressure Outlet» с заданием однородного вертикального профиля по высоте или с использованием профиля на основе уравнения гидростатики. В данной работе используется условие «Pressure Outlet», но давление задается неоднородным по высоте, когда профиль давления на выходной границе устанавливается неоднородным, через использование опции «Boundary Profile» (граничный профиль). Этот профиль получается итерационным путем. Сначала задается однородный профиль, и расчет ведется до сходимости. Затем записывается профиль из середины области, где профиль давления более-менее установился, и используется в качестве граничного условия на выходе. Затем снова записывается граничное условие из середины области и используется в качестве граничного условия на выходе. Данный итерационный процесс повторяется до тех пор, пока разница между итерациями будет неощутимой.
Расчетная сетка
Описанная выше физико-математическая модель описывает трехмерный процесс. Однако для сокращения времени вычислений в данной работе использовано двухмерное приближение к реальной задаче. Для этого достаточно использования двухмерных конечных элементов для дискретизации расчетной области задачи.
Таким образом, двухмерная расчетная сетка была построена из элементов четырехугольной формы и сгущалась в сторону всех четырех границ области. Размеры области двухмерной расчетной сетки менялись в зависимости от моделирования определённой устойчивости атмосферы в диапазоне от 3000 до 5000 м по длине. Особое внимание было уделено размеру первого ряда ячеек сетки вблизи нижней границы области, т.к. для этого ряда ячеек должно выполняться сразу несколько условий:
1) 30 < y+ < 500;
2) yp > y0.
В расчетах y принималась как координата высоты расчетной области.
Первое условие означает, что центр первой ячейки сетки должен находиться в развитой турбулентной (логарифмической) части турбулентного пограничного слоя атмосферы, имеющего масштаб, приблизительно равный высоте элементов шероховатости на подстилающей поверхности. Второе условие означает, что центр первой ячейки сетки yp должен быть выше элементов шероховатости y0 на подстилающей поверхности [8].
Результаты расчетов
Результаты расчетов приведены на рисунке.
На рисунке представлены результаты численного моделирования в двухмерной расчетной области. В качестве сохраняемых параметров вдоль расчетной области были выбраны: атмосферная турбулентная вязкость, скорость и температура. Вертикальные профили на входной границе x = 0 м строились с учетом теории подобия Монина – Обухова и сравнивались с профилями в сечении x = 500 м при различных стратификациях атмосферы в случаях сжимаемой и несжимаемой сред с учетом фиксации или с учетом использования источникового члена.
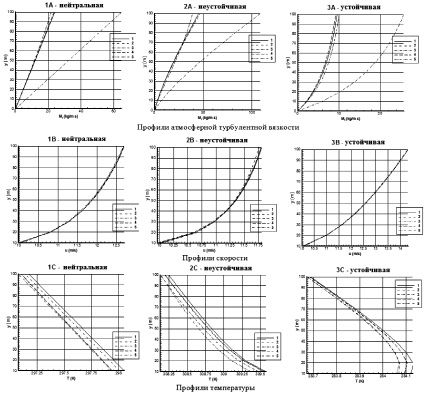
Численное моделирование атмосферного пограничного слоя: 1 – Граничное условие на входе; 2 – Профиль через 500 м, сжимаемая среда, фиксация; 3 – Профиль через 500 м, сжимаемая среда, фиксация, стандартные константы; 4 – Профиль через 500 м, несжимаемая среда, фиксация; 5 – Профиль через 500 м, несжимаемая среда с источником
Согласно результатам численного моделирования лучше всего профили атмосферной турбулентной вязкости сохраняются в случае сжимаемой среды и при фиксации турбулентных характеристик. При этом профили в расчетах с использованием несжимаемой среды отличаются не намного: при использовании фиксации в среднем на 2,7 % от граничных условий на входе, а в случае использования источникового члена на 7,1 %. Лучшее сохранение профилей турбулентной атмосферной вязкости в случае фиксации турбулентных характеристик объясняется малым изменением плотности атмосферного воздуха в ходе моделирования по длине расчетной области, причем в случае сжимаемой среды речь идет о практически полном сохранении входного профиля. При использовании источникового члена профили отличаются не только из-за изменения плотности и влияния, оказываемого самим членом, но еще из-за заданного граничного условия на верхней границе. Для того чтобы снизить влияние граничного условия на верхней границе, необходимо увеличивать расчетную сетку по высоте. В таком случае возможно приемлемое моделирование до такой определенной высоты, когда профиль атмосферной турбулентной вязкости будет не сильно отличаться от входного профиля. Наглядно видно, что использование стандартных констант турбулентности существенно завышает значение атмосферной турбулентной вязкости по сравнению с граничными условиями, полученными по теории подобия Монина – Обухова. Это объясняется тем, что в уравнении (11) для атмосферной турбулентной вязкости стандартная константа турбулентности Cμ принимается равной 0,09.
Профили скорости и профили температуры при разных устойчивостях от граничных заданных условий в среднем отличаются не более чем на 0,1 %.
Тем самым расчеты показали что, несмотря на то, что плотность воздуха в случаях сжимаемой и несжимаемой среды задается различными уравнениями, они не сильно влияют на соответствующие профили скорости и температуры.
Исходя из результатов расчетов, было замечено, что с дальнейшим увеличением продольной координаты x профили начинают отличаться от входного профиля. Для сохранения профилей на еще более дальние расстояния необходимо увеличивать расчетную область в этом направлении. Увеличение сетки в направлении x положительно влияет на сохранение профилей в определенной точке, но увеличивает время расчета.
Такие малые расхождения в профилях атмосферной турбулентной вязкости, скорости и температуры позволяют адекватно учесть распространение опасных газов с учетом стратификации атмосферы во всей расчетной области.
Заключение
Разработанная модель позволяет сохранять входные граничные профили на протяжении всей расчетной области. В частности, сохранение профилей атмосферной турбулентной вязкости во всей расчетной области удалось получить благодаря фиксации профилей в пакете Fluent в случае моделирования сжимаемой и несжимаемой сред, либо путем добавления источникового члена в случае моделирования несжимаемой среды. Зависимость профилей скорости, температуры и турбулентных характеристик от масштаба длины Монина –Обухова, а также возможность сохранения в расчетной зоне всех этих профилей при различных стратификациях атмосферы позволяет адекватно спрогнозировать распространение облаков опасных газов в окружающей среде при различных средах в случае однородного пограничного слоя атмосферы. Использование источникового члена позволяет смоделировать распространение и при наличии препятствий в моделируемой расчетной области.
Рецензенты:
Зиннатуллин Н.Х., д.т.н., профессор кафедры ПАХТ Казанского национального исследовательского технологического университета, г. Казань;
Строганов В.Ф., д.х.н., профессор, зав. кафедрой ХиИЭС Казанского государственного архитектурно-строительного университета, г. Казань.
Работа поступила в редакцию 05.08.2014.
Библиографическая ссылка
Купцов А.И., Акберов Р.Р., Исламхузин Д.Я., Гимранов Ф.М. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПОГРАНИЧНОГО СЛОЯ АТМОСФЕРЫ С УЧЕТОМ ЕЕ СТРАТИФИКАЦИИ // Фундаментальные исследования. 2014. № 9-7. С. 1452-1460;URL: https://fundamental-research.ru/ru/article/view?id=35083 (дата обращения: 05.10.2025).



