Моделирование принципиальной схемы оборудования с применением современных программных решений и вычислительных комплексов существенно упрощает процесс разработки и последующей модернизации оборудования. Применение моделей позволяет рассматривать работу отдельно взятой единицы оборудования как результат взаимодействия функциональных узлов и деталей. При этом становится возможным прогнозировать результат изменения режима работы или характеристик каждого из входящих в состав элементов. Корректность полученной модели зачастую слабо зависит от применяемого программного обеспечения, так как используемые вычислительные пакеты оперируют одним и тем же набором физических законов. Требуемая точность (глубина) вычислений, как правило, настраиваемый параметр, определяющий количество итераций для получения заданной точности. Таким образом, для описанных условий факторами определяющими корректность построенной модели, являются уровень детализации функциональной схемы оборудования и достаточное количество параметров, описывающих текущие характеристики элементов схемы. Данный подход также может быть использован для проведения обратной операции по исследованию характеристик отдельного узла, соответствующих известным режимам работы оборудования. В качестве объектов исследования в таком случае могут выступать модифицированные узлы для уточнения их характеристик, а также узлы, характеристики которых для применяемых режимов работы не известны. Для указанных случаев граничные условия моделирования определяются диапазоном эксплуатационных параметров оборудования.
Данная работа имеет целью определение параметров моделирования вакуумного электронного диода импульсного электронного ускорителя прямого действия АСТРА-М [8]. Ускоритель применяется для разработки радиационных технологий [6, 9] и в научных исследованиях фундаментального и прикладного характера [4, 10] в качестве источника импульсных электронных пучков с параметрами: импульс ускоряющего напряжения до 475 кВ длительностью 500 нс, импульс тока выведенного пучка 0,4 кА длительностью 120 нс, частота следования до 50 импульсов тока пучка в секунду. Исследуемый вакуумный электронный диод является нелинейной нагрузкой для генератора импульсов высокого напряжения в процессе функционирования электронного ускорителя. Принципиальная схема ускорителя [3] не содержит формирующих линий и газовых разрядников повышенного давления – в качестве высоковольтного коммутатора применяется промышленно выпускаемый тиратрон ТДИ1 45/10к, что обеспечивает наработку генератора импульсов ускоряющего напряжения на отказ более 5∙107 импульсов тока пучка в частотном режиме эксплуатации ускорителя. Изучение параметров функционирования генератора на активную нагрузку позволило создать его вычислительную модель [7] с учётом значимых паразитных параметров и характеристик конструктивных элементов. Для создания полной вычислительной модели ускорителя необходимо дополнить существующую модель генератора корректным эквивалентом применяемой нагрузки, в качестве которой выступает вакуумный электронный диод.
Исследование закономерностей изменения импеданса электронного диода с плоскими катодами
Проведённые ранее исследования режимов работы ускорителя [1, 2] позволили определить вольт-амперные характеристики вакуумного электронного диода для разных катодов. На основании полученных ранее данных были выбраны наиболее характерные электрические характеристики электронного диода для разных катодов (рис. 1). Приведённые характеристики получены по результатам измерения ускоряющего напряжения и полного тока диода с помощью ёмкостного делителя напряжения и пояса Роговского соответственно [3, 8]. Мгновенные значения импеданса диода определялись по закону Ома. Для сравнения были выбраны катоды из одинакового материала: многоострийный медный катод из проволоки Ø 0,2 мм и плоские катоды из композиционного материала на основе медной матрицы с включениями керамических частиц Cu + 30Al2O3 и Cu + 50BaTiO3. По результатам предварительных экспериментов, из сравнения исключён плоский катод из меди М0, показавший существенную неоднородность генерации электронного пучка в плоскости сечения (кольцо). Приведённые на рис. 1 кривые получены для катодов равного диаметра (40 мм) при одинаковой величине ускоряющего зазора (20 мм), что обеспечивает идентичную геометрию электронного диода, а следовательно, одинаковую конструктивную ёмкость. Идентичные условия проведения экспериментов при учёте стабильности формирования импульса ускоряющего напряжения 5 % позволяют предположить зависимость полученных кривых импеданса диода преимущественно от эмиссионных характеристик катодов.
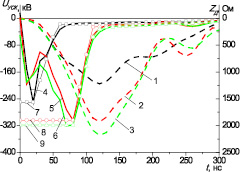
Рис. 1. Характерные кривые импульсов ускоряющего напряжения (1, 2, 3), а также экспериментальные (4, 5, 6) и моделируемые (7, 8, 9) кривые импеданса вакуумного электронного диода с медным многоострийным катодом (1, 4, 7) и композиционными катодами Cu + 30Al2O3 (2, 5, 8) и Cu + 50BaTiO3 (3, 6, 9). Диаметры катодов 40 мм, величина ускоряющего промежутка 20 мм
Анализ формы кривых импеданса позволил выявить схожий характер его изменения за время импульса ускоряющего напряжения. Для последующего моделирования были выделены 4 характерных участка кривой импеданса, которые показаны на рис. 2. Экспериментальное значение импеданса на участке 1 зависит от способа измерения и точности применяемой диагностики, ввиду близких к нулю значений измеряемых величин и выполнения операции деления для построения кривых импеданса. Для упрощения моделирования узла импеданс вакуумного электронного диода был принят постоянным при наибольшем экспериментальном значении импеданса. Данное упрощение характеризует импеданс диода при отсутствии значимого электронного тока ZXX, фактически иллюстрируя режим «холостого хода» генератора ускорителя. Минимальное значение тока диода на данном этапе позволяет минимизировать погрешность, вносимую в модель принятым упрощением.
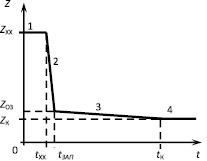
Рис. 2. Моделируемая кривая изменения импеданса вакуумного электронного диода с указанием линейных участков (1, 2, 3, 4) и опорных моделируемых величин: ZXX – импеданс диода «холостого хода»; ZОЗ – импеданс диода при ограничении тока объёмным зарядом; ZК – импеданс диода при окончании импульса ускоряющего напряжения; txx – длительность режима «холостого хода» генератора; tзап – время формирования сплошной плазменной эмиссионной поверхности катода; tк – длительность импульса ускоряющего напряжения.
Поведение импеданса на участке 2 (рис. 2) иллюстрирует существенное увеличение эмиссионного тока через электронный диод и определяется скоростью формирования сплошной плазменной поверхности с учётом максимального тока, ограниченного индуктивностью разрядного контура генератора импульсов ускоряющего напряжения. Точка (tзап; ZОЗ) кривой на рис. 2 соответствует моделируемому моменту формирования сплошной плазменной поверхности с известной площадью. Дальнейшее изменение импеданса вакуумного электронного диода (этап 3) может быть описано законом Чайлда – Ленгмюра [5], с учётом скорости разлёта плазмы. Длительность этапа 3 ограничивается временем действия импульса ускоряющего напряжения tк. Длительность импульса ускоряющего напряжения меньше времени, необходимого для перемыкания ускоряющего промежутка распространяющейся катодной и анодной плазмой, таким образом, конечный импеданс диода представлен постоянной величиной.
Представленная аппроксимация линейными участками реальной кривой импеданса вакуумного электронного диода содержит ряд допущений, упрощающих построение модели диода. Данный подход требует проведения сравнительного анализа величины погрешностей, вносимых предложенными упрощениями. Для выполнения сопоставительного исследования было произведено моделирование работы генератора импульсов ускоряющего напряжения, описанного в [7] на предлагаемую модель вакуумного электронного диода в программной среде моделирования электрических процессов NI Multisim 10.1.1.
Моделирование импеданса вакуумного электронного диода
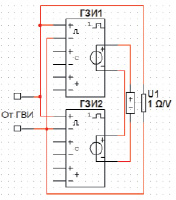
Модель вакуумного электронного диода с нелинейной омической характеристикой, вид которой показан на рис. 2, реализована в виде подсхемы с помощью стандартного инструментария программной среды NI Multisim 10.1.1. Внешний вид подсхемы показан на рис. 3, а. В качестве основного, исполнительного элемента используется управляемый напряжением резистор, с коэффициентом передачи 1 Ом/В.
Для формирования опорного сигнала управляемого резистора были применены два последовательно соединённых генератора задержанных импульсов (ГЗИ1 и ГЗИ2), работающих по схеме управляемого одновибратора. Настраиваемые параметры ГЗИ, показанные на рис. 3, б, обеспечивают создание задержанных импульсов напряжения с регулируемой амплитудой и временем нарастания амплитуды от минимального значения к максимальному (рис. 3, б). Генераторы ГЗИ запускаются параллельно сигналом от модели генератора импульсов ускоряющего напряжения [7] и c заданной задержкой формируют наклонные участки (2 и 3, рис. 2) моделируемой кривой импеданса. Постоянные уровни импеданса (1 и 4, рис. 2) задаются суммарным значением напряжений ГЗИ для каждого участка кривой импеданса. Параметр «затягивание импульса» (рис. 3, б) устанавливается заведомо больше длительности импульса ускоряющего напряжения, нивелируя значимость параметра «время спада».
Описанная модель вакуумного электронного диода позволяет получать кривую изменения импеданса вакуумного электронного диода вида, представленного на рис. 2 в широком диапазоне требуемых параметров.
 а
а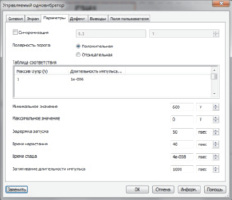 б
б
Рис. 3. Внешний вид подсхемы модели вакуумного электронного диода (а). Окно настройки параметров управляемых одновибраторов ГЗИ1 и ГЗИ2 (б)
Результаты моделирования и их обсуждение
Величина импеданса вакуумного электронного диода определяет баланс энергии в системе генератор – нагрузка, таким образом, в качестве критериев сравнения для определения погрешности предлагаемой модели вакуумного электронного диода были выбраны энергетические характеристики, показывающие скорость передачи энергии в нагрузку (поток энергии) P [МВт] и её переданный объём E [Дж]. Кривые изменения скорости передачи энергии в нагрузку (рис. 4) получены с помощью экспериментальных кривых ускоряющего напряжения, а также экспериментальной и моделируемой кривых импеданса диода.
Отличия полученных экспериментальных и моделируемых кривых потока энергии объясняются принятыми при разработке модели упрощениями. Следует отметить, что принятие значения импеданса постоянной на этапе 1 (рис. 2) практически не привело к внесению погрешности ввиду малых значений регистрируемых сигналов ускоряющего напряжения и полного тока диода. Таблица содержит оценку погрешности моделирования амплитуды скорости передачи энергии из генератора в нагрузку ΔP по сравнению с экспериментальными данными. Полученные результаты моделирования отличаются от экспериментальных на величину не более 6,9 %. Исходя из представленной на рис. 3 и 4 информации, основной вклад в погрешность моделирования вносит аппроксимизация процесса перехода от дискретной к сплошной эмиссионной поверхности катода линейными участками кривой импеданса (участки 2 и 3, рис. 2).
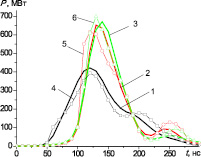
Рис. 4. Характерные кривые потока энергии в вакуумном электронном диоде, полученные экспериментально (1, 2, 3) и при моделировании диода (4, 5, 6) с медным многоострийным катодом (1, 4) и композиционными катодами Cu + 30Al2O3 (2, 5) и Cu + 50BaTiO3 (3, 6)
Так же, для оценки погрешности, вносимой упрощениями, было вычислено интегральное значение энергии E = ʃP(t)dt, переданной генератором в вакуумный диод (нагрузку). Результаты вычислений и оценка отклонения ΔE указаны в таблице.
Оценка погрешности моделирования энергетических характеристик диода
|
Тип катода |
P, МВт |
P*, МВт |
ΔP, % |
E, Дж |
E*, Дж |
ΔE, % |
|
медный многоострийный |
419 |
392 |
–6,9 |
43,38 |
42,14 |
–2,9 |
|
плоский Cu + 30Al2O3 |
652 |
610 |
–6,9 |
45,84 |
48,20 |
4,9 |
|
плоский Cu + 50BaTiO3 |
670 |
698 |
4,0 |
46,68 |
48,1 |
2,9 |
Примечание. * – величина, полученная с применением результатов моделирования.
Погрешность в значении переданной в нагрузку энергии при моделировании не превышает 4,9 %, что сравнимо с точностью применяемого диагностического оборудования.
Заключение
Предложенная модель описания импеданса вакуумного электронного диода может быть успешно реализована стандартными средствами программной среды моделирования электрических процессов NI Multisim 10.1.1. Модель может быть гибко настроена под характеристики существующих диодов с различными катодами, а также использоваться для определения параметров работы генераторов высоковольтных импульсов для не исследованных ранее режимов. Результаты моделирования интегральных энергетических характеристик диодов отличаются от полученных экспериментальным путём на величину менее 7 % для исследованных типов катодов, что позволяет применять предложенную модель для разработки и модернизации существующих генераторов высоковольтных импульсов, работающих на нелинейную нагрузку.
Рецензенты:
Лопатин В.В., д.ф.-м.н., профессор, Институт физики высоких технологий, Национальный исследовательский Томский политехнический университет, г. Томск;
Ремнёв Г.Е., д.т.н., профессор, Институт физики высоких технологий, Национальный исследовательский Томский политехнический университет, г. Томск.
Работа поступила в редакцию 26.08.2014.
Библиографическая ссылка
Егоров И.С., Ежов В.В., Полосков А.В. ИССЛЕДОВАНИЕ ЗАКОНОМЕРНОСТЕЙ ИЗМЕНЕНИЯ ИМПЕДАНСА ЭЛЕКТРОННОГО ДИОДА С ПЛОСКИМИ КАТОДАМИ // Фундаментальные исследования. – 2014. – № 9-9. – С. 1964-1968;URL: https://fundamental-research.ru/ru/article/view?id=35170 (дата обращения: 26.04.2024).



