В современном мире большинство организаций и учреждений в своей работе активно используют каналы передачи информации с большими пропускными способностями. Этими техническими возможностями пользуются и субъекты-нарушители, нанося значительный финансовый ущерб и осуществляя кражу конфиденциальной информации. Поэтому разработка и исследование моделей защиты от распространения вредоносных программ с учетом специфики самих вирусов и компьютерных систем является актуальной научной задачей. Многие математические модели базируются на классических моделях эпидемиологии, так как они наиболее адекватно описывают процесс распространения компьютерных вирусов [3, 6–8]. Формализация данных моделей может быть представлена в виде задачи оптимального управления, которая характеризуется наличием стоимостных оценок эпидемии. Ниже рассмотрим одну из таких задач с учетом времени задержки при инфицировании, с помощью которой описывается особенность вируса – компьютер не может заражать другие машины, пока он не будет инфицирован окончательно [3].
Построение модели. Для формирования модели рассмотрим классическую SIR модель [8], при этом используем следующие предположения [3, 6–8]:
- процесс погашения эпидемии компьютерного вируса рассматриваем на фиксированном промежутке времени;
- вирус размножается по сети с постоянной скоростью без участия пользователя, и повторное заражение узла одним и тем же вирусом невозможно;
- все компьютеры в сети находятся в одном из трех состояний: восприимчивые к заражению, инфицированные и восстановленные;
- общее количество компьютеров является переменным числом с определенной скоростью прироста;
- вредоносная программа имеет латентный период, когда узел инфицирован, но сам вирус не распространяет;
- в сети происходит отключение компьютеров, не связанное с эпидемией;
- за счет установки антивирусного программного обеспечения или межсетевых экранов происходит иммунизация и лечение компьютеров от вируса;
- существует период времени, когда вирус обнаружен и для него разрабатывается патч;
- с постоянной частотой невосприимчивый узел с установленным антивирусом переходит в класс уязвимых при появлении нового вида вредоносной программы.
Исходя из вышеперечисленных предположений, получаем управляемую систему дифференциальных уравнений с постоянным запаздыванием
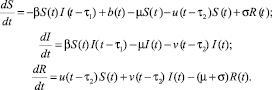 (1)
(1)
При этом
N(t) = S(t) + I(t) + R(t),
где t ∈ [0, T], T – фиксировано.
Начальные условия определены соотношениями
S(θ) = S0(θ) ≥ 0; I(θ) = I0(θ) ≥ 0;
R(θ) = R0(θ) ≥ 0, θ ∈ [–τ, 0]; (2)
u(θ) = u0(θ) ≥ 0;
v(θ) = v0(θ) ≥ 0, θ ∈ [–τ, 0]. (3)
Здесь S0(•), I0(•), R0(•) – непрерывные функции; u0(•), v0(•) – кусочно-непрерывные функции, 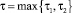 .
.
В системе (1) использованы следующие переменные и постоянные величины. Кусочно-гладкие на отрезке [0, T] фазовые функции S(t), I(t) и R(t) – количество восприимчивых к заражению компьютеров, инфицированных компьютеров и «обезвреженных» компьютеров соответственно. β – коэффициент, характеризующий скорость распространения копии вредоносной программы; b(t) – скорость прироста новых уязвимых узлов; μ – коэффициент, характеризующий постоянную скорость отключения компьютеров, несвязанное с эпидемией; σ – частота заражения новым видом вируса; τ1 = const – время «инкубационного периода», в течение которого узел считается зараженным, но не рассылает копии вирусного программного обеспечения. Кусочно-непрерывные на отрезке [0, T] функции управления v(t) и u(t) характеризуют среднюю скорость восстановления инфицированных компьютеров и установки антивирусного программного обеспечения или межсетевых экранов для восприимчивых узлов. τ2 = const – время обновления антивирусных баз. N(t) – общее количество компьютеров в сети в момент времени t. Заметим, что все вышеописанные параметры и функции модели неотрицательны.
Функции управления v(t) и u(t) почти всюду на [0, Т] удовлетворяют системе неравенств:
u(t) ≥ 0; v(t) ≥ 0, 0 ≤ u(t) + v(t) ≤ U. (4)
Здесь U – максимальная норма управления, которая характеризуется техническими и финансовыми ограничениями.
Для оценки защищенности компьютерной сети будем использовать критерий, который учитывает стоимость нанесенного ущерба и расходы на установку антивируса, а также требование, что в конечный момент времени рассматриваемого периода большинство компьютеров (от 80 до 90 %) являются невосприимчивым к заражению. В результате задача управления будет состоять в минимизации функционала, представленного интегральным и терминальными слагаемыми
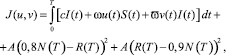 (5)
(5)
где с – относительная стоимость урона, нанесенного одной единицей инфицированного компьютера; ω – средняя стоимость установки антивирусного программного обеспечения или межсетевых экранов; ϖ – средняя стоимость лечения инфицированного компьютера. N(t) = S(t) + I(t) + R(t) – общее количество компьютеров в сети в конечный момент времени, А > 0 – штрафной параметр.
Исследование устойчивости системы [4, 5]. Устойчивость точек равновесия динамической системы является важным фактором при исследовании развития эпидемии. Если существует асимптотически устойчивое положение равновесия, то широкое распространение вредоносного компьютерного кода можно остановить и вернуть систему в нормальное функционирование. В противном случае эпидемия развивается лавинообразно и около 95 % хостов будут инфицированы вирусом. Исследуем систему (1) на устойчивость при постоянных управлениях. Пусть u(t) = u = const ∈ [0, U] и v(t) = v = const∈ [0, U], для всех t ∈ [0, T], удовлетворяющие условию u + v ≤ U. И предположим, что функция скорости подключения новых узлов постоянна, т.е. b(t) = b > 0.
Из классической теории биологической эпидемиологии известно, что существуют два типа положения равновесия: когда отсутствует заражение в системе (I = 0) и эндемическое равновесие (I > 0).
Рассмотрим сначала систему (1) без запаздывания (τ1 = 0). Введем обозначения x = (S, I, R) и приравняем правые части дифференциальных уравнений (1) к нулю. Решая систему, получаем, что на отрезке [0, T] существуют два нетривиальных положительных стационарных состояния:
1) свободное от заражения равновесие –
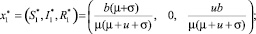
2) эпидемиологическое равновесие –
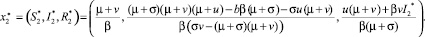
Для анализа устойчивости полученного положения равновесия нелинейной системы используем метод Ляпунова по первому приближению [4]. Для этого линеаризуем систему (1) в окрестности стационарного состояния
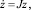
где 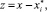 i = 1, 2,
i = 1, 2,
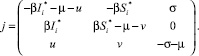
Собственные числа матрицы J являются решениями характеристического уравнения третьего порядка
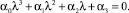
Здесь постоянные коэффициенты αi, i = 1, 2, 3, определены следующими выражениями.
1) для точки 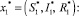 α0 = 1 > 0,
α0 = 1 > 0,
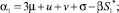
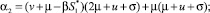
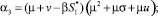
2) для точки 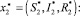 α0 = 1 > 0,
α0 = 1 > 0,
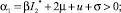
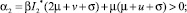
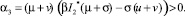
Используем критерий Рауса – Гурвица необходимых и достаточных условий устойчивости. Если α0 = 1 > 0, α1 > 0, α2 > 0, α3 > 0 и α1α2 – α3 > 0, то все корни характеристического уравнения имеют отрицательные действительные части. Тогда, система (1) при нулевом запаздывании будет асимптотически устойчива [4]. Исследуя полученные выше коэффициенты характеристического уравнения, получаем, что точка 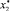 удовлетворяет условиям критерия Рауса – Гурвица. Точка
удовлетворяет условиям критерия Рауса – Гурвица. Точка 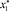 будет удовлетворять критериям устойчивости, если будет выполнено условие
будет удовлетворять критериям устойчивости, если будет выполнено условие
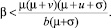
При малом положительном запаздывании, τ1 > 0, выводы о качественном поведении решения системы (1) остаются прежними, но с увеличением величины запаздывания устойчивость положения равновесия x* может быть потеряна [5]. Для исследования в этом случае можно применить второй метод Ляпунова.
Необходимые условия оптимальности [1, 2]. Функция Понтрягина задачи (1)–(5) имеет вид (рассматриваем регулярный случай)
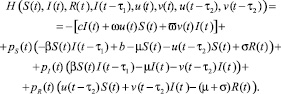
Для удобства в дальнейшем будем использовать следующие обозначения:
Y = I(t – τ1), q = u(t – τ2), g = v(t – τ2).
Теорема 2. [2]. Пусть
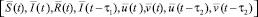 –
–
локально-оптимальный допустимый процесс в задаче (1)–(5), существуют кусочно непрерывно дифференцируемые функции 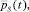
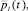
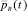 , при которых выполнены
, при которых выполнены
1) принцип максимума Понтрягина оптимальности управления в точках непрерывности
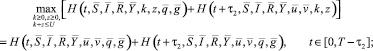 (6)
(6)
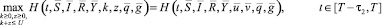 ;
;
2) уравнения Эйлера
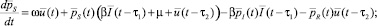
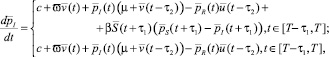 (7)
(7)
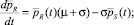
3) условия трансверсальности
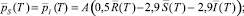
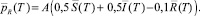 (8)
(8)
Из условия теоремы (6) получаем следующие задачи максимизации:
при t ∈ [0, T – τ2]
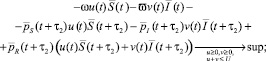
при t ∈ [0, T – τ2]
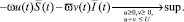
Так как функции управления входят линейно в функцию Понтрягина, то выпишем функции переключения для двух случаев.
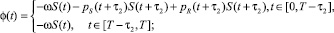
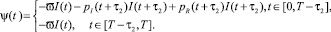
Из анализа задач максимизации и условий (4) находим оптимальное управление
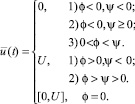
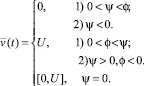 (9)
(9)
Если φ = ψ, то оптимальное управление будет иметь вид
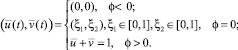
В результате получаем краевую задачу принципа максимума, состоящую из системы дифференциальных уравнений (1), (7) и краевых условий (2), (8), где оптимальное управление определяется из условия (9).
Заключение
В статье была разработана математическая модель управления защитой компьютерной сети от распространения вирусов, с учетом временных параметров, характеризующих время обновления антивирусных баз и время латентного периода вредоносной программы. Представленная модель является достаточно гибкой и универсальной, так как учитываются различные характеристики, которые могут соответствовать конкретным компьютерным вирусам. Построенная модель была формализована как задача оптимального управления с постоянным запаздыванием в фазовой функции и в управлении. Данная задача была исследована на устойчивость. Найдено асимптотически устойчивое положение равновесия системы при малых значениях запаздывания. В виде принципа максимума Понтрягина выписаны необходимые условия оптимальности, с помощью которых определяется оптимальное управление в явном виде. Используя численные методы поиска оптимального решения, можно построить алгоритмическое и программное обеспечение. Это позволит оценить распространение возможной эпидемии, изучить динамику численности зараженных узлов и исследовать эффективность мер противодействия распространению вредоносного кода.
Рецензенты:
Болодурина И.П., д.т.н., профессор, заведующая кафедрой прикладной математики, Оренбургский государственный университет, г. Оренбург;
Попов В.Н., д.ф.-м.н., доцент, заведующий кафедрой математики Института математики, информационных и космических технологий, САФУ им. М.В. Ломоносова, г. Архангельск.
Работа поступила в редакцию 26.08.2014.
Библиографическая ссылка
Семыкина Н.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЗАЩИТЫ КОМПЬЮТЕРНОЙ СЕТИ ОТ ВИРУСА С ПОСЛЕДСТВИЕМ // Фундаментальные исследования. – 2014. – № 9-9. – С. 1982-1987;URL: https://fundamental-research.ru/ru/article/view?id=35173 (дата обращения: 26.04.2024).



