Проблема повышения эффективности управления регионом ставит перед экономической наукой задачу адекватного описания и оценивания социально-экономических показателей регионов, информация о которых может быть представлена в количественном и качественном выражении. Системы и структуры социально-экономических показателей, предлагаемые различными исследователями для оценки социально-экономического положения региона, весьма разнообразны – от нескольких обобщенных, охватывающих лишь самые существенные стороны жизни, до многоуровневых детальных систем, включающих подробнейшие перечисления различных факторов и компонентов. Несмотря на высокий интерес со стороны ученых, вопросы создания и утверждения комплексной системы показателей для исследования социально-экономического положения региона, единой методики, а также методов оценки до сих пор остаются дискуссионным. В связи с изложенной проблемой авторами предлагается использовать комплексный подход к оценке качества жизни населения, основанный на применении динамических нечетких множеств [6] и систем нечетких правил. Такие системы позволяют работать одновременно с качественными и количественными характеристиками, изменяющимися во времени, что необходимо для учета подвижной природы социально-экономических параметров.
Министерство экономического развития РФ разработало методику комплексной оценки уровня социально-экономического развития субъектов РФ, которая утверждена Постановлением Правительства РФ от 11.10.2001 № 717 «О Федеральной целевой программе «Сокращение различий в социально-экономическом развитии регионов Российской Федерации (2002–2010 гг. и до 2015 г.)».
Интегральный показатель развития определяется по следующим нормированным показателям развития субъектов Российской Федерации [5]:
1) валовой региональный продукт на душу населения (тыс. рублей), определяемый как отношение валового регионального продукта к численности населения, деленное на коэффициент уровня покупательной способности;
2) объем инвестиций в основной капитал на душу населения (тыс. рублей), определяемый как отношение объема инвестиций за счет средств всех источников финансирования к численности населения, деленное на коэффициент удорожания капитальных затрат;
3) показатель финансовой обеспеченности на душу населения на основе показателей финансового баланса (тыс. рублей), определяемый как отношение показателя финансовой обеспеченности субъекта Российской Федерации к численности населения;
4) соотношение среднедушевых денежных доходов и величины прожиточного минимума (в процентах);
5) доля населения с денежными доходами ниже величины прожиточного минимума в общей численности населения (в процентах), по данным Федеральной службы государственной статистики;
6) площадь жилищ, приходящаяся в среднем на одного жителя (кв. метров), по данным Федеральной службы государственной статистики;
7) обеспеченность местами детей, находящихся в дошкольных учреждениях (мест на 1 тыс. детей дошкольного возраста);
8) обеспеченность школами – доля учащихся, обучающихся во 2-ю и 3-ю смену (в процентах), по данным Федеральной службы государственной статистики;
9) выпуск специалистов высшими и государственными средними учебными заведениями (специалистов на 10 тыс. человек населения);
10) обеспеченность населения врачами и средним медицинским персоналом (на 10 тыс. человек населения);
11) обеспеченность населения амбулаторно-поликлиническими учреждениями (посещений в смену на 10 тыс. человек населения), по данным Федеральной службы государственной статистики.
Кроме перечисленных выше, авторами было решено использовать дополнительные социально-экономические показатели из статистических сборников Федеральной службы государственной статистики:
12) число зарегистрированных преступлений на 100 000 чел. населения;
13) уровень безработицы;
14) ожидаемая продолжительность жизни при рождении;
15) уровень экономической активности населения;
16) разница между среднедушевыми денежными доходами населения и потребительскими расходами в среднем на душу населения;
17) ввод в действие жилых домов на 1000 человек населения.
Все эти характеристики имеют количественное значение. Однако анализируется, как правило, не само по себе число зарегистрированных преступлений или объем инвестиций в основной капитал на душу населения, а их отношение к значениям аналогичных показателей других регионов или временных периодов. Кроме того, на основе множества показателей вычисляется интегральная оценка уровня социально-экономического развития региона, методики создания которой могут быть различны [1, 3].
Авторами данной статьи предлагается методика моделирования социально-экономических показателей региона и их взаимосвязей, основанная на использовании динамических нечетких множеств и нечеткого вывода. Системы нечеткого вывода предназначены для преобразования значений входных переменных процесса управления в выходные переменные на основе использования нечетких правил продукций. Для этого системы нечеткого вывода должны содержать базу правил нечетких продукций и реализовывать нечеткий вывод заключений на основе посылок или условий, представленных в форме нечетких лингвистических высказываний.
Любое правило состоит из посылок и заключения. Возможно наличие нескольких посылок в правиле, в этом случае они объединяются посредством логических связок И, ИЛИ.
В общем виде это записывается так: R: если x есть A, то y есть B, где «x есть A» – нечеткое высказывание, называемое предпосылкой, а «y есть B» – нечеткое высказывание, называемое следствием правила.
Лингвистическое правило R может быть интерпретировано как нечеткое следствие (импликация) A → B и, следовательно, выражено в виде нечеткого соответствия предпосылки и следствия R = A → B, заданного на декартовом произведении областей определения (четких множествах) входной переменной X и выходной переменной Y.
Композиционное правило вывода выходного значения системы для правила R при входе A′ в записи «x есть A′» определяется как нечеткое множество В′, получаемое с помощью композиции входа и нечеткого соответствия импликации B′ = A′ ○ (A → B).
Для получения нечеткого соответствия
R = A×B, R(x, y) = A(x) → B(y),
где A(x) = μA(x) – значение функции принадлежности элемента x нечеткому множеству A, в приложениях наиболее часто используется импликация Мамдани [2] (т.е. A(x) → B(y) = min{A(x), B(y)}) и max-min композиции. В этом случае значение функции принадлежности выходного нечеткого множества определяется по формуле
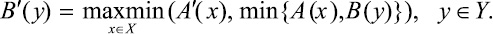
Перейдем к формированию правил для определения уровня социально-экономического развития региона. Для оценки используем перечисленные выше 17 показателей, для которых обозначим лингвистические переменные F1 – F17 соответственно, и интегральный IL. Для каждого показателя (включая интегральный) формируется лингвистическая переменная и область её определения. Число подмножеств устанавливается экспертом. Совокупность значений лингвистической переменной составляет терм-множество этой переменной. Область определения лингвистической переменной для каждого выбранного показателя для оценки будет различной.
Определим терм-множество значений лингвистической переменной
«Уровень показателя Fi» Т = {Низкий уровень показателя; Уровень показателя ниже среднего; Средний уровень показателя; Уровень показателя выше среднего; Высокий уровень показателя} = {VN, N, Z, P, VP},
где VN – very negative; N – negative; Z – zero; P – positive; VP – very positive. Например, область определения лингвистической переменной для показателя «Уровень безработицы» будет выглядеть следующим образом (рис. 1).
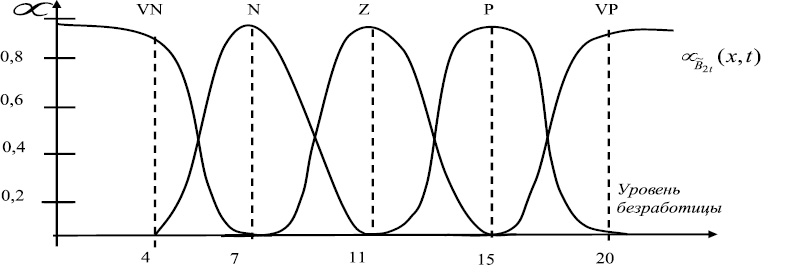
Рис. 1. Функция принадлежности лингвистической переменной «Уровень безработицы»
Уровень социально-экономического развития региона будет выражаться лингвистической переменной IL
«Уровень развития», терм-множество значений которой составлено следующим образом:
Т = {Низкий; Ниже среднего; Удовлетворительный; Выше среднего; Высокий}.
Множество правил нечётких продукций составляют продукционную нечёткую систему, которая может быть записана в виде структурированного текста:
Правило 1: ЕСЛИ «Антецедент № 1», ТО «Консеквент № 1»
…
Правило N: ЕСЛИ «Антецедент № N», ТО «Консеквент № N»
Процесс нечеткого вывода реализуется в соответствии с алгоритмом Мамдани [2], в котором антецеденты ядер правил нечеткой продукции построены при помощи логических связок «И», а консеквенты ядер правил простые. Формализация экспертных знаний о правилах вывода в этом случае может быть осуществлена в виде реляционной таблицы, полями которой являются входные лингвистические переменные – F1 – F17 и выходная интегральная IL. Каждая строка таблицы представляет собой правило (рис. 2).
Антецедент правила состоит из набора значений входных лингвистических переменных, связанных логической операцией «И», причем пустые ячейки таблицы означают, что значения соответствующих им параметров в формировании данного правила не участвуют. Консеквент представлен значением интегральной лингвистической переменной «Уровень развития». Приведенное на рис. 2 правило неформально можно описать следующим образом:
Правило 1: ЕСЛИ «валовой региональный продукт на душу населения имеет высокий уровень» И «соотношение среднедушевых денежных доходов и величины прожиточного минимума имеет уровень выше среднего» И «доля населения с денежными доходами ниже величины прожиточного минимума в общей численности населения имеет низкий уровень» И «площадь жилищ, приходящаяся в среднем на одного жителя, имеет удовлетворительный уровень» И «обеспеченность местами детей, находящихся в дошкольных учреждениях, имеет уровень выше среднего» И «обеспеченность школами имеет уровень выше среднего» И «число зарегистрированных преступлений имеет низкий уровень» И «уровень безработицы имеет удовлетворительный уровень» И «отношение среднедушевых денежных доходов населения к потребительским расходам в среднем на душу населения имеет высокий уровень» И «ввод в действие жилых домов на 1000 человек населения имеет уровень выше среднего» ТО «Уровень социально-экономического развития региона имеет уровень выше среднего».
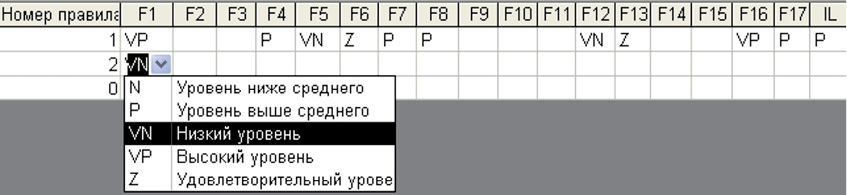
Рис. 2. Таблица правил
Формализация описаний терм-множеств лингвистических переменных также происходит посредством реляционных таблиц (рис. 3). Кроме самих кодовых и текстовых обозначений в таблице приведены соответствующие им трапециевидные функции принадлежности, представленные четырьмя точками (a, b, c, d).
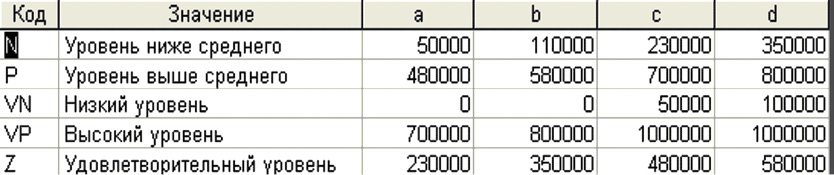
Рис. 3. Таблица терм-множества переменной «Валовой региональный продукт на душу населения»
Выбор трапецеидального вида функции принадлежности (рис. 4) основан на сравнительной простоте вычисления данного вида функций, а также возможности интерполяции с их помощью большинства распространенных функций принадлежности, таких как треугольные и колоколообразные, с достаточной для большинства задач точностью.
Значения функции принадлежности µ(х) могут быть взяты только из априорных знаний, интуиции (опыта) экспертов, которые, в свою очередь, способны достаточно уверенно количественно охарактеризовать границы допустимых значений оцениваемых показателей, чему графически соответствует нижнее основание трапеции {a, d}. Сложнее определить точки горизонтальной части трапеции, интервал между которыми (верхнее основание {b, c,} должен соответствовать полной уверенности эксперта в правильности своей классификации.
Сама природа нечетких множеств и расплывчатость тех понятий и высказываний, которыми оперирует эксперт, подразумевает, что он не всегда может однозначно указать тот интервал значений оцениваемого показателя, в границах которого степень принадлежности нечеткому множеству абсолютна. В связи с этим целесообразно использовать функции принадлежности типа, близкого к колоколообразному, со сглаженными краями верхнего основания (см. рис. 1), где величина интервала абсолютной принадлежности гораздо меньше, чем при построении трапециевидных функций принадлежности. Задача формирования терм-множеств значений лингвистических переменных социально-экономических показателей решена с помощью специально разработанных программных средств [7].
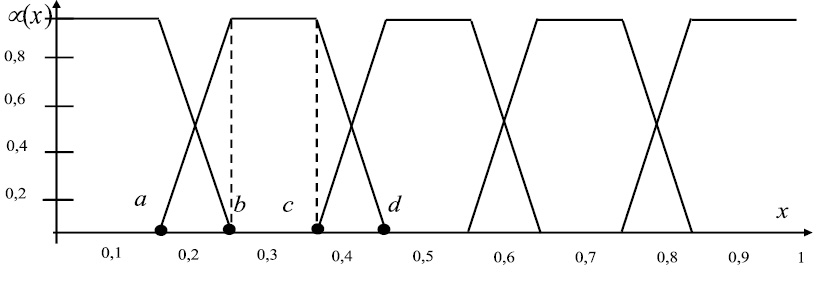
Рис. 4. Функция принадлежности трапецеидального вида
Исследование выполнено при финансовой поддержке РГНФ в проекте проведения научных исследований «Динамическое нечеткое моделирование социально-экономических показателей региона», проект № 14-12-34010.
Рецензенты:Рогачев А.Ф., д.т.н., профессор, заведующий кафедрой «Математическое моделирование и информатика», Волгоградский государственный аграрный университет, г. Волгоград;
Терелянский П.В., д.э.н., доцент, заведующий кафедрой «Информационные системы в экономике», Волгоградский государственный технический университет, г. Волгоград.
Работа поступила в редакцию 26.11.2014.
Библиографическая ссылка
Егорова И.Е., Костикова А.В. ФОРМАЛИЗАЦИЯ ПРОЦЕССА ЭКСПЕРТНОГО ОЦЕНИВАНИЯ ПРИ ДИНАМИЧЕСКОМ НЕЧЕТКОМ МОДЕЛИРОВАНИИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ РЕГИОНА И ИХ ВЗАИМОСВЯЗЕЙ // Фундаментальные исследования. – 2014. – № 11-11. – С. 2476-2480;URL: https://fundamental-research.ru/ru/article/view?id=35969 (дата обращения: 26.04.2024).



