В настоящее время представляется актуальным создание инструментальных средств, обеспечивающих разработку программных сред для доступа предметных специалистов к высокопроизводительным вычислительным ресурсам и использования этих ресурсов без необходимости углубленного знания вычислительных архитектур и низкоуровневых средств разработки приложений [6, 7, 8, 10]. Одновременно прослеживаются тенденции, с одной стороны, использования сервис-ориентированного подхода, подразумевающего организацию сервисов доступа к вычислительным ресурсам посредством сети интернет, с другой стороны, применения мультиагентных технологий для управления вычислениями [3, 5, 11]. Также в последние годы активно ведутся исследования, связанные с привлечением высокопроизводительных вычислений для решения задачи выполнимости булевых ограничений (SAT) – одной из фундаментальных проблем математической логики и теории вычислений. Эта задача состоит в том, чтобы определить, выполнима ли данная булева формула, представленная в конъюнктивной нормальной форме (КНФ), то есть существует ли набор булевых значений переменных формулы, при котором ее значение становится истинным. Известно, что многие практически важные задачи могут быть сформулированы как задачи булевой выполнимости (решения системы булевых уравнений). Высокая вычислительная сложность SAT-задач актуализирует разработку новых эффективных методов и параллельных программных средств их решения, в частности SAT-решателей. В зависимости от реализуемого подхода современные параллельные SAT-решатели делятся на два семейства – решатели, использующие кооперацию и конкуренцию. При первом подходе поисковое пространство делится на части, затем организуется поиск параллельно в каждой части пространства отдельным решателем. При втором подходе каждый решатель работает с одной и той же формулой, но использует альтернативные пути поиска.
Целью данного исследования является разработка алгоритма параллельного решения SAT-задач специального вида в гетерогенной распределенной вычислительной системе (РВС), позволяющего, в отличие от известных (см., например, [13, 14]), учитывать вычислительные характеристики узлов этой системы при динамическом распределении подзадач, полученных в результате расщепления исходной задачи. Новизной предложенного подхода является использование мультиагентных технологий для организации трехуровневого параллелизма процесса решения задачи на основе гибридного подхода с применением MPI и OpenMP. В статье рассматривается мультиагентная система (МАС) HpcSoMas [2, 4], управляющая распределенным решением SAT-задачи на уровне РВС, и гибридный решатель hpcsat [1], предназначенный для решения SAT-задач на вычислительных кластерах с SMP-узлами и использующий на уровне кластера первый подход, с возможностью применения второго подхода на нижнем уровне, в узле кластера.
Мультиагентная система. МАС HpcSoMas предназначена для организации вычислительных экспериментов в предметных областях, где используются дискретные модели в виде систем булевых уравнений. HpcSoMas была разработана на основе сервис-ориентированной технологии, использование которой позволяет реализовать агентов в виде web-сервисов. При дальнейшем изложении материала будем называть сервисы, реализованные на основе архитектурного стиля REST, rest-сервисами, на основе стандарта SOAP – soap-сервисами. В МАС можно выделить три уровня иерархии агентов: уровень пользовательских агентов, представленный клиентами в браузере; уровень агентов-менеджеров (rest-сервисов); уровень реактивных агентов выполнения заданий (soap-сервисов). Многоуровневая архитектура позволяет реализовывать функциональные части МАС по отдельности и при необходимости повторно использовать эти части в других приложениях.
Пользователь может подключаться к агенту-менеджеру через web-интерфейс пользовательского агента, доступный для компьютеров и мобильных устройств, подключенных к сети Интернет, при наличии соответствующей учетной записи пользователя на вычислительном кластере. Все основные функции агента-менеджера вынесены в отдельные soap-сервисы, что позволяет производить замену отдельных компонентов системы либо подключение новых без ее полного обновления. Soap-сервисы могут выполнять следующие функции: расчета ставок на выполнение задания, уведомления пользователей, постановки задания в очередь системы управления заданиями (СУПЗ) вычислительного кластера (ВК), получения информации о состоянии ВК, декомпозиции заданий, расчета оценки состояния ВК, аутентификации пользователей и др. Sat-решатель так же представлен, как soap-сервис, с помощью разработанных авторами средств оформления приложения пользователя в виде сервиса [2].
С помощью web-интерфейса пользователь формулирует постановку задачи (передает файл с исходной КНФ) и инициирует процесс решения задачи. На основе полученных исходных данных пользовательский агент генерирует множество подзадач и передает их агенту планирования вычислений, который, в свою очередь, формирует задание для каждой подзадачи. Сформированный пул заданий направляется агенту-менеджеру. Агент-менеджер, получив задание, при помощи сервисов мониторинга состояния системы, параметров, заданных пользователем, а также полученных из самого задания, оценивает дальнейшие возможности по его обработке, отправляя запросы другим агентам-менеджерам для проведения тендера. Агенты взаимодействуют на основе координированного сотрудничества, достигаемого в процессе торгов за выполнение задания, которое не смог самостоятельно выполнить получивший его агент. Агент, получивший задание, ставит его в очередь СУПЗ ВК. На этапе выполнения задания запускается решатель hpcsat. Агенты мониторинга отслеживают состояние каждого задания. В случае появления в РВС дополнительных свободных вычислительных ресурсов и пустого пула заданий у агента-менеджера процесс вычислений приостанавливается, одна из активных подзадач снимается с решения, для нее производится дальнейшая декомпозиция, после чего формируются дополнительные задания и процесс вычислений возобновляется. Если решение найдено, задания снимаются с решения или удаляются из очереди (в зависимости от текущего статуса). Если в результате выполнения всех заданий решение не найдено, пользователь получает уведомление о завершении процесса решения с ответом «UNSAT» (функция невыполнима).
Применение HpcSoMas совместно с решателем hpcsat позволяет организовать трехуровневый параллелизм: на уровне РВС (агент-менеджер МАС, rest-сервис), на уровне узла РВС (главный процесс hpcsat, технология MPI, soap-сервис) и на уровне узла кластера (дочерние процессы hpcsat, технология OpenMP). Реализация такого многоуровневого параллелизма показана на рис. 1.
Решатель hpscat. Решатель hpcsat [1, 4] представляет собой MPI-приложение на языке C++. Главный процесс приложения организует динамическую очередь подзадач, получаемых в результате декомпозиции исходной булевой модели. В дочернем процессе может выполняться как многопоточное, так и однопоточное приложение. В качестве такого приложения может использоваться программа, осуществляющая декомпозицию булевой модели методом расщепления либо SAT-решатель (собственный или сторонней разработки). При использовании последовательного решателя в hpcsat реализуется одноуровневый параллелизм по данным, при использовании многопоточного – двухуровневый параллелизм на основе гибридного подхода. Для распараллеливания на уровне узла кластера применяется технология работы с общей памятью.
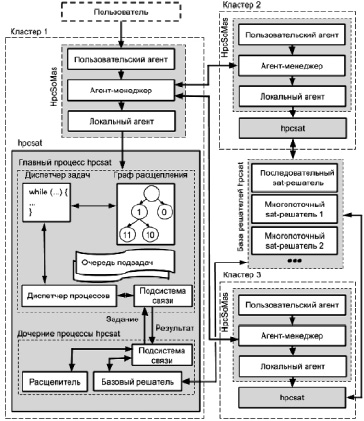
Рис. 1. Схема организации работы МАС HpcSoMas и hpcsat
Для представления узла дерева разработан ряд методов, в том числе рекурсивных, для работы с деревом. Управление состоянием дерева диспетчером подзадач осуществляется с помощью этих методов. Следует отметить, что ветви дерева, для которых в процессе расщепления на этапе упрощения остаточной функции получено значение «UNSAT», отсекаются. Узел дерева становится готовым для формирования подзадачи базовому решателю, когда количество переменных остаточной функции принимает граничные значения, заданные в начале работы hpcsat. Однако в процессе работы может возникнуть ситуация, когда из очереди первыми попадают на выполнение подзадачи, не имеющие решения. Поэтому в разработанном решателе применены механизмы квантования времени и отложенных подзадач. Под квантованием времени понимается прерывание процесса выполнения базового решателя при достижении определенного лимита по времени.
Вычислительные эксперименты. Для проверки работоспособности и эффективности разработанных средств были проведены вычислительные эксперименты [4]. В качестве РВС использована интегрированная кластерная среда, объединяющая вычислительные кластеры суперкомпьютерного центра ИДСТУ СО РАН [9].
Эксперименты проводились на ряде булевых моделей: для классической тестовой задачи о голубях и клетках (оценивались ускорение и эффективность), для четырех задач с соревнований SAT Competition13 [15] (эти задачи не были решены ни одним из участвовавших SAT-решателей за 5000 секунд), для задачи Эйлера о ходе шахматного коня (сформулированной как задача булевой выполнимости).
Результаты тестирования решателя hpcsat при решении задачи о голубях и клетках на вычислительном кластере «Академик В.М. Матросов» [9] (рис. 2, 3) не уступают по эффективности результатам, полученным с помощью ASP-солвера claspar на IBM Blue Gene/P (см. [12], рис. 1). При этом решатель hpcsat достигает более высокой размерности, имея относительное преимущество над claspar по времени решения (табл. 1).
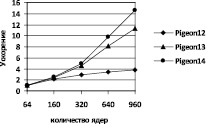
Рис. 2. Ускорение решателя hpcsat на задаче о голубях и клетках
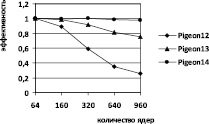
Рис. 3. Эффективность решателя hpcsat на задаче о голубях и клетках
Таблица 1
Время решения (в секундах) задачи о голубях и клетках для размерности 12 и 13
|
hpcsat |
claspar |
|||
|
Число ядер |
640 |
960 |
2048 |
4096 |
|
pigeon12 |
56 |
52 |
111 |
330 |
|
pigeon13 |
368 |
256 |
813 |
573 |
|
pigeon14 |
10434 |
7013 |
– |
– |
Таблица 2
Время решения (в секундах) задач с соревнованиий SAT Competition13
|
КНФ |
Переменных/ дизъюнктов |
HpcSoMas + hpcsat |
|
|
256 ядер |
1024 ядер |
||
|
rbsat-v1150c84314gyes7.cnf |
1150/84314 |
1316 |
514 |
|
toughsat_factoring_inf.cnf |
2878/15516 |
2147 |
553 |
|
gss-25-s100.cnf |
31931/96111 |
1985 |
126 |
|
b04_s_2_unknown_pre.cnf |
123133/801488 |
2988 |
1640 |
Таблица 3
Время решения задачи о ходе шахматного коня различными решателями
|
КНФ |
Количество переменных/дизъюнктов |
Время решения (в секундах) |
|||
|
minisat |
manysat |
penelope |
HpcSoMas+hpcsat |
||
|
knight10 |
10000/1913276 |
– |
– |
7137 |
245 |
|
knight11 |
14641/3456362 |
– |
– |
976 |
554 |
|
knight12 |
20736/5784352 |
– |
– |
– |
1700 |
Результаты, приведенные на рис. 2 и 3, показывают, что с увеличением размерности ускорение приближается к линейному и эффективность становится стабильно высокой.
Для тестирования задач, не решенных в рамках соревнований SAT Competition13, решатель hpcsat успешно получил решение, приведены результаты для 256 и 1024 ядер (табл. 2).
Задача Эйлера о ходе шахматного коня является частным случаем задачи о нахождении гамильтонова пути в графе. Данная задача имеет много решений, но при этом тяжела для SAT-решателей в силу высокой размерности. В табл. 3 приведены результаты решения задачи о ходе шахматного коня, полученные с помощью решателя hpcsat в автономном режиме и в режиме интеграции с МАС HpcSoMas. В табл. 3 для сравнения сведены результаты работы сторонних SAT-решателей (minisat, manysat, penelope) и разработанного решателя hpcsat. Прочерк в графе таблицы присутствует, если решение задачи не было получено (задача заканчивалась аварийно или время ожидания завершения превышало 5 часов).
Приведенные эксперименты позволяют сделать вывод о работоспособности и эффективности разработанных методов и инструментальных средств.
Заключение
В статье рассмотрен сервис-ориентированный подход к организации проблемно-ориентированных распределенных вычислений в РВС. В рамках данного подхода выработана общая концепция реализации многоуровневого параллелизма в РВС, для решения булевых уравнений разработан sat-решатель на основе гибридного метода полного поиска с интеллектуальным возвратом, сочетающий технологии MPI и OpenMP, разработаны мультиагентные средства управления вычислениями, новые высокоуровневые инструментальные средства построения интерфейсов сервис-ориентированных приложений. Предложенный подход позволяет существенно сократить время решения задачи под управлением мультиагентной системы по сравнению со стандартизированными менеджерами ресурсов за счет средств динамической декомпозиции заданий и возможности миграции заданий по узлам вычислительной среды.
Рецензенты:Ружников Г.М., д.т.н., старший научный сотрудник, зав. отделением информационных технологий и систем, Институт динамики систем и теории управления СО РАН имени В.М. Матросова Сибирского отделения Российской академии наук, г. Иркутск;
Данеев А.В., д.т.н., профессор кафедры информационных систем и защиты информации, Иркутский государственный университет путей сообщения, г. Иркутск.
Работа поступила в редакцию 06.03.2015.
Библиографическая ссылка
Богданова В.Г., Горский С.А., Пашинин А.А. СЕРВИС-ОРИЕНТИРОВАННЫЕ ИНСТРУМЕНТАЛЬНЫЕ СРЕДСТВА ДЛЯ РЕШЕНИЯ ЗАДАЧ БУЛЕВОЙ ВЫПОЛНИМОСТИ // Фундаментальные исследования. – 2015. – № 2-6. – С. 1151-1156;URL: https://fundamental-research.ru/ru/article/view?id=36996 (дата обращения: 26.04.2024).



