В последние полтора-два десятка лет в педагогической литературе много говорится о смене классической образовательной парадигмы новой, отвечающей реалиям современного общества, которое оказалось перед проблемой отсутствия достаточного числа кадров, способных сразу после окончания колледжа или вуза компетентно работать в новых условиях. Ситуация, когда специалист с дипломом имеет конечный объем знаний при отсутствии умений его использовать и пополнять, становится сдерживающим фактором развития общества. Этим обусловлено обращение европейского, а вслед за ним и российского образования к компетентностному подходу. Согласно действующим в настоящее время стандартам высшего образования цель обучения – формирование ряда общекультурных и профессиональных компетенций, соответствующих тому или иному направлению подготовки. Компетентностный подход в образовании означает ориентацию на результаты, связанные с усилением практической составляющей обучения, значимой за его пределами, т.е. не на сумме усвоенной обучаемыми информации, а на способности выпускника учебного заведения адаптироваться и самостоятельно действовать в различных ситуациях, решать проблемы различной сложности на основе имеющихся знаний. В этой связи применительно к системе математического образования все большую актуальность приобретает задача привития обучаемым способности применять основные законы естественнонаучных дисциплин в профессиональной деятельности, содержательно интерпретировать реально существующие закономерности с использованием математического аппарата.
В качестве примера иллюстрации возможного применения математического аппарата при интерпретации экономических показателей рассмотрим использование концепции векторной величины. Одной из основных задач экономического анализа является выявление закономерностей в поведении величин экономических показателей и их интерпретация применительно к изучаемым социально-экономическим процессам. Поскольку основная доля экономических показателей является количественными, их обработка, анализ и интерпретация базируются на математических понятиях и алгоритмах.
В математике все величины подразделяются на скалярные (определяемые только своим значением) и векторные (которые, помимо своего значения, характеризуются направлением в некотором математическом (физическом или ином) пространстве). Существуют две формы математического описания векторных величин:
– вектор как направленный отрезок в определенной системе координат (геометрическая форма) – используется преимущественно в физико-технических и геометрических приложениях;
– вектор как кортеж или упорядоченная совокупность чисел (координатная форма) – применяется при построении математических моделей в сфере экономики и управления.
Практически каждый экономист в определенной степени знаком с такими понятиями, как вектор запасов, вектор потребностей, вектор цен и т.п. По указанным выше подходам у специалистов наблюдается консенсус относительно использования и интерпретации векторных величин в сфере экономики. Однако существует проблема, которая на данный момент методологически не проработана, более того, ее наличие замалчивается, поскольку она не соответствует господствующим в настоящее время канонам экономической науки, ориентированным на либеральную модель рыночной экономики. Это – проблема выбора алгоритма интерпретации экономических показателей, получаемых в процессе обработки статистических данных и характеризующих как тенденции развития экономических процессов, так и результаты деятельности отдельных субъектов экономики. Упоминание об этой проблеме есть в работах известного в РФ ученого и публициста С.Г. Кара-Мурзы [1, 2], посвященных формам «перекоса» общественного сознания в последние десятилетия и причинам, их породивших. Предметом настоящей работы является обсуждение возможности и целесообразности использования «концепции векторной величины» применительно к интерпретации экономических показателей, величины которых получены в процессе сбора и обработки статистических данных о процессах, протекающих в сфере экономики. Суть проблемы в следующем. Как правило, абсолютное большинство экономических показателей, публикуемых в научных работах, статистических справочниках и в СМИ описываются одним числом, т.е. с точки зрения математики являются скалярными величинами. Однако последующая их интерпретация может осуществляться по-разному, а именно либо на основе концепции скалярной величины, либо на основе концепции векторной величины.
Самым простым с точки зрения технической реализации и распространенным с позиции общепринятой методологии анализа является алгоритм интерпретации скалярных величин, основанный на сравнении абсолютных значений показателей. Так, если за отчетный период темп прироста уровня дохода у фирмы А составил 10 %, а у фирмы В – 35 %, то сопоставление этих показателей как скалярных величин позволяет сделать однозначный вывод – деятельность фирмы В была эффективнее, чем фирмы А. К сожалению, этот подход имеет существенный недостаток: значительная часть полезной информации (нередко – наиболее ценной) при этом теряется, что может привести к неадекватной интерпретации изучаемых социально-экономических ситуаций и принятию ошибочных управленческих решений. Кроме того, упрощенный алгоритм интерпретации поведения экономического показателя как скалярной величины позволяет скрывать от общественного внимания ряд истинных факторов, формирующих величину анализируемого показателя. Такая возможность является весьма эффективным инструментом манипуляции сознанием людей и позволяет заинтересованным лицам трактовать происходящие в обществе процессы в выгодном для себя свете.
При изложении сути интерпретации показателей на основе концепции векторной величины воспользуемся методом аналогии, обращаясь к понятиям, используемым в векторной алгебре. Это позволит нам ввести на интуитивно-образном уровне такие необходимые для дальнейшего обсуждения понятия, как абстрактное социально-экономическое пространство и система координат в этом пространстве, экономический показатель как вектор в выбранном пространстве. Отметим, что под социально-экономическим пространством в работе предлагается понимать некоторое абстрактное понятие, в основных своих чертах аналогичное математическому пространству, а векторный экономический показатель будем трактовать как величину, которая характеризуется своим численным значением и определенной социально-экономической направленностью.
Предлагаемый подход к интерпретации экономических показателей как векторных величин основан на тезисе: в математике непосредственное сравнение по абсолютной величине допустимо только для коллинеарных (однонаправленных) векторов. Для векторов, ориентированных в различных направлениях рассматриваемого математического пространства, корректным является только сопоставление соответствующих проекций этих векторов на оси выбранной системы координат. Согласно методу аналогии имеем следующий тезис: непосредственное сравнение величин экономических показателей, формирование которых происходило за счет процессов, имеющих существенно различную социально-экономическую направленность (различный вектор предпочтений (целеполагания) в социально-экономическом пространстве), представляется методологически некорректной процедурой (формы проявления такой некорректности будут рассмотрены в приведенных ниже примерах). Сущность интерпретации экономического показателя как векторной величины заключается в следующем:
– значение экономического показателя, представленного одним числом, рассматривают как своеобразный аналог абсолютного значения векторной величины в математике;
– в рамках контекстного анализа исследуемого социально-экономического явления или процесса вводят понятие (модель) абстрактного социально-экономического пространства определенной размерности (по аналогии с абстрактным математическим пространством Rn) и определяют в нем систему координат, описывающую ключевые социально-экономические направления деятельности, в рамках которых осуществлялось формирование наблюдаемой величины экономического показателя;
– используя дополнительную информацию о процессах, формирующих величину экономического показателя, оценивают вклад факторов, выбранных в качестве системы координат абстрактного социально-экономического пространства, что по аналогии соответствует определению величин проекции математического вектора на оси координат;
– сопоставляя величины одноименных проекций для двух или более сравниваемых между собой экономических показателей, получают дополнительную информацию о механизме процессов формирования каждой из наблюдаемых величин экономических показателей, подвергнутых процедуре интерпретации.
Рассмотрим смысл использования концепции векторной величины при интерпретации экономических показателей на условных примерах, помогающих проиллюстрировать обучаемым суть поставленной проблемы.
Пример 1. В экономическом анализе при изучении динамики экономических показателей используется темп прироста Тпр,
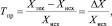 (*)
(*)
определяемый как безразмерная величина или измеряемый в процентах, где Xтек – текущее значение; Xисх – исходное значение (базис); ΔX = Xтек – Xисх – абсолютное приращение экономического показателя. Если по данным статистики темп прироста объема производства определенного вида продукции за некоторый период в фирме А составил 30 %, а в фирме В – 10 %, то интерпретация на основе концепции скалярной величины приводит к однозначному выводу: деятельность фирмы А была эффективнее (в три раза), чем фирмы В. Но на самом деле не все так просто. Как говорили мудрые люди – «Дьявол кроется в деталях». Рассмотрим некоторые из такого рода «деталей». Из формулы (*) следует, что при сопоставимых величинах абсолютного приращения ΔХ величина Тпр существенно зависит от исходного значения Xисх. Если выяснится, что исходное значение объема производства фирмы В в 20 раз больше, чем у фирмы А, то вывод о приоритете деятельности фирмы А перестает быть столь очевидным, поскольку абсолютный прирост объема производства фирмы В (в сопоставимых натуральных показателях) оказывается в 6,67 раз выше, чем у фирмы А. Здесь мы сталкиваемся с проблемой адекватности процедуры интерпретации реальным условиям, вызванной влиянием «масштабного эффекта»: попытки сравнивать относительные показатели для разномасштабных субъектов экономики могут приводить к неадекватным выводам и ошибочным управленческим решениям. Чтобы избежать такого рода ошибок, рассмотрим темп прироста Тпр как вектор в двумерной системе координат (Хисх; ΔХ), тогда для наглядности Тпр для фирм А и В можно представить как векторы в декартовой системе координат на плоскости (рис. 1).
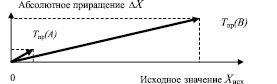
Рис. 1. Темпы прироста фирм А и В как векторы в декартовом пространстве
Из рис. 1 видно: эти векторы являются разнонаправленными и непосредственное сопоставление величин Тпр(А) и Тпр(В) является некорректным. Другой «деталью» могут быть доли социально ориентированной и рыночно ориентированной продукции в общем объеме производства фирм А и В. Как правило, производство социально ориентированной продукции является менее прибыльным для фирмы, но позволяет государству решать социальные проблемы и обеспечивать должный уровень национальной безопасности. Необходимость расстановки важных для национальной безопасности приоритетов требует более глубокого анализа экономической информации, одним из инструментов которого может служить интерпретация экономических показателей на основе концепции векторной величины.
Пример 2. Пусть в ходе анализа статистических данных было установлено, что за отчетный период темп прироста стоимости потребительской корзины (ПК) составил а = 10 %. Хорошо это или плохо? Алгоритм интерпретации показателя а как скалярной величины ответа на данный вопрос не дает, фиксируется сам факт роста стоимости ПК без последующего его содержательного анализа. Попытаемся интерпретировать величину а с использованием концепции векторной величины. Рост стоимости ПК возможен по двум основным причинам: за счет роста цен (инфляция) или за счет расширения ассортимента товаров и услуг, входящих в состав ПК. Для анализа введем двумерную систему координат в модели абстрактного социально-экономического пространства: одна координата будет определять влияние инфляции (роста цен на товары и услуги), а другая – состав потребительской корзины. Математическим аналогом такой модели может быть декартова система координат на плоскости. На основе дополнительного анализа исходных статистических данных, использованных для расчета величины а, оценим вклад каждого из факторов (инфляция, изменение состава ПК) в наблюдаемую величину а, т.е. найдем координату а*, определяемую инфляцией, и координату а**, определяемую изменением структуры ПК. В данном случае темп прироста а можно представить в виде вектора (а*; а**) в координатной форме, который содержит дополнительную информацию для адекватной интерпретации величины а:
– если рост стоимости ПК был обусловлен инфляцией (а* >> а** ), то это – «плохой» результат, поскольку произошло ухудшение социального положения населения;
– если же рост стоимости ПК был обусловлен расширением состава ПК (а* << а**), то это – «хороший» результат, способствующий улучшению социально-экономического положения населения.
Пример 3. На основе статистических данных установлено, что в отчетном периоде темп прироста дохода от кредитных операций для банка А составил a = 30 %, а у банка В – b = 10 %. Требуется дать интерпретацию полученным результатам, т.е. оценить эффективность работы этих банков. Если рассматривать темп прироста как скалярную величину, то из условия 30 > 10 % следует однозначный вывод о том, что деятельность А как субъекта рыночной экономики была эффективнее, чем В. Никакой иной информации о деятельности А и В из этих результатов получить нельзя. Если же требуется оценить работу А и В с учетом возможных социально-экономических последствий их деятельности, то темпы прироста a и b следует уже рассматривать как векторные величины в некоторой системе координат, отражающей не только чисто экономический, но и социальные эффекты от их деятельности (средний уровень процента за кредит, средний срок кредитования). Пусть в ходе анализа выяснилось, что банк В специализировался на долгосрочном кредитовании малого и среднего бизнеса в сфере сельского хозяйства и промышленности под сравнительно низкий процент, что неизбежно привело к сравнительно невысоким его доходам. В свою очередь, банк А занимался краткосрочным кредитованием коммерческих операций под высокий процент и тем самым обеспечил себе высокий уровень доходности. С точки зрения основного постулата либеральной рыночной экономики «Основная цель деятельности – получение максимального дохода» поведение банка А абсолютно адекватно и его деятельность следует признать более эффективной. С точки зрения перспектив развития социально-экономических процессов банк А действовал, создавая в угоду своей сиюминутной выгоде предпосылки для предстоящих финансовых кризисов, и с этих позиций деятельность банка А следует рассматривать как деструктивную, а деятельность В – как социально ориентированную и созидательную.
В качестве простой, но полезной для практики модели экономического пространства можно использовать двумерное абстрактное пространство с координатами «рыночно-ориентированная деятельность» и «социально-ориентированная деятельность». Для наглядности здесь можно воспользоваться декартовой системой координат (рис. 2).

Рис. 2. Ориентация вектора целеполагания деятельности субъектов экономики (А – преимущественно рыночно-ориентированная деятельность, В – преимущественно социально-ориентированная деятельность)
Разделяя величину анализируемого экономического показателя |а| на два слагаемых а* и а** (см. пример 2), мы представляем скаляр а в форме вектора (а*; а**), где а* + а** = |а|, и определяем ориентацию вектора целеполагания деятельности субъекта экономического процесса. Значение любого экономического показателя, выраженного в форме числа, всегда включено в определенный контекст, который позволяет наполнить это число смыслом.
Приводимые в экономической литературе значения различных экономических показателей нередко приобретают ложный смысл из-за того, что они не помещены в соответствующую реальной ситуации систему координат и их адекватная интерпретация становится невозможной. Этот механизм нередко осознанно используется в целях манипуляции сознанием людей, неспособных или не желающих вникать в скрытую сущность представленной экономической информации. Из приведенных выше примеров видно, как изменение методологии интерпретации одних и тех же величин экономического показателя может привести к противоположным выводам. Использование «концепции векторной величины» при интерпретации экономических показателей расширяет ассортимент допустимых к использованию критериев оптимальности и позволяет осуществлять более глубокий анализ изучаемого явления до того, как будет принято то или иное управленческое решение.
Рецензенты:
Чекулина Т.А., д.э.н., профессор, декан факультета бизнеса и рекламы, ФГБОУ ВПО «Орловский государственный институт экономики и торговли», г. Орел;
Малявкина Л.И., д.э.н., заведующая кафедрой математики, информатики и информационных технологий, ФБОУ ВПО «Орловский государственный институт экономики и торговли», г. Орел.
Библиографическая ссылка
Савина А.Г., Блок А.В. ИНТЕРПРЕТАЦИЯ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ С ИСПОЛЬЗОВАНИЕМ КОНЦЕПЦИИ ВЕКТОРНОЙ ВЕЛИЧИНЫ В РАМКАХ РЕАЛИЗАЦИИ КОМПЕТЕНТНОСТНОГО ПОДХОДА К ОБУЧЕНИЮ // Фундаментальные исследования. – 2015. – № 2-21. – С. 4775-4779;URL: https://fundamental-research.ru/ru/article/view?id=38068 (дата обращения: 08.05.2024).



