Одной из наиболее сложных и до конца не решенных задач в теории образования новой фазы является процесс образования начальных ядер конденсации. Эти ядра могут иметь небольшой размер и состоять всего из нескольких молекул, называемых кластерами тел, жидкостей и газов и называемая микрокластером. Микрокластеры представляют собой мельчайшие агрегаты, включающие от двух до нескольких сотен и более атомов. Современные квантово-химические методы позволяют найти моменты инерции, частоты внутримолекулярных и межмолекулярных колебаний в кластерах, а также энергию их диссоциации. На основании этих расчетов оказывается возможным найти все термодинамические, а также кинетические характеристики кластеров. В термодинамику компонент природного газа, в том числе воды и паров воды, положен кластерный подход.
Вычисление скорости зародышеобразования кластеров воды по классической теории
Классическая теория зародышеобразования создана еще в 30-е годы и опирается на два основных приближения: модель Сцилларда и жидкокапельную модель. В модели Сцилларда предполагается, что перенасыщенный пар состоит из смеси пара мономеров и кластеров, содержащих различное число молекул. Кластеры могут расти, и испарятся, присоединяя при этом или теряя только одну молекулу. В рамках этой модели можно получить для скорости стационарного изометрического зародышеобразования компактное выражение
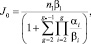 (1)
(1)
где n1 – концентрация мономеров (предполагается, что пар мономеров не истощается в процессе конденсации); βi – скорость присоединения молекулы к кластеру; αi – скорость испарения; g* – критический размер зародыша. Используя далее капельную модель, т.е. предполагая, что кластеры сферические и однородные, получим для скорости нуклеации выражение
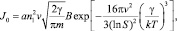
где a – коэффициент прилипания; v – объем одной молекулы жидкости; γ – поверхностное натяжение; 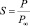 – пересыщение; B – поправка Варнарда, которая возникает при последовательном кинетическом подходе и которая отсутствует при расчете из классических термодинамических соображений, т.е. при вычислении работы, необходимой для создания зародыша размера g. Поверхностное натяжение для кластеров воды малых размеров было вычислено с большой точностью в работе [1] (рис. 1). Данные результаты были сделаны по расчету размера кластера по точным координатам атомов в кластере. Отсюда видно, что реальное поверхностное натяжение кластеров малых размеров на 30–50 % меньше, чем для обычных капель жидкости. g* – в этом случае для рассматриваемых температур T = 230–250 K получается порядка 3, в то время как по классической теории g* ~ 5, для данных температур.
– пересыщение; B – поправка Варнарда, которая возникает при последовательном кинетическом подходе и которая отсутствует при расчете из классических термодинамических соображений, т.е. при вычислении работы, необходимой для создания зародыша размера g. Поверхностное натяжение для кластеров воды малых размеров было вычислено с большой точностью в работе [1] (рис. 1). Данные результаты были сделаны по расчету размера кластера по точным координатам атомов в кластере. Отсюда видно, что реальное поверхностное натяжение кластеров малых размеров на 30–50 % меньше, чем для обычных капель жидкости. g* – в этом случае для рассматриваемых температур T = 230–250 K получается порядка 3, в то время как по классической теории g* ~ 5, для данных температур.
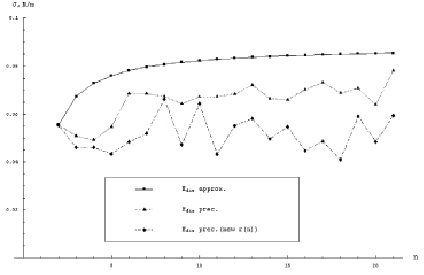
Рис. 1. Зависимость поверхностного натяжения от размера кластера
Выражение (1) переходит в
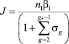 ,
,
где
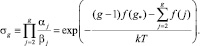
Для функции f(g) была взята зависимость, полученная методом молекулярной динамики в эксперименте [6]. В классической теории нуклеации скорость испарения кластера, содержащего g молекул,
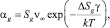
где 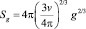 – площадь поверхности кластера, состоящего из g – молекул; v – объем одной молекулы (мономера), и тогда
– площадь поверхности кластера, состоящего из g – молекул; v – объем одной молекулы (мономера), и тогда
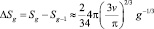 – изменение поверхности за счет испарения одной молекулы.
– изменение поверхности за счет испарения одной молекулы.
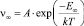 – скорость испарения с единицы площади плоской границы раздела; E∞ – теплота испарения с плоскости.
– скорость испарения с единицы площади плоской границы раздела; E∞ – теплота испарения с плоскости.
В классической теории нуклеации скорость роста зародышей βg выражают через число столкновений с мономерами в единицу времени:
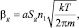
где a – коэффициент прилипания, величина неопределенная и может лежать от 0,01 до 1.
На основе вышеприведенных данных была вычислена скорость зародышеобразования для жидкокапельной модели с поправкой Варнарда (2) (рис. 2). Полученные данные были сравнены с последними экспериментальными данными работы [5]. Как видно, классический подход к теории зародышеобразования не дает удовлетворительных результатов. Далее будет использован и продемонстрирован квантово-механический подход для расчета скорости зародышеобразования.
Вычисление скорости зародышеобразования кластеров воды по квантово-механической теории
Рассмотрим систему, состоящую из газофазных молекул А1 конденсирующегося вещества (мономеров) и молекулярных агрегатов An (кластеров), состоящих из двух и более молекул: n ≥ 2. Кластер An размерности n обладает энергией диссоциации (разрыва связи) En, тремя моментами инерции IA(n), IB(n), IC(n), а также 3nl – 6 колебательными степенями свободы, из которых (3l – 6)n относятся к внутримолекулярным, а (6n – 6) – к межмолекулярным колебаниям (l – число атомов в мономере).
Рассмотрим сначала упрощенную модель кластеризации, предполагая, что рост кластеров происходит за счет присоединения к ним одиночного мономера молекулы-ассоциации, а их разрушение происходит через промежуточную стадию – образование и распад активированного комплекса [2]. Опуская стадию активированного комплекса, учитывая только конечный продукт реакции, цепочка элементарных процессов образования и гибели кластеров An может быть записана в суммарном виде:
Ka(n), An + A1 + M ó An + 1 + M, Kd(n + 1). (2)
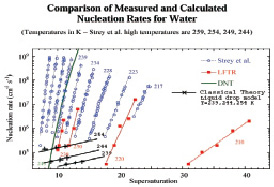
Рис. 2. Скорость зародышеобразования по классической теории (жидкокапельная модель)
Здесь M – любая молекула или кластер газовой фазы; Ka(n) и Kd(n + 1) – константы скоростей прямых и обратных реакций; Ka(n) – константа скорости присоединения мономера к кластеру An, а Kd(n + 1) – константа скорости диссоциации кластера An + 1 на кластер An и мономер.
Для концентрации Nn кластеров вида An на основе (2) можно записать уравнение изменения их со временем в виде [2]:
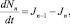 (3)
(3)
где 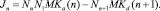
Здесь Jn – поток кластеров в пространстве числа мономеров в них, т.е. число кластеров, переходящих в единицу времени из точки n в точку n + 1.
В условиях термодинамического равновесия скорость прямых и обратных реакций Ka(n), Kd(n + 1) связаны через константу равновесия:
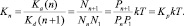
Здесь Pi = aiP, 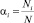 – парциальное давление и мольная доля компонента i;
– парциальное давление и мольная доля компонента i; 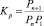 – константа равновесия реакции (2), выраженная в терминах парциального давления компонентов ([Kp] = атм–1). Расчет константы скорости диссоциации кластера основан на теории мономолекулярных реакций РРКМ [4], здесь приведен только окончательный результат:
– константа равновесия реакции (2), выраженная в терминах парциального давления компонентов ([Kp] = атм–1). Расчет константы скорости диссоциации кластера основан на теории мономолекулярных реакций РРКМ [4], здесь приведен только окончательный результат:
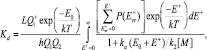
где E* = E+ + E0;
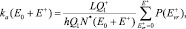
здесь L – число путей, эквивалентных в смысле энергетики (например, L = 2 для диссоциации H2O на H и OH); Q1 и 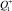 – статистические суммы для вращений в молекуле и активированном комплексе соответственно (в расчетах принималось
– статистические суммы для вращений в молекуле и активированном комплексе соответственно (в расчетах принималось 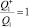 ); Q2 – полная (колебательная и вращательная) статистическая сумма для диссоциирующей молекулы;
); Q2 – полная (колебательная и вращательная) статистическая сумма для диссоциирующей молекулы; 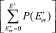 – количество колебательно-вращательных состояний активированного комплекса в интервале энергий [0, Е+]; N* – плотность колебательно-вращательных уровней реагента. Число состояний активизированных комплексов и плотность энергии молекул реагента малых размеров подсчитывались путем прямого пересчета (для этого все частоты нормальных колебаний были разбиты на 9 групп). Для больших кластеров использовалось аналитическое приближение Виттена – Рабиновича [4]. Константа образования кластера Ка(n) определялась через константу диссоциации Кd(n + 1) и константу равновесия Kn.. В квазиравновесных условиях dNn/dt = 0, следовательно, J не зависит от n, так как согласно (3)
– количество колебательно-вращательных состояний активированного комплекса в интервале энергий [0, Е+]; N* – плотность колебательно-вращательных уровней реагента. Число состояний активизированных комплексов и плотность энергии молекул реагента малых размеров подсчитывались путем прямого пересчета (для этого все частоты нормальных колебаний были разбиты на 9 групп). Для больших кластеров использовалось аналитическое приближение Виттена – Рабиновича [4]. Константа образования кластера Ка(n) определялась через константу диссоциации Кd(n + 1) и константу равновесия Kn.. В квазиравновесных условиях dNn/dt = 0, следовательно, J не зависит от n, так как согласно (3) 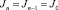 для любого n. В этом случае
для любого n. В этом случае
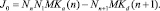
В равновесных условиях, когда скорости любых прямых и обратных процессов уравновешиваются
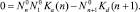
Здесь 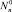 – квазиравновесная функция распределения в отсутствии потока (J0 = 0) и решение
– квазиравновесная функция распределения в отсутствии потока (J0 = 0) и решение 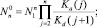
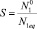 – пересыщение. Здесь
– пересыщение. Здесь 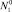 – числовая плотность мономеров; N1eq – равновесная числовая плотность мономеров над кластерами предельно большого размера.
– числовая плотность мономеров; N1eq – равновесная числовая плотность мономеров над кластерами предельно большого размера.
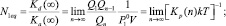
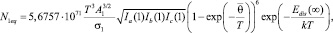
где Edis(∞) – энергия отрыва мономера от кластера бесконечно большого размера, «среднестатистическая» характеристическая колебательная температура кластера размера n – 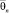 определяется из следующего соотношения:
определяется из следующего соотношения:
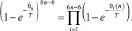
Квазиравновесное распределение принимает вид
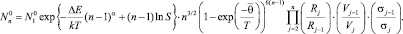
Здесь 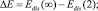 Edis(∞) – энергия отрыва мономера от кластера бесконечно большого размера; Edis(2) – энергия диссоциации димера; α ∈ (0, 1) – параметр [2]. В работе [2] было получено выражение для квазиравновесного распределения кластеров, содержащих n мономеров вида
Edis(∞) – энергия отрыва мономера от кластера бесконечно большого размера; Edis(2) – энергия диссоциации димера; α ∈ (0, 1) – параметр [2]. В работе [2] было получено выражение для квазиравновесного распределения кластеров, содержащих n мономеров вида
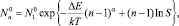
полностью совпадающее с выражением, полученным в приближении жидко-капельной модели классической теории конденсации, если
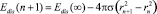
и α = 2/3, где rn, σ – радиус и поверхностное натяжение.
Выражение (2) отличается от классического и выражения работы [2] явным учетом структуры и энергетических характеристик межмолекулярных квантовых движений в кластере размерности n.
Статистическая сумма идеального газа с внутренними степенями свободы, состоящего из N неразличимых идентичных частиц – кластеров размерности n, равна [3]:
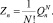
Таким образом, для одного моля кластеров размерности n
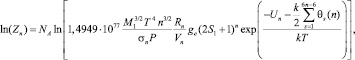 (4)
(4)
где NA – число Авогадро; M1 – масса мономера; ge – вырождение электронного уровня кластера; S1 – ядерный спин мономера.
Знание Zn позволяет вычислить все необходимые термодинамические функции для одного моля кластеров размерности n [3]. В квазиравновесном приближении приращение свободной энергии Гиббса может быть приведено к виду
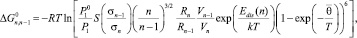
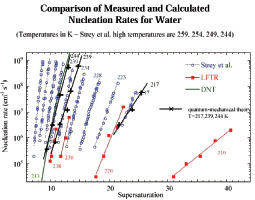
Рис. 3. Скорость зародышеобразования по квантово-механической теории для различных T (217, 239, 244, K)
Решение неоднородной системы в квазистационарном приближении ищется в виде [7]:
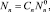
где 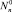 – квазиравновесное распределение кластеров по размерам при (J0 = 0).
– квазиравновесное распределение кластеров по размерам при (J0 = 0).
Решение неоднородной системы в случае (J0 ≠ 0) имеет вид
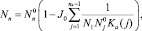
где 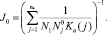
При известных константах ассоциации и диссоциации кластеров находится квазиравновесное решение 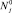 и вычисляется число зародышей в единице объема, переходящих в единицу времени из точки n (кластера размерности n) в точку n + 1 (кластера размерности n + 1) для системы с плотностью мономеров N1.
и вычисляется число зародышей в единице объема, переходящих в единицу времени из точки n (кластера размерности n) в точку n + 1 (кластера размерности n + 1) для системы с плотностью мономеров N1.
Числовая плотность кластеров в стационарном состоянии меньше соответствующей числовой плотности в квазиравновесном состоянии. Уменьшение числовой плотности кластеров в стационарном состоянии по сравнению с квазиравновесным тем больше, чем больше его размер n.
Для подсчета J0 была использована компьютерная программа работы [1]. Как видно из рис. 3, при использовании данного квантово-механического подхода получается результат близкий к экспериментальному, что подтверждает необходимость использования данного подхода. Далее будет продемонстрирован квантово-механический подход для вычисления термодинамических функций кластеров воды.
Выводы
Было произведено сравнение двух теорий для нахождения скорости зародышеобразования воды – классической и квантово-механической. Основная проблема в определении скорости зародышеобразования в классической теории конденсации, как было выявлено в работах многих авторов, сводится к тому, что необходимо с большой точностью описывать поверхностное натяжение g, которое вносит большой вклад в саму скорость. Классическая жидкокапельная модель не может дать точной величины g для малых частиц, вследствие чего возникает расхождение с экспериментом. То есть для малых кластеров понятие g теряет смысл. Были проведены расчеты энергий и теплоемкостей различных кластеров при различных температурах и давлениях, их вклад в общую теплоемкость системы.
В итоге получается, что для корректного описания термодинамических функций вещества, в частности воды и ее паров, необходимо учитывать вклад кластеров в общие свойства системы. В частности, ярко выражено отличие теплоемкости мономера воды и теплоемкости воды с учетом вклада димеров, тримеров и тетрамеров. Для исследования свойств кластеров и их влияния на окружающую среду необходимо привлечение квантово-механических представлений. Кроме того, развитие теории кластеров поможет лучше освоить технологию добычи клатратов метана – потенциального источника энергии в будущем.
Работа выполнена при поддержке РФФИ (Грант № 14-07-00564-а).
Рецензенты:
Николаев В.С., д.т.н., профессор, кафедра математики, Московский физико-технический институт (государственный университет), г. Жуковский;
Чернышев С.Л., д.ф.-м.н., профессор, ФГУП «Центральный аэрогидродинамический институт им. профессора Жуковского», г. Жуковский.
Библиографическая ссылка
Хлопков А.Ю. КОНДЕНСАЦИЯ ПАРОВ ВОДЫ. КЛАССИЧЕСКИЙ И КВАНТОВЫЙ ПОДХОДЫ // Фундаментальные исследования. – 2015. – № 7-4. – С. 782-787;URL: https://fundamental-research.ru/ru/article/view?id=38821 (дата обращения: 26.04.2024).



