1
Брюханова Т.Н.
1
Иванова Г.Д.
2
Кузин А.А.
2
Рекунова Н.Н.
2
1 ФГБОУ ВПО «Тихоокеанский государственный университет»
2 ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения»
Светоиндуцированная модуляция рельефа используется для записи оптической информации, для создания термооптических управляемых дефлекторов. В данной работе теоретически исследовано термозеркало на основе тонкой полимерной пленки. При облучении пучком излучения c синусоидальным пространственным распределением интенсивности нагрев пленки приводит к образованию соответствующего рельефа на ее поверхности. Предложена модель явления, в которой светоиндуцированное расширение тонкой пленки приводит к соответствующей ее деформации. На основе решения двумерной нестационарной тепловой задачи проанализированы пространственно-временные характеристики коэффициента рельефной нелинейности, обусловленной тепловым расширением среды. Тепловая задача решается в предположении, что теплоотвод от поверхности пленки конвективный и теплопередача вдоль пленки пренебрежимо мала. Предложено использовать термозеркало для компенсации тепловой линзы в тонкослойных жидкофазных нелинейно-оптических элементах.
динамическая голография
рельефные голограммы
тепловое расширение среды
обращение волнового фронта
1. Бетин А.А. Отражение излучения СО2-лазера при вырожденном четырёхволновом взаимодействии в жидкостях / А.А. Бетин, Е.А. Жуков, О.В. Митропольский // Квантовая электроника. – 1985. – т. 12. – № 9. – C. 1890.
2. Голубцов А.А. Обращение волнового фронта при светоиндуцированном профилировании формы поверхности поглощающего вещества / А.А. Голубцов, Н.Ф. Пилипецкий, А.Н.Сударкин, В.В. Шкунов // Квантовая электроника. – 1981. – Т. 8.
3. Иванов В.И. Влияние термодиффузии на термолинзовый отклик в жидкофазной дисперсной среде / В.И. Иванов, Г.Д. Иванова, В.К. Хе // Физико-химические аспекты изучения кластеров, наноструктур и наноматериалов, межвуз. сб. науч. тр. / под общ. ред. В.М. Самсонова, Н.Ю. Сдобнякова. – Тверь: Твер. гос. ун-т, 2013. – Вып. 5. – С. 112–115.
4. Иванов В.И. Термоиндуцированные механизмы записи динамических голограмм^ монография. – Владивосток: Дальнаука, 2006. – 143 с.
5. Иванов В.И., Иванова Г.Д., Хе В.К. Тепловое самовоздействие излучения в тонкослойной жидкофазной среде // Современные проблемы науки и образования. – 2014. – № 6. URL: www.science-education.ru/120-17046.
6. Иванов В.И., Илларионов А.И., Коростелева И.А. Обращение волнового фронта непрерывного излучения в условиях сильного самовоздействия // Письма в «Журнал технической физики». – 1997. – Т. 23. – № 15. – С. 60–63.
7. Иванов В.И., Карпец Ю.М., Окишев К.Н., Ливашвили А.И. Термодиффузионный механизм просветления двухкомпонентной среды лазерным излучением // Известия Томского политехнического университета. – 2007. – Т. 311. – № 2. – С. 39–42.
8. Иванов В.И., Кузин А.А., Ливашвили А.И., Хе В.К. Динамика светоиндуцированной тепловой линзы в жидкофазной двухкомпонентной среде // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Физико-математические науки. – 2011. – Т. 4. – № 134. – С. 44–46.
9. Иванов В.И., Ливашвили А. И., Брюханова Т. Н., Рекунова Н. Н. Пространственно-временные характеристики термоиндуцированного механизма записи рельефных динамических голограмм // Вестник Тихоокеанского государственного университета. – 2011. – № 1. – С. 065–068.
10. Иванов В.И., Ливашвили А.И. Электрострикционный механизм самовоздействия излучения в жидкости с наночастицами // Вестник Новосибирского государственного университета. Серия: Физика. – 2009. – Т. 4. – № 2. – С. 58–60.
11. Иванов В.И., Ливашвили А.И. Эффект Дюфура в дисперсной жидкофазной среде в поле гауссова пучка // Физико-химические аспекты изучения кластеров, наноструктур и наноматериалов, межвуз. сб. науч. тр. / под общ. ред. В.М. Самсонова, Н.Ю. Сдобнякова. – Тверь: Твер. гос. ун-т, 2013. – Вып.5. – С. 116–119.
12. Иванов В.И., Ливашвили А.И., Окишев К.Н. Термодиффузионный механизм изменения оптического пропускания двухкомпонентной среды // Известия высших учебных заведений. Приборостроение. – 2008. – Т. 51. – № 3. – С. 50–53.
13. Ливашвили А.И., Иванова Г.Д., Хе В.К. Стационарный термолинзовый отклик наножидкости// Физико-химические аспекты изучения кластеров, наноструктур и наноматериалов, межвуз. сб. науч. тр. / под общ. ред. В.М. Самсонова, Н.Ю. Сдобнякова. – Тверь: Твер. гос. ун-т, 2014. – Вып. 6. – С. 227–230.
14. Окишев К.Н. Термодиффузионный механизм нелинейного поглощения суспензии наночастиц / К.Н. Окишев, В.И. Иванов, С.В. Климентьев, А.А Кузин, А.И. Ливашвили // Оптика атмосферы и океана. – 2010. – Т. 23. – № 2. – С. 106–107.
15. Ivanov V.I., Illarionov A.I., Korosteleva I.A. Technical Physics Letters. – 1997. – Vol. 23. – № 1. – Р. 600–601.
Различные механизмы оптической нелинейности на поверхности раздела сред широко используются в динамической голографии для хранения и обработки оптической информации [1–4, 9]. При этом динамическая голограмма представляет собой решетку амплитудного френелевского коэффициента отражения r («поверхностную» голограмму). Соответствующий метод обращения волнового фронта излучения отражающей поверхностью (ОВФ-П) впервые предложен Б.Я. Зельдовичем с сотрудниками [2]. Особенность этого метода состоит в том, что здесь требуется только одна опорная волна Е0, которая записывает решетку δr, интерферируя с сигнальной волной Е3 (δr ~ Е0Е3), и одновременно дифрагирует на этой отражательной решетке. Фазовое сопряжение будет точным, если волновой фронт опорной волны совпадает с формой отражающей поверхности (которая может быть и неплоской).
В одной из первых экспериментальных работ по записи поверхностных динамических голограмм было использовано тепловое расширение среды [1]. Там же проведен анализ нелинейности для стационарного режима записи, а частотно-временные и пространственные характеристики нелинейности не исследованы.
Целью данной работы является исследование пространственно-временной зависимости коэффициента рельефной нелинейности, обусловленной тепловым расширением слоя среды.
Независимо от природы «поверхностной» нелинейности, ее можно описать, используя зависимость комплексного амплитудного коэффициента отражения от интенсивности 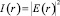 (в обозначениях работы [2]) падающего излучения:
(в обозначениях работы [2]) падающего излучения:
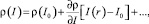 (1)
(1)
где r – радиус-вектор в плоскости раздела сред; I0 – среднее значение интенсивности излучения; 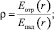
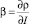 – коэффициент поверхностной нелинейности.
– коэффициент поверхностной нелинейности.
Пусть на зеркально отражающую поверхность падает строго нормально плоская волна E0exp(–ikz), под углом θ3 к нормали когерентная с ней слабая сигнальная волна E3 (рис. 1). В результате интерференции волн E0 и E3 коэффициент отражения становится промодулированным [2]:
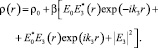 (2)
(2)
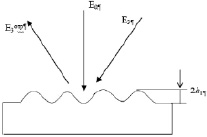
Cхема записи рельефной голограммы
Поглощение света с поперечно-неоднородным профилем интенсивности I(r) вызывает неоднородный прогрев поверхностных слоев материала зеркала. Из-за теплового расширения в максимуме интенсивности зеркало выпучивается навстречу пучку, т.е. образуется решетка рельефа [2]:
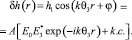 (3)
(3)
Для нахождения амплитуды рельефа сначала необходимо решить следующую двумерную нестационарную тепловую задачу:
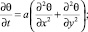 (4)
(4)
θ(x, y, t) = T(x, y, t) – T0, (5)
где T0 – начальная температура среды.
С граничными и начальными условиями
0 ≤ x < ℓ; –∞ < y < ∞; θ(x, y, 0) = 0; (6)
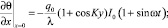
θ(x, y, ℓ) = 0, (7)
где K = kθ3 – волновой вектор интерференционной решетки; 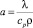 – температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
– температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
Удобно вести функцию V(x), удовлетворяющую уравнению
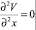 (8)
(8)
и условиям:
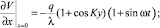
V(ℓ) = 0. (9)
Из равенств (8) и (9) можно найти вид функции V(x):
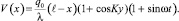 (10)
(10)
Решение исходной задачи ищем в виде
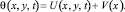 (11)
(11)
Подстановка (11) в (5) приводит к задаче вида
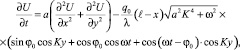 (12)
(12)
где 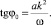
Соответствующие начальные и граничные условия будут иметь вид
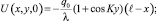
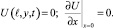 (13)
(13)
Используя функцию Грина [5] для задачи (12)–(13) и проводя соответствующие интегрирования, получим искомое выражение для температуры:
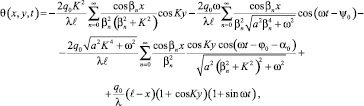
где 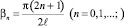
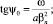
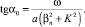
Модуляция рельефа определяется тепловым расширением среды:
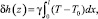 (14)
(14)
где γ – коэффициент линейного теплового расширения среды.
Учитывая, что 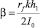 [2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
[2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
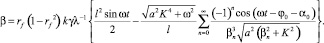 (15)
(15)
Полученное выражение показывает, как коэффициент рельефной нелинейности зависит от частоты модуляции падающего излучения и волнового вектора динамической голограммы. Проведенный анализ может представлять интерес для расчета пространственно-временных характеристик фазосопряженных зеркал, используемых в прикладных задачах нелинейной оптики [1–8], для компенсации термонаведенных искажений в нелинейных средах [10–15].
Рецензенты:
Карпец Ю.М., д.ф.-м.н., профессор кафедры «Физика и теоретическая механика», ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск;
Криштоп В.В., д.ф.-м.н., профессор кафедры физики, проректор по учебной работе, ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск.
Библиографическая ссылка
Брюханова Т.Н., Иванова Г.Д., Кузин А.А., Рекунова Н.Н. ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ТЕРМООПТИЧЕСКОЙ РЕЛЬЕФОГРАФИИ // Фундаментальные исследования. – 2015. – № 8-2.
– С. 243-246;
URL: https://fundamental-research.ru/ru/article/view?id=38879 (дата обращения: 26.04.2024).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
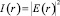 (в обозначениях работы [2]) падающего излучения:
(в обозначениях работы [2]) падающего излучения:
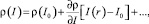 (1)
(1)
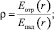
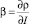 – коэффициент поверхностной нелинейности.
– коэффициент поверхностной нелинейности.
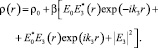 (2)
(2)

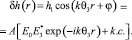 (3)
(3)
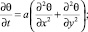 (4)
(4)
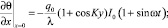
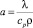 – температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
– температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
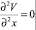 (8)
(8)
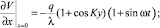
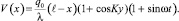 (10)
(10)
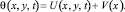 (11)
(11)
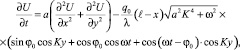 (12)
(12)
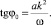
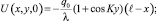
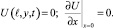 (13)
(13)
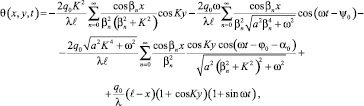
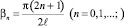
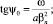
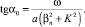
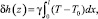 (14)
(14)
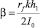 [2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
[2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
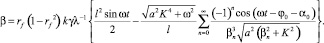 (15)
(15)



