Происходящие явления и процессы в экономике находятся в постоянной зависимости, установление взаимного влияния их друг на друга играет существенную роль для создания условий достижения необходимых экономических результатов, обеспечения эффективности деятельности предприятий, прогнозирования экономических идентификаторов в краткосрочной и долгосрочной перспективе в процессе разработки стратегического плана развития организационно-правовой структуры.
Любое экономическое явление выражается в показателях, и необходимость их взаимосвязанного изучения с учетом внутренних и внешних связей, взаимодействия и соподчиненности достигается с помощью систематизации. В настоящее время в экономической литературе рассматриваются различные виды и направления соединения показателей в систему. Одним из наиболее часто используемых способов является способ аналитического соединения взаимосвязанных показателей, при котором изучаемый процесс или явление представлены в виде суммы, частного или произведения нескольких факторов, определяющих его величину и находящихся с ним в функциональной зависимости.
Использование способа объединения показателей в систему на основе их функциональной зависимости возможно при условии, что фактор-функция полностью зависит от нескольких величин, тогда как в экономике такие связи встречаются редко. Подобных ограничений не имеет стохастическая связь, при которой разным значениям одной переменной соответствуют определенные распределения значений другой переменной. Таким образом, для создания систем взаимодействия идентификаторов хозяйственной деятельности предприятия целесообразно использовать инструментарий корреляционно-регрессионного моделирования. Использование подобных моделей на практике позволяет решить задачи прогнозирования динамики тех или иных показателей, оценки влияния факторов-аргументов на фактор-результат в среднем по совокупности.
Корреляционная связь между факторами является важнейшим частным случаем статистической связи и состоит в том, что разным значениям одной переменной соответствуют определенные средние значения другой. При этом одним из недостатков корреляционного анализа является то, что он не устанавливает причинных связей между явлениями. В данном случае возможна констатация их наличия, а причинный характер этих связей выясняется только с помощью логических рассуждений.
Разработка моделей взаимодействия экономических показателей с использованием вероятностных методов
На начальных этапах построения моделей необходимо определить факторы, непосредственно оказывающие влияние на фактор-результат, по возможности редуцировать данные, определить структуру взаимосвязи в системе. В модель включаются факторы как внешней, так и внутренней среды, оказывающие влияние на социальную, экономическую и финансовую результативность деятельности предприятия.
При прогнозировании методом корреляционно-регрессионного анализа модель включает переменные, от которых зависит поведение функции. При этом основным недостатком, по мнению автора, является то, что необходим сбор и обработка большого количества информации, но при этом остается вопрос о прогнозировании показателей работы предприятий, не вошедших в группу однородных. В целом можно отметить, что для данного метода характерна невысокая точность прогноза для отдельного хозяйствующего субъекта. Так, целесообразно количественные показатели, полученные с использованием математических методов прогнозирования, корректировать с учетом мнений экспертов.
Входные характеристики для формирования системы показателей хозяйственной деятельности предприятий сферы рекламных услуг включают в себя: единовременные и текущие затраты на создание носителя рекламной информации, в том числе и носителя в сети интернет (в данном случае затраты будут в первую очередь связаны с обслуживанием сайта и его продвижением); затраты на оплату труда персонала предприятия, систему оплаты труда менеджеров, ответственных за продажу рекламы клиентам, информацию об объемах ретроспективной и текущей деятельности конкурентов; данные общей динамики рынка; а также иной информации для планово-расчетных обоснований возможности достижения основной цели стратегического правления.
Показатели выходных результатов системы показателей могут представлять собой динамику выручки и прибыли от реализации услуг рекламного характера, а также сопутствующих товаров; рост осведомленности потенциальных потребителей о продуценте рекламных услуг; динамика рекламоспособности медианосителей, выражающаяся в таких показателях, как охват, стоимость рекламного обращения на тысячу человек, GRP и пр., а также иные экономические, социальные и финансовые эффекты хозяйственной деятельности [7].
Так, в России увеличение объема оказанных рекламных услуг в течение первого десятилетия XX века вызвано такими факторами, как рост покупательской способности населения в целом по стране; рост инвестиций, в том числе и в виде финансовых вложений в услуги рекламного характера как долгосрочный инструмент повышения результативности деятельности предприятий; увеличение количества предприятий на территории Российской Федерации, что привело к усилению конкуренции на рынке; рост цен на услуги рекламного характера; появление и развитие новых современных медианосителей (интернет-реклама) [9].
Для математического описания зависимости результативной переменной от нескольких факторных переменных используется уравнение множественной регрессии, общий вид которого представляет собой уравнение вида
Y = a + b1x1 + … + bkxk = a + ∑bjxj,
где у – среднее значение результативного признака при определенном значении факторных признаков xk; а – свободный члени уравнения; bk – коэффициенты регрессии [1].
Динамика изменения объема рекламного рынка в России может быть формализована посредством построения корреляционно-регрессионной модели, где фактор-результат (Y) – это объем рекламного рынка в России в течение заданного периода, влияющие факторы – среднедушевые денежные доходы населения (X1), объем инвестиций организационно-правовых структур (X2) и другие факторы.
Коэффициенты уравнения регрессии (bi) показывают изменение среднего по совокупности отклонения результативного признака от его средней величины при отклонении данного фактора xj (j = 1, 2) от своей средней величины на единицу его измерения при условии, что все прочие факторы, входящие в уравнение регрессии, закреплены на средних значениях. Например, при росте среднедушевых доходов населения на t руб. затраты на рекламу в стране в среднем увеличатся на m тыс. руб. при условии того, что прочие факторы, включенные в модель, остаются на своих средних значениях.
Свободный член выполняет роль доводки до функционального соотношения между средними величинами и экономического смысла не имеет. Отрицательная величина свободного члена подразумевает, что нулевые значения факторов в производстве невозможны.
Данные по динамике изменения объемов рынка рекламы, среднедушевых денежных доходов населения, объема инвестиций в основной капитал в России в течение 1996–2012 годов представлены в табл. 1.
Инвестиции в основной капитал представляют собой совокупность затрат, направленных на создание и воспроизводство основных средств (новое строительство, расширение, реконструкцию и модернизацию объектов, которые приводят к увеличению первоначальной стоимости объектов, приобретение машин, оборудования, транспортных средств, на формирование основного стада, многолетние насаждения и т.д.). Для расчета инвестиций в основной капитал на душу населения используется среднегодовая численность постоянного населения [4, 5, 6].
Таблица 1
Динамика изменения объемов рынка рекламы, среднедушевых денежных доходов населения, объема инвестиций в основной капитал в России в течение 1996–2012 годов
|
Год |
Объем рынка рекламы, млрд руб., Y |
Среднедушевые денежные доходы населения в год, тыс. руб., X1 |
Инвестиции в основной капитал на душу населения, тыс. руб., X2 |
|
1996 |
3,81 |
0,922 |
2,551 |
|
1997 |
6,72 |
1,129 |
2,782 |
|
1998 |
13,63 |
1,209 |
2,778 |
|
1999 |
15,01 |
1,956 |
4,606 |
|
2000 |
22,07 |
2,281 |
7,949 |
|
2001 |
36,50 |
3,062 |
10,308 |
|
2002 |
58,20 |
3,947 |
12,129 |
|
2003 |
74,70 |
5,167 |
15,124 |
|
2004 |
95,90 |
6,399 |
19,921 |
|
2005 |
129,20 |
8,088 |
25,232 |
|
2006 |
166,20 |
10,155 |
33,196 |
|
2007 |
217,90 |
12,540 |
46,630 |
|
2008 |
257,20 |
14,864 |
61,724 |
|
2009 |
186,40 |
16,895 |
55,887 |
|
2010 |
218,60 |
18,951 |
64,068 |
|
2011 |
263,40 |
20,755 |
77,194 |
|
2012 |
297,8 |
23,058 |
87,770 |
|
Сумма |
2063,24 |
151,38 |
529,85 |
|
Среднее |
121,37 |
8,9 |
31,17 |
|
Дисперсия |
10536 |
56,94 |
817,79 |
|
Стандартное отклонение |
102,64 |
7,54 |
28,6 |
Примечание. Таблица составлена автором на основе данных Федеральной службы государственной статистики [4, 5, 6], Российской Ассоциации рекламных агентств [2].
Показатели суммы, среднего, дисперсии, стандартного отклонения факторов рассчитаны с использованием MS Excel за 1996–2012 гг.
Для данной задачи уравнение множественной регрессии будет иметь вид:
Y = – 6 Х1 + 5,29 Х2 – 12,87. (1)
Таким образом, можно сделать вывод о том, что с 1996 по 2012 гг. объем рынка рекламы России в среднем по совокупности возрастал на 5 290 млн рублей в год при увеличении инвестиций в основной капитал на душу населения в одну тысячу рублей.
Из уравнения множественной регрессии (1) очевидно, что коэффициент регрессии при факторе X1 в уравнении (1) свидетельствует об обратной зависимости между изменениями фактора Х1 и результата Y в то время как по данным табл. 1 подобная зависимость является прямой. Таким образом, общее синергетическое влияние факторов на фактор-результат отличается от суммарного влияния факторов, если их рассматривать отдельно друг от друга. Совокупное влияние всех факторов, входящих в уравнение регрессии, не равно сумме влияния каждого из них.
Для измерения связи факторов с результативным признаком и между собой, а также для предварительного отбора факторов для включения их в уравнение регрессии целесообразно использовать матрицу парных коэффициентов корреляции.
При отборе факторов для построения корреляционно-регрессионной модели необходимо учитывать такие требования, как наличие причинной связи признаков-факторов с результативным признаком; отсутствие тесной взаимосвязи между признаками-факторами; исключение признаков-факторов, которые являются составными частями результативного признака или его функциями, а также факторов разных уровней иерархии.
Матрица парных коэффициентов корреляции для данных из табл. 1 представлена в табл. 2.
Коэффициенты регрессии выражены в разных единицах измерения и несравнимы друг с другом. Для получения сравнимых относительных показателей рассчитывают стандартизированный коэффициент регрессии или β-коэффициент:
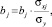
где bj – коэффициент регрессии; σx, σу – средние квадратические отклонения.
Данный βj-коэффициент при факторе xj определяет степень влияния вариации фактора xj на вариацию результативного признака y при отвлечении от сопутствующей вариации других факторов, входящих в уравнение регрессии.
Коэффициенты регрессии также могут быть выражены в виде относительных сравнимых показателях связи – коэффициентах эластичности (ej):
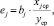
где bj – коэффициент регрессии; xjср – среднее значение фактора xj; yср – среднее значение у [5].
Данные коэффициенты показывают, на сколько результативный признак отклонится от своего среднего значения при отклонении фактора Xj от средней величины на 1 %.
На основе данных табл. 3 можно сделать вывод о том, что более значительное влияние на вариацию объема рынка рекламы в России оказывает фактор X1 – среднедушевые денежные доходы населения в год. При отклонении среднедушевых денежных доходов населения в год на 1 % или инвестиций в основной капитал на душу населения на 1 % уровень объема рекламы в России снизится на 4,4 % и повысится на 1,32 % соответственно.
Коэффициент множественной детерминации R2, характеризующий общий показатель тесноты связи всех входящих в уравнение регрессии факторов с результативным признаком, составляет для данной задачи 0,9752. Таким образом, два включенных в уравнение множественной регрессии фактора, объясняют 97 % вариации фактора-результата.
Таблица 2
Матрица парных коэффициентов корреляции (rxij)
|
Признак |
Y (объем рынка рекламы, млрд руб.) |
Х1 (среднедушевые денежные доходы населения в год, тыс. руб.) |
Х2 (инвестиции в основной капитал на душу населения, тыс. руб.) |
|
Y |
1 |
||
|
Х1 |
0,96 |
1 |
|
|
Х2 |
0,97 |
0,99 |
1 |
Таблица 3
Сравнительная сила влияния факторов-аргументов на фактор-результат (объем рынка рекламы)
|
Факторы Xj |
βj (стандартизированный коэффициент регрессии) |
Ej (коэффициент эластичности) |
|
Х1 (среднедушевые денежные доходы населения в год, тыс. руб.) |
–4,28 |
–4,4 |
|
Х2 (инвестиции в основной капитал на душу населения, тыс. руб.) |
1,4 |
1,32 |
Значения параметров многофакторной системы необходимо сопровождать вероятностными оценками и проверять их надежность, так как это необходимо для экстраполяции показателей генеральных параметров при прогнозировании развития определенной системы.
Средняя ошибка условно-чистого коэффициента регрессии bp для фактора Xp рассчитывается по формуле
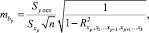
где Syост – оценка остаточного среднего квадратического отклонения результативного признака с учетом степеней свободы вариации:
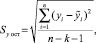
где Sxp – оценка среднего квадратического отклонения признака хр:
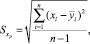
где 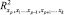 – коэффициент множественной детерминации для фактора Xp.
– коэффициент множественной детерминации для фактора Xp.
Для определения существенности влияния фактора Хр на вариацию Y расчетные значения t-критерия Стьюдента сравниваются с критическими. T-критерий Стьюдента рассчитывается по формуле [1]
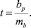
При анализе данных из табл. 4 следует, что в данной системе фактор Х1 не оказывает существенного влияния на вариацию результативного признака, по изучаемой информации связь надежно не установлена, так как расчетный t-критерий Стьюдента меньше критического даже при уровне значимости 0,1 (0,86 < 1,7613). Следовательно, модель (1) не может быть использована на практике для прогнозирования динамики факторов, а также для оценки влияния факторов друг на друга.
При анализе табл. 2 очевидно, что факторы X1 и X2 находятся в очень тесной зависимости (rxij = 0,99) и дублируют друг друга. Таким образом, в корреляционно-регрессионную модель целесообразно в данном случае было бы включить только один фактор Х2, так как он связан с фактором-результатом Y теснее, чем фактор Х1.
Таблица 4
Определение средней ошибки для параметров корреляционно-регрессионной модели (1)
|
Статистические параметры |
Коэффициенты регрессии |
|
|
b1 |
b2 |
|
|
Средняя ошибка (mbp) |
6,96 |
1,89 |
|
Расчетный t-критерий Стьюдента (tp) |
0,86 |
2,80 |
|
Критический t-критерий Стьюдента при 14 степенях свободы при уровне значимости 0,10; 0,05; 0,01. |
0,10 |
0,05 |
|
1,7613 |
2,1448 |
|
Уравнение парной регрессии, где факторным признаком являются инвестиции в основной капитал на душу населения (тыс. руб.), а результативным признаком – объем рынка рекламы (млрд руб.), имеет следующий вид:
Y = 3,68X2 + 9,16. (2)
Таким образом, можно сделать вывод о том, что в 1996–2012 гг. объем рынка рекламы России в среднем по совокупности возрастал на 3 680 млн рублей в год при увеличении инвестиций в основной капитал на душу населения в одну тысячу рублей. Коэффициент корреляции равен 0,9738.
Средняя ошибка коэффициента регрессии b2 для модели (2) составляет 0,23, расчетный t-критерий Стьюдента (tp) – 16. Критический t-критерий Стьюдента при 14 степенях свободы при уровне значимости 0,01–2,97. Следовательно, расчетное значение t-критерия Стъюдента значительно больше критического и влияние фактора X2 в модели (2) на фактор-результат существенно.
Динамику роста объема рынка интернет-рекламы в России целесообразно объяснить в рамках корреляционно-регрессионной модели, где фактор-результат (Y′) – это объем рынка интернет-рекламы в России в течение заданного периода, влияющие факторы – динамика количества пользователей сетью Интернет (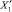 ), рост количества времени, проводимого пользователем в сети (
), рост количества времени, проводимого пользователем в сети (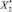 ), снижение относительных объемов рекламы в традиционных средствах массовой информации (
), снижение относительных объемов рекламы в традиционных средствах массовой информации (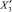 ) и другие факторы.
) и другие факторы.
Вывод
На основе анализа и обработки данных за 1996–2012 гг. сконструировано уравнение множественной регрессии, которое имеет вид
Y = – 6∙Х1 + 5,29∙Х2 – 12,87,
где Y (млрд руб.) – это объем рекламного рынка в России в течение заданного периода; X1 (тыс. руб.) – среднедушевые денежные доходы населения; X2 (тыс. руб.) – объем инвестиций организационно-правовых структур в основной капитал на душу населения.
Факторы X1 и X2 находятся в очень тесной зависимости, так как коэффициент корреляции между ними составил 0,99, и, таким образом, они дублируют друг друга. То есть в данном случае целесообразно ограничиться уравнением парной регрессии Y = 3,68 Х2 + 9,16, которое свидетельствует о том, что объем рынка рекламы в России в среднем по совокупности возрастал на 3 680 млн рублей в год при увеличении инвестиций в основной капитал на душу населения на одну тысячу рублей за исследуемый период.
Сконструированные модели возможно использовать на практике для прогнозирования динамики показателей в перспективе, оценки среднего влияния факторов друг на друга, результаты которой используются при тактическом, перспективном и стратегическом управлении предприятием. Основным ограничением прогноза на основе данной модели является условие стабильности или малой изменчивости не включенных в уравнение регрессии факторов как внешней, так и внутренней среды. Прогнозирование с использованием корреляционно-регрессионных моделей возможно лишь при условии, что в перспективе все включенные в уравнение факторы будут сохранять в среднем траекторию своего изменения.
Рецензенты:
Смирнов С.Б., д.э.н., профессор кафедры экономики и стратегического менеджмента, ФГАОУ ВПО «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики», г. Санкт-Петербург;
Кроливецкий Э.Н., д.э.н., профессор кафедры продюсирования и управления в социально-культурной сфере, ФГБОУ ВО «Санкт-Петербургский государственный институт кино и телевидения», г. Санкт-Петербург.
Библиографическая ссылка
Цуканова О.А. ИСПОЛЬЗОВАНИЕ ВЕРОЯТНОСТНЫХ МЕТОДОВ МОДЕЛИРОВАНИЯ ЭКОНОМИЧЕСКИХ СИСТЕМ ДЛЯ ОТРАСЛИ РЕКЛАМНЫХ УСЛУГ // Фундаментальные исследования. – 2015. – № 10-2. – С. 432-437;URL: https://fundamental-research.ru/ru/article/view?id=39194 (дата обращения: 27.04.2024).



