Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Коваленко А.В. 1

---

1 ФГБОУ ВПО «Кубанский государственный университет»

В работе проведен численный анализ модели ЗОМ переноса симметричного бинарного электролита с одинаковыми коэффициентами диффузии катионов и анионов. Решение краевой задачи модели ЗОМ имеет качественное и количественное соответствие с решением исходной краевой задачи для системы уравнений Нернста – Планка и Пуассона на всей области, за исключением пограничных слоев возле ионообменных мембран. При этом модель ЗОМ значительно проще и удобнее для численного и аналитического решения, поэтому она может использоваться для начального исследования переноса бинарного электролита. Модель ЗОМ может служить также эталонной задачей для определения асимптотического поведения решения исходной краевой задачи для системы уравнений Нернста – Планка и Пуассона, например, для разбиения области на части и нахождения асимптотических шкал в каждой из них.

Статья в формате PDF

1318 KB

математическое моделирование

2D-моделирование

уравнения Нернста – Планка – Пуассона

модель ЗОМ

1. Коваленко А.В., Узденова А.М., Уртенов М.Х. 2D моделирование переноса ионов соли для бинарного электролита в гальванодинамическом режиме // Экологический вестник научных центров Черноморского экономического сотрудничества. – Краснодар. ФГБОУ ВПО «Кубанский государственный университет» 2013. –№ 3. – С. 21.

2. Ньюмен Дж. Электрохимические системы. – М.: Мир, 1977. – 463 с.

3. Чубырь Н.О., Коваленко А.В., Уртенов М.Х. Двумерные математические модели переноса бинарного электролита в мембранных системах (численный и асимптотический анализ): монография. – Краснодар. ФГБОУ ВПО «КубГТУ». 2012. – 132 c.

4. Уртенов М.Х., Никоненко В.В. Анализ решения краевой задачи для уравнений Нернста – Планка – Пуассона. Случай 1:1 электролита // Электрохимия. – 1993. –Т. 29. – № 2. – С. 239.

5. Nikonenko V., Kovalenko A., Urtenov M., Pismenskaya N., Han J., Sistat P., Pourcelly G. Desalination at overlimiting currents: State-of-the-art and perspectives // Desalination. USA: Elsevier. – 2014. – № 342. – С. 85–106.

При моделировании переноса в мембранных системах в сверхпредельных токовых режимах обычно используются краевые задачи для системы уравнений Нернста – Планка и Пуассона [2]. Однако эта система уравнений сложна/

1. Она содержит 9 уравнений с 9 неизвестными функциями.

2. При естественной нормировке появляются два малых параметра ε и λ, и она становится сингулярно-возмущенной, поэтому она неудобна для численного решения.

3. Структура системы уравнений такова, что из нее можно вывести лишь модельную задачу с условием электронейтральности.

В работах [1, 3] была выведена модель ЗОМ переноса симметричного бинарного электролита с z₁ = –z₂ = 1, и равными коэффициентами диффузии катиона и аниона D₁ = D₂. В качестве такого электролита в некотором приближении можно рассматривать раствор KCl.

На рис. 1 приведена схема канала обессоливания, образованного анионообменной и катионообменной мембранами, причем y = 0 соответствует входу в канал, y = L – выходу (L = 2), x = 0 – анионообменной мембране, x = 1 – катионообменной мембране. На входе приведен профиль (эпюра) скорости течения раствора.

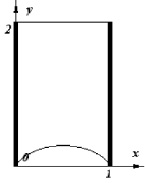
Рис. 1. Безразмерная область решения – схема канала обессоливания

Краевая задача модели ЗОМ

1. Система уравнений. Модель ЗОМ в безразмерном виде описывается относительно неизвестных функций S(x, y, t), η(x, y, t), φ(x, y, t) следующей системой уравнений:

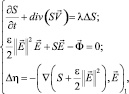(1)

где

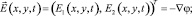
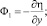
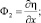
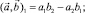
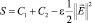– индикаторная функция (обобщенная суммарная концентрация), 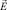– напряженность (φ – потенциал) электрического поля; C₁, C₂ – концентрация катионов и анионов; 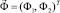– плотность тока.

Система уравнений модели ЗОМ (1) состоит из 3 уравнений с 3 неизвестными (с учетом 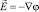), причем первое уравнение линейное, третье уравнение является условием разрешимости второго нелинейного алгебраического уравнения. Действительно, предположим, что внутри области 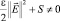, и запишем второе уравнение в виде

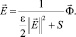
Определим двумерный аналог rot, – оператор 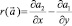. Поскольку

,

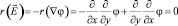то необходимым условием разрешимости является условие

,

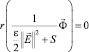откуда следует, что

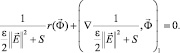
Или с учетом

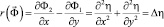
после ряда преобразований получаем уравнение

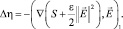
Выясним физический смысл функции S. Для этого обратим внимание на то, что при 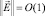имеем S = S₀ + O(ε), где S₀ = C₁ + C₂ – суммарная концентрация.

Таким образом, там, где напряженность электрического поля ограничена при ε → +0 (в области электронейтральности) S ≈ S₀ и функция S имеет смысл суммарной концентрации и является, соответственно положительной функцией. Там, где напряженность электрического поля неограничена при ε → +0 (в области пространственного заряда), функция S описывает дефект концентрации (отрицательная величина), вызванный дополнительным свехпредельным переносом ионов. Таким образом, функцию S можно назвать обобщенной концентрацией или индикаторной функцией, принимающей при сверхпредельном переносе как положительные, так и отрицательные значения, причем область, где она положительна, является асимптотически (т.е. при ε → +0) областью электронейтральности, отрицательна – областью пространственного заряда. Окрестности нулей функции S – эта промежуточная область, где происходит переход от области электронейтральности к области пространственного заряда.

2. Краевые условия. Постановки краевых условий зависят от целей конкретного исследования и могут значительно отличаться друг от друга. Ниже приведены несколько примеров краевых условий.

При постановке краевых условий нужно учитывать, что модель ЗОМ справедлива внутри области (внутри канала обессоливания за пределами погранслоев (плотной части двойного электрического слоя)), поэтому в дальнейшем x = 0 соответствует правой границе погранслоя около анионообменной мембраны, а x = 1 – левой границе погранслоя около катионообменной мембраны [1, 3]. Кроме того, нужно учитывать, что мембранные системы работают, как правило, в двух разных режимах: потенциостатическом, когда поддерживается постоянным падение потенциала, и гальваностатическом, когда ток iav, протекающий через любое сечение камеры обессоливания, является постоянным.

Как показано в [1, 3], при гальваностатическом режиме естественными являются следующие граничные условия для функции η:

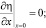
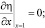(2)

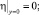
(3)

1. Граничные условия для функции S

Граничные условия на функцию S достаточно сложно определить. Ниже предлагается вариант граничного условия, в котором задаются значения обобщенной концентрации A(t, y), B(t, y) на границах x = 0, x = 1 и на входе в канал y = 0:

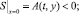
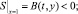(4)

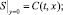
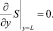(5)

Значения обобщенной концентрации A(t, y), B(t, y), C(t, x) зависят от от величины iav.

Для случая z₁ = –z₂ = 1, D₁ = D₂ распределение обобщенной концентрации симметрично, поэтому A(t, y) = B(t, y). Значения этих функций должны определяться в общем случае из сращивания решения задачи ЗОМ с решение погранслойной задачи. Для того чтобы сделать задачу ЗОМ самостоятельной зададим краевые условия независимо от погранслойной задачи. Считая функцию S(t, x, y) достаточно гладкой, получаем

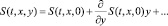
Для не слишком длинного канала:

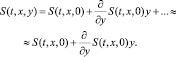
С учетом (6) получаем

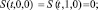
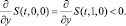
Следовательно, A(t, y) = B(t, y) = A₀(t)y, причем A₀(t) < 0.

На выходе из канала используется «мягкое» граничное условие (5), гарантирующее отсутствие вычислительных артефактов у функции S на выходе из канала.

2. Начальные условия:

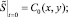
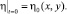(6)

Граничные и начальные условия должны быть согласованы друг с другом. Для функции η граничные условия и начальное условие будут согласованы, если взять η₀(x, y), например, в виде η₀(x, y) = –i_avy.

3. Формулы для расчета концентраций катионов и анионов

Так как [2], то с учетом C₁ + C₂ = S_0, получаем, что

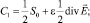
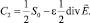
Поскольку

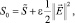
то

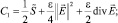
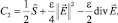
4. Анализ решений краевой задачи

4.1. Рассмотрим решение задачи ЗОМ при условиях, что рассматривается течение Пуазейля 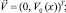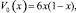и на входе предполагается практически предельное распределение концентраций, а средняя плотность тока равна предельной плотности тока i_av = 2, тогда из решения одномерной задачи [3] получаем

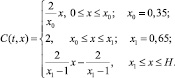
Остальные параметры имеют значения λ = 0,01,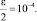

Рассмотрим результаты численных расчетов.

Из рис. 2 видно, что вниз по каналу область пространственного заряда (область, где S < 0) расширяется.

а б

Рис. 2. График обобщенной концентрации S: а – на входе; б – в канале

Из рис. 3 следует, что первая координата напряженности электрического поля значительно больше второй координаты, особенно в области пространственного заряда. Отметим, что функция η практически линейная (рис. 4), а первая координата плотности тока значительно больше второй координаты (рис. 5), т.е. фактически ток течет поперек канала.

а б

Рис. 3. Графики напряженности электрического поля: а – первой координаты; б – второй координаты

Рис. 4. График функции η

а б

Рис. 5. Графики координат плотности тока: а – первой; б – второй

Концентрация катионов возле анионообменной мембраны на входе в канал практически равна нулю и аналогично концентрации анионов возле катионообменной мембраны на входе в канал также практически равна нулю (рис. 6). В ядре потока концентрация ионов падает вниз по каналу.

а б

Рис. 6. Графики концентрации: а – катионов; б – анионов

а б в

Рис. 7. График и лиги уровня плотности заряда ρ = C1 – C2: а – график; б – линии уровня в канале; в – линии уровня вблизи анионообменной мембраны

Из рис. 7, а следует, что наибольшая плотность заряда достигается вблизи ионообменных мембран. Связано это с селективностью ионообменных мембран, причем у поверхности анионообменной мембраны плотность заряда отрицательна (C₁ << C²), а у поверхности катионообменной мембраны плотность заряда положительна (C₁ >> C₂) (рис. 6). В ядре потока условие электронейтральности выполняется с большой точностью [5].

Заключение

В работе проведен численный анализ модели ЗОМ переноса симметричного бинарного электролита с одинаковыми коэффициентами диффузии катионов и анионов. Решение краевой задачи модели ЗОМ имеет качественное и количественное соответствие с решением исходной краевой задачи для системы уравнений Нернста – Планка и Пуассона на всей области, за исключением пограничных слоев возле ионообменных мембран. При этом модель ЗОМ значительно проще и удобнее для численного и аналитического решения, поэтому она может использоваться для начального исследования переноса бинарного электролита. Модель ЗОМ может служить также эталонной задачей для определения асимптотического поведения решения исходной краевой задачи для системы уравнений Нернста – Планка и Пуассона, например для разбиения области на части и нахождения асимптотических шкал в каждой из них.

Работа выполнена при финансовой поддержке грантов РФФИ № 13-08-93105-НЦНИЛ_а, 13-08-96519 р_юг_а, 13-08-96525 р_юг_а и администрации Краснодарского края.

Рецензенты:

Халафян А.А., д.т.н., доцент, профессор кафедры прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;

Павлова А.В., д.ф.-м.н., доцент, профессор кафедры математического моделирования, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.

Библиографическая ссылка