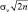Трудность решения узловых задач построения экстремальных законов распределения параметров технических систем и невозможность применения к ним обычной «классической» схемы формализма принципа максимума неопределенности (принципа максимума энтропии) связаны с тем, что для этих систем и процессов их функционирования на различных этапах жизненного цикла характерны более сложные связи между соответствующими статистическими оценками и вероятностными мерами, что порождает введение в вариационные задачи характеризации законов распределений соответствующих голономных связей. В связи с этой особенностью рассмотренная вариационная постановка задач характеризации законов распределения экстремальных случайных величин в условиях ограниченной информации отличается от традиционной наличием структурных ограничений. Это обстоятельство, в свою очередь, породило необходимость постановки и исследования новых экстремальных задач теории вероятностей и математической статистики. Особое внимание при этом было уделено методам определения множителей Лагранжа и решения нелинейных краевых задач.
Отбор изученных проблем и задач осуществлялся исходя из общей направленности работы – разработки теоретических проблем системно-информационного анализа и на его основе информационно-статистических методов формирования математических моделей объектов и процессов, изучаемых теорией технических систем. Концентрация внимания на принципах формирования моделей определяется тем значением, которое они приобретают в современной методологии научного познания закономерностей развития технических систем.
При решении специфических задач разработки и испытания технических систем неопределённость проявляется: во-первых, как неопределённость, порождаемая недостаточной полнотой, а также искажениями информации, обусловленными как внутренними факторами (сложностью структур, новизной принимаемых технических решений, трудностями передачи информации с одного уровня иерархической структуры на другой и др.), так и внешними (сложностью учёта комплекса внешних воздействий, ограничениями на объём и длительность испытаний и др.); во-вторых, как неопределённость, вызванная разнообразием условий применения и эксплуатации создаваемых и испытываемых технических систем, неопределённостью условий, в которых проявляется заложенное в конструкцию качество.
Для преодоления такого рода трудностей предложена концепция информационно-статистического подхода формирования математических моделей и разработки методов оценивания показателей качества технических систем по ограниченной информации с учётом сложного характера связей, присущих системе при её взаимодействии со средой.
В методологии экспериментальных наук интуитивно принято руководствоваться принципом Оккамы (не умножать сущности без необходимости и из двух интерпретаций одних и тех же данных выбирать более простую). Однако современное состояние естественнонаучных проблем обусловливает необходимость вероятностной интерпретации самых различных явлений. Конструктивной идеей, позволяющей преодолевать объективно существующие на этом пути трудности, является использование принципа максимума неопределенности для построения моделей редких событий [3, 6].
Когда приходится выбирать модель стохастического эксперимента, характеризующего появление какого-либо редкого события, мы располагаем, как правило, неполной информацией о схеме формирования случайной величины, являющейся моделью исхода стохастического эксперимента. Обычно известными являются лишь некоторые характеристики значения моментов (средние и дисперсные оценки). Незнание законов распределения случайных величин не исключает возможности их выбора из множества допустимых на основе использования мер неопределенности.
Приведенные ниже примеры, имеющие самостоятельное прикладное значение, иллюстрируют сущность принципа максимума неопределенности, а также необходимость постановки и исследования некоторого класса новых задач для построения экстремальных моделей редких событий [2].
Пример. Необходимо определить распределение pn = P(r = n) случайной величины r (r = 0, 1, 2, ...), если известно математическое ожидание 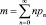 и дисперсия
и дисперсия 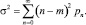
Решение. Для того чтобы найти вероятность pn, необходимо решить следующую задачу:
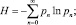
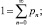
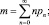
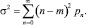
С этой целью введем неопределенные множители Лагранжа ?i (i = 0, 1, 2) и исследуем на экстремум следующую функцию:
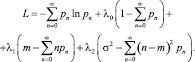
Поскольку
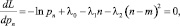
то
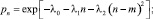
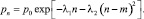
Полученное выражение для распределения r является дискретным аналогом нормального распределения [7, 8].
Далее рассмотрим класс задач, формально описываемых следующей схемой. Пусть параметр закона Пуассона ? является случайной величиной. Случайный характер параметра ? может быть обусловлен нарушением стационарности пуассоновского потока, засорением генеральной совокупности, ограниченностью исходной информации о среднем значении числа событий за заданный промежуток времени и др. Пусть о случайной величине известны: математическое ожидание mv и величина центрального момента второго порядка (дисперсия 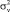 ) [1, 9, 10]. Пусть область возможных значений случайной величины можно считать практически неограниченной (–? < v < ?). Это обстоятельство предполагает справедливость условия ?v << mv, практически mv > 3?v. Пусть наблюдается достаточно большое число случайных событий r (r > 10), однако реализуемым (наблюдаемым) является последнее событие n. В условиях рассматриваемого стохастического эксперимента естественным образом возникает необходимость выбрать закон распределения вероятностей p(v) и ввести в рассмотрение новую модификацию закона Пуассона (построения модели «сверхредких» событий) [2].
) [1, 9, 10]. Пусть область возможных значений случайной величины можно считать практически неограниченной (–? < v < ?). Это обстоятельство предполагает справедливость условия ?v << mv, практически mv > 3?v. Пусть наблюдается достаточно большое число случайных событий r (r > 10), однако реализуемым (наблюдаемым) является последнее событие n. В условиях рассматриваемого стохастического эксперимента естественным образом возникает необходимость выбрать закон распределения вероятностей p(v) и ввести в рассмотрение новую модификацию закона Пуассона (построения модели «сверхредких» событий) [2].
Можно сказать, что экстремальным распределением (распределением, обладающим энтропией при определенных выше ограничениях и условиях) является предельное гипернормальное распределение (экстремальное распределение II типа) [4, 5].
Математическое ожидание производящей функции определяется следующим образом

где учитывается маргинальное распределение параметра ?, квантильная функция которого имеет вид
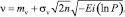
По производящей функции распределения по формуле
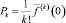
находим новую модификацию распределения Пуассона
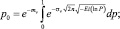
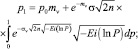
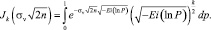
Полученные выражения дают возможность для расчета вероятностей сверхредких событий. Значения этих интегралов представлены в таблице.
Численные значения интеграла 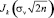
|
k
|
0,0 |
1,0 |
2,0 |
3,0 |
4,0 |
|
0,0 |
1,0 |
0,686 |
0,641 |
0,702 |
0,836 |
|
0,01 |
0,993 |
0,679 |
0,634 |
0,693 |
0,826 |
|
0,05 |
0,966 |
0,655 |
0,60 |
0,662 |
0,786 |
|
0,1 |
0,934 |
0,625 |
0,545 |
0,624 |
0,738 |
|
0,25 |
0,847 |
0,546 |
0,489 |
0,522 |
0,613 |
|
0,5 |
0,724 |
0,438 |
0,376 |
0,391 |
0,451 |
|
0,75 |
0,626 |
0,355 |
0,291 |
0,293 |
0,333 |
|
1,0 |
0,545 |
0,291 |
0,227 |
0,222 |
0,246 |
|
1,25 |
0,479 |
0,241 |
0,178 |
0,168 |
0,183 |
|
1,5 |
0,424 |
0,201 |
0,141 |
0,129 |
0,136 |
|
2,0 |
0,539 |
0,144 |
0,091 |
0,077 |
0,077 |
|
3,0 |
0,230 |
0,081 |
0,042 |
0,030 |
0,026 |
|
4,0 |
0,166 |
0,050 |
0,022 |
0,013 |
0,010 |
|
5,0 |
0,125 |
0,034 |
0,012 |
0,008 |
0,004 |
|
6,0 |
0,102 |
0,024 |
0,080 |
0 |
0 |
|
8,0 |
0,061 |
0,013 |
0 |
0 |
0 |
|
10,0 |
0,040 |
0,008 |
0 |
0 |
0 |
|
12,0 |
0,027 |
0,005 |
0 |
0 |
0 |
|
15,0 |
0,015 |
0,003 |
0 |
0 |
0 |
Вывод
Анализ совокупности научно-технических проблем, возникающих в процессе научных исследований сложных информационных систем, позволяет сделать вывод, что большинство из них связано с постановкой и решением ряда нетривиальных задач. Процедуры постановки и решения этих задач затрагивают целый ряд областей фундаментального и прикладного значения. При формальном использовании традиционных методов статистической обработки данных можно получить ошибочные заключения. Все это приводит к идее широкого применения информационно-статистических методов (принципа максимума неопределенности).
Объективная потребность использования информационно-статистических методов, системно-информационного анализа позволила придать выявленным закономерностям развития технических систем количественно-качественное содержание и обеспечить их статистическую (вероятностную) интерпретацию.
– рассмотрено применение принципа максимума неопределённости при построении распределения крайней порядковой статистики (максимального значения из случайной последовательности) по ограниченной информации об исходном распределении;
– показано чёткое разграничение условий применения нормального и гипернормального экстремальных распределений;
– рассмотрены модели редких событий для принципиально новых технических решений.
Рецензенты:
Музаев И.Д., д.т.н., профессор, Финансовый университет при Правительстве Российской Федерации (Финуниверситет), г. Владикавказ;
Дзагоева М.Р., д.э.н., профессор, Финансовый университет при Правительстве Российской Федерации (Финуниверситет), г. Владикавказ.