Переход к параллельной обработке данных сделал организацию вычислений объектом исследований, характеризующимся множеством вариантов. Для выполнения таких исследований необходим формальный инструмент, способный описать их разнообразие. Базой для разработки такого инструмента является множество алгоритмов, описывающих организацию последовательных вычислений. Реализуя переход от алгоритма к модели, можно создать такой инструмент. Путь реструктуризации [1, 2, 7] известных последовательных алгоритмов и их программ, пройденный для изучения вопросов построения параллельных алгоритмов, не привел к созданию общего формального описания – модели организации вычислений. Для погружения последовательных алгоритмов в пространственно-временную среду необходимо выделить то их общее свойство, которое может быть использовано для выявления единого правила такого погружения. Таким свойством является композиционность. Именно установление формальных законов образования композиционных форм в работе [8] связывается с получением возможности повышения эффективности параллельных вычислений. Действительно, установив такие законы, можно на их основе синтезировать различные варианты организации вычислений, предназначенные для выполнения одной и той же операции, и оценивать аппаратурно-временную сложность их реализации. Эти возможности, в свою очередь, позволяют выполнять совместное проектирование алгоритмов и архитектур, представляющее собой современное направление [9, 10] создания перспективных высокопроизводительных вычислительных систем.
Данная статья посвящена представлению модели организации вычислений для операций цифровой обработки сигналов (ЦОС), полученной на основе разработанного закона описания внутренней структуры их последовательных алгоритмов [3–5, 11]. Этот закон позволил реализовать переход от алгоритма к модели, путем построения композиционных форм, ориентированных на синтез параллельных алгоритмов.
Разнообразие вариантов организации вычислений и его формальное описание
Подойдем к представлению новой модельной формы описания структур алгоритмов, изначально ориентированной на параллельную обработку, отталкиваясь от объекта описания, коим является организация параллельных вычислений. Этот объект характеризуется разнообразием вариантов, следовательно, модель должна его описывать. На основе модели можно выполнять параметризованный синтез и анализ вариантов организации вычислений, а также управлять изменениями их структур. Такие возможности разработанной модели делают её основой для реализации совместных исследований алгоритмов и архитектур. Эти исследования, выполняемые в процессе совместного проектирования алгоритмов и архитектур, позволяют сделать обоснованным выбор варианта организации вычислений. На самом деле, проблема выбора является порождением разнообразия вариантов, следовательно, получив инструмент для его описания, мы тем самым создадим основу для реализации обоснованного выбора. На рисунке представлена укрупненная схема совместных исследований алгоритмов и архитектур. Схема представляет симбиоз компонентов, обеспечивающий обоснованный выбор вариантов. Схема носит итеративный характер. Совместное исследование алгоритмов и архитектур предполагает одновременный анализ параметров синтезируемых алгоритмических вариантов и параметров изучаемых архитектур и приводит к получению оценок аппаратурно-временной сложности реализации формируемых при этом решений. Выбор наилучших решений из множества осуществляется на основе заданных оптимизационных критериев реализации вычислений. Основной компонентой схемы, обеспечивающей её функционирование, является разработанная модель. Для построения модели была исследована внутренняя структура входных данных и операций ЦОС, в результате чего был установлен закон её описания. На основе этого закона данные и операции были представлены с помощью композиционных форм данных (КФД) и композиционных форм операций (КФО). В обобщенном виде созданная модель организации вычислений может быть представлена с помощью следующей формулы:
КФД + КФО = Модель.
Суть закона описания внутренней структуры данных и операций состоит в использовании многомасштабного представления этих структур. Для реализации закона были разработаны формальные инструменты – методология декомпозиции данных и методика синтеза композиционных форм операций. В работах [6, 12, 13] была представлена схема перехода от алгоритма к модели, базирующаяся на использовании этих инструментов. Выполненный переход от обычных форм к композиционным позволил говорить об эволюции формальных основ для описания организации вычислений [13], позволившей качественно изменить эти основы, подняв их на более высокий уровень абстракции. Таким образом, привычный алгоритм был заменен моделью, описывающей требуемое разнообразие структур параллельных алгоритмов. Эволюционный характер выполненного перехода свидетельствует о преемственности новых и исходных форм для представления операций ЦОС, формально проявляющейся в установленной параметрической зависимости между указанными формами. Эта зависимость связана с проявлением закона описания внутренней структуры алгоритмов для класса операций ЦОС. Основной характеристикой этого закона является параметризация структуры алгоритма. Введя для N-точечной операции ЦОС (свертки, корреляции, дискретного преобразования Фурье (ДПФ) и других ортогональных преобразований) параметр L, показывающий степень сжатия указанной операции во временной области до размера h1 = N/L, можно для выбранной операции синтезировать разнообразие структур параллельных алгоритмов на основе закона описания внутренней структуры исходного последовательного алгоритма. При этом значение параметра L = 1 соответствует последовательному алгоритму, а все возможные значения параметра L ≠ 1 формируют необходимое разнообразие вариантов организации вычислений для выбранной операции.
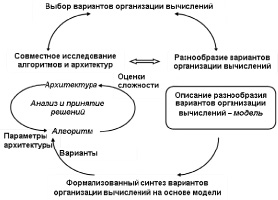
Укрупненная итеративная схема совместных исследований алгоритмов и архитектур, обеспечивающих обоснованный выбор вариантов организации вычислений
Завершая данный параграф, приведем следующее модельное описание алгоритмов Ai(t) – 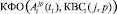 . Компонентами этого описания являются алгоритмы
. Компонентами этого описания являются алгоритмы 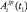 , полученные в результате декомпозиции, погружения в пространственную среду, характеризуемую параметрами j, p (j, p = 0, …, L – 1), и сжатия во времени до размера h1 (t1 = 0, …, h1 – 1) последовательных алгоритмов Ai(t) (t = 0, …, N –1), а также координационно-вычислительные среды КВСi(j, p). Тогда множество последовательных алгоритмов
, полученные в результате декомпозиции, погружения в пространственную среду, характеризуемую параметрами j, p (j, p = 0, …, L – 1), и сжатия во времени до размера h1 (t1 = 0, …, h1 – 1) последовательных алгоритмов Ai(t) (t = 0, …, N –1), а также координационно-вычислительные среды КВСi(j, p). Тогда множество последовательных алгоритмов 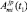 , разработанных для различных операций Оm, благодаря созданному механизму образования КФО, будет компонентой модельного описания для целого класса алгоритмов. Ключевым параметром, сформированного таким образом модельного описания
, разработанных для различных операций Оm, благодаря созданному механизму образования КФО, будет компонентой модельного описания для целого класса алгоритмов. Ключевым параметром, сформированного таким образом модельного описания
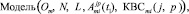
определяющим возможность и уровень сжатия вычислений во времени, является параметр L, задаваемый следующим образом: L = N/h1. Именно введение и использование этого параметра позволило установить связь между алгоритмическим и модельным описаниями организации вычислений.
Методика совместного проектирования алгоритмов и архитектур
Совместное проектирование алгоритмов и архитектур, основанное на изменениях с целью оптимизации как архитектурных, так и алгоритмических параметров создаваемых систем, характеризуется реализацией общей методологии сверху – вниз – от алгоритма к архитектуре. Внедрение такой общей методологии в процесс проектирования позволяет поднять его на более высокий уровень абстракции, понять и оценить ожидаемую архитектуру, а также оценить все пространство проектирования, т.е. все возможные варианты проектирования. Это, в свою очередь, создает основу для реализации обоснованного выбора наилучшего варианта, обеспечивая тем самым эффективность параллельной обработки.
Разработанная модель организации вычислений для операций ЦОС может стать основой для реализации вышеназванной методологии проектирования. На основе предложенной модели была разработана общая методика совместного проектирования алгоритмов и архитектур, характеризующаяся совместной оптимизацией их параметров. Методика представляет проектирование в виде итеративного процесса, генерирующего и оценивающего различные варианты организации вычислений на основе совместных исследований алгоритмов и архитектур. Реализация такого процесса позволит на алгоритмическом уровне выявлять варианты, наилучшим образом удовлетворяющие проектным условиям. Основными шагами разработанной методики являются доопределение модели архитектурными параметрами и формирование параметрических зависимостей оценок аппаратурно-временной сложности реализации исследуемых вариантов. На основе такой доопределенной модели может быть реализован итеративный этап совместных исследований алгоритмов и архитектур, каждая итерация которого характеризуется синтезом, оценкой и анализом рассматриваемых вариантов. Внедрение такого этапа в процесс проектирования позволит повысить эффективность параллельной обработки, следовательно, этап должен стать неотъемлемой частью проектирования высокопроизводительных вычислительных систем.
Заключение
Представленная формальная модель позволяет описывать разнообразие вариантов организации вычислений для операций ЦОС, выполнять их синтез и анализ, а также управлять изменениями их структур. Модель является архитектурно-независимой и способной обеспечить реализацию обоснованного выбора варианта параллельной организации вычислений. Такой выбор может быть осуществлен в процессе выполнения этапа совместных исследований алгоритмов и архитектур. Предложенный путь реализации выбора позволяет повысить эффективность параллельной обработки за счет согласования архитектурных и алгоритмических параметров проектируемых вычислительных систем. Возможность реализации такого проектирования, основанного на совместной оптимизации алгоритмических и архитектурных параметров и отвечающего современным тенденциям развития данной области, обеспечивается свойствами разработанной модели.
Работа выполнена при частичной поддержке программы УрО РАН «Математические модели, алгоритмы, высокопроизводительные вычислительные и информационные технологии и приложения» (проект 15-7-1-20).
Библиографическая ссылка
Климова О.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОРГАНИЗАЦИИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ ДЛЯ ОПЕРАЦИЙ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ // Фундаментальные исследования. – 2015. – № 11-7. – С. 1328-1331;URL: https://fundamental-research.ru/ru/article/view?id=39833 (дата обращения: 26.04.2024).



