В работах [1, 8, 11] рассматривалась проблематика моделирования динамики «затраты - выпуск» для предприятия с неоклассической производственной функцией. На основе динамической модели денежных и материальных потоков производственной сферы предприятия, корректно описываемой неоклассической производственной функцией, авторам удалось выделить эндогенные параметры γt и βt (доли соответственно собственных инвестиций в конечном продукте предыдущего планового периода и заемных средств в совокупных инвестициях производственной сферы текущего периода) этой сферы, существенно влияющие на качество принимаемых в этой сфере решений. Авторами получены новые результаты, существенно обогатившие неоклассическую производственную теорию. Например, тезис о том, что масштаб производства (степень однородности производственной функции) является основным экзогенным параметром в сочетании с управляемыми параметрами γt и βt определяющим величину денежных и материальных потоков и экономическую динамику производственной сферы предприятия, с учетом эффектов финансового и операционного рычагов.
Существенной особенностью цитируемой и аналогичных неоклассических моделей является, однако, значительное упрощение учитываемых в них формальных критериев и ограничений деятельности предприятия в условиях рыночной экономики. Так, например, не учитываются факторы волатильности товарных и финансовых рынков, условия принятия управленческих решений в условиях риска и др. [3, 4]. Основным упрощением является неполный учет налоговой нагрузки предприятия [6, 7]. Этот недостаток моделей Д.Безухова - М.Халикова и Р.Расулова - М.Халикова [1, 8] мы попытались преодолеть в этой работе.
Рассмотрим постановку задачи и результаты моделирования экономической динамики предприятия с учетом оттока налоговых платежей для важного частного случая, когда зависимость между выпуском и затратами задается неоклассической производственной функцией степени однородности α (α>0).
Фиксируем следующие экзогенные параметры производительной и финансовой сфер предприятия:
1) ставки τНДС, τЕСН, τНИ, τНПР – ставки налогов соответственно: на добавленную стоимость, страховых взносов (единый социальный налог), на имущество и на прибыль;
2) процентные ставки 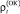 и
и 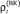 на заемный капитал (по отдельным интервалам с шагом планирования), инвестированный на шаге t соответственно в оборотные и внеоборотные активы;
на заемный капитал (по отдельным интервалам с шагом планирования), инвестированный на шаге t соответственно в оборотные и внеоборотные активы;
3) μ(t) – норматив амортизационных отчислений для периода t.
Детерминантами модели являются показатели используемой технологии: α – степень однородности функции [2, 10]; с(1) – удельные затраты; θt – доля фонда оплаты труда в оборотных активах.
Управляемые параметры для интервала планирования t задаются νt, γt, βt – доли соответственно: инвестиций в оборотные активы (всовокупных инвестициях в производственную сферу), собственных инвестиций в конечном продукте предыдущего планового периода, заемных средств в совокупных инвестициях в производственную сферу.
Для предприятия с неоклассической производственной функцией степени однородности α, для которой зависимость в паре «выпуск - затраты» задаётся соотношением [10]:
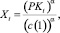 (1)
(1)
где Xt – величина выпуска для периода t; PKt=c(Xt) – совокупные затраты на объём выпуска Xt, а именно оборотный производственный капитал; с(1) – удельные затраты.
Промежуточный продукт TRt (встоимостном выражении) получим умножением величины выпуска на цену реализации продукта.
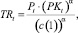 (2)
(2)
где PKt – производственный капитал, сформированный в начале периода t и направляемый на финансирование операционной деятельности этого периода:
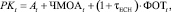 (3)
(3)
где At – амортизация; ЧМОАt – чистые материальные оборотные активы с учетом НДС:
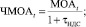
ФОТt – фонд оплаты труда.
Учитывая технологически обоснованную долю θt ФОТt в оборотных активах производственной сферы для периода t, представим (3) в виде
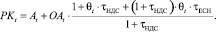 (4)
(4)
Восстановленная стоимость оборотных активов, которая в составе себестоимости включается в стоимость реализации продукции и освобождается от налогообложения, учитывается в инвестиционных потоках в оборотные активы следующего интервала планирования:
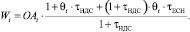 (5)
(5)
Оборотные активы предприятия для периода планирования t можно представить в виде суммы инвестиций, из конечного продукта периода t – 1, заемных средств, направляемых в оборотные активы в начале текущего периода, и восстановленной стоимости. Будем предполагать, что оборотный капитал производственной сферы и амортизация основного капитала полностью (без остатка) покрывают затраты основной производственной деятельности. Вэтом случае
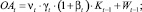 (6)
(6)
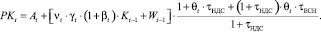
После выплаты обременений (обязательств перед поставщиками, работниками и государством) остаточный продукт составит величину:
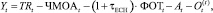 (7)
(7)
где
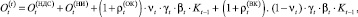 (8)
(8)
где
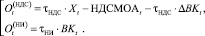 (9)
(9)
В конечном продукте учитывается амортизация, выплаты кредиторам и налог на прибыль:
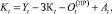 (10)
(10)
где 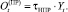 (11)
(11)
Составляющие денежных потоков производственной сферы предприятия на последовательных шагах (t – 1) и t связаны следующими рекуррентными соотношениями:
–собственные инвестиции предприятия определяются долей γt в конечном продукте предыдущего планового периода, которая является управляемым параметром:
It=γt•Kt–1; (12)
–вначале шага t определяется величина заемных средств в совокупных инвестициях в производственную сферу (по доле βt):
ЗKt=βt•γt•Kt–1. (13)
Доля (1 – vt) заемного капитала инвестируется во внеоборотные активы:
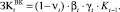 (14)
(14)
Изменение внеоборотного капитала на шаге t, обусловленное инвестициями из всех учитываемых источников:
ΔBKt=(1 – νt)•γt•(1+βt)•Kt–1. (15)
Учитывая дополнительные изменения внеборотного капитала на шаге t (амортизация и модернизация), оценим его совокупный объем:
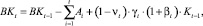 (16)
(16)
где 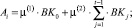 (17)
(17)
–остальные рекуррентные соотношения задаются следующими выражениями:
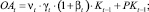 (18)
(18)
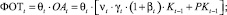 (19)
(19)
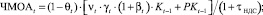 (20)
(20)
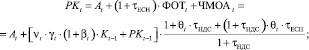 (21)
(21)
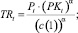 (22)
(22)
где 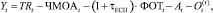 (23)
(23)
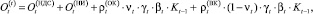 (24)
(24)
где
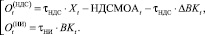 (25)
(25)
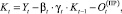 (26)
(26)
где 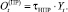 (27)
(27)
Конечный продукт распределяется на текущее потребление (дивиденды) и инвестиции в производственную сферу следующего периода:
Kt=It+Dt=γt+1•Kt+(1 – γt+1)•Kt. (28)
Исследования экономической динамики предприятия с нелинейной неоклассической производственной функцией основаны на модели, задаваемой соотношениями (12)–(28).
Практические расчеты динамики производственной сферы предприятий с неоклассической производственной функцией для случаев убывающей (α<1) и возрастающей (α>1) отдачи от масштаба производства и различных комбинаций регулируемых параметров γt, и βt проведены для следующих рыночных и технологических констант: τЕСН=0,3, τНДС=0,18, τНИ=0,002, τНПР=0,2 [5], P=800, ρ(ОК) =0,0175, ρ(ВК) =0,01, θ=0,03, ν=0,9, c(1)=250; налоговые и процентные ставки рассчитаны в предположении, что один период соответствует одному календарному месяцу. Предположим, что в нулевом периоде внеоборотный капитал ВК0 равен 300000тыс. руб., оборотные активы ОА0 – 20000тыс.руб. (табл.1).
Наиболее интересны результаты для предприятий с масштабом производства α=0,83 (по нашим данным к предприятиям с подобной суммарной эластичностью выпуска относятся большинство предприятий обрабатывающей промышленности и машиностроительные предприятия с мелкосерийным производством [9]), (табл.2).
Таблица 1
Варианты расчетов экономической динамики предприятия с неоклассической производственной функцией для различных значений параметров α, γt и βt
|
α |
γt |
βt |
Характер динамики «выпуск - затраты» |
|
0,8 |
0,1 |
0,1 |
Незначительное квазилинейное падение |
|
0,8 |
0,1 |
0,5 |
Медленное квазилинейное падение с меньшим конечным продуктом |
|
0,8 |
0,1 |
0,9 |
Незначительное экспоненциальное падение с меньшим конечным продуктом |
|
0,8 |
0,5 |
0,1 |
Умеренное экспоненциальное падение |
|
0,8 |
0,5 |
0,5 |
Умеренное экспоненциальное падение с незначительными колебаниями и меньшим конечным продуктом |
|
0,8 |
0,5 |
0,9 |
Умеренное экспоненциальное падение с колебаниями и меньшим конечным продуктом |
|
0,8 |
0,9 |
0,1 |
Экспоненциальное падение |
|
0,8 |
0,9 |
0,5 |
Экспоненциальное падение с колебаниями и меньшим конечным продуктом |
|
0,8 |
0,9 |
0,9 |
Экспоненциальное падение с сильными колебаниями и меньшим конечным продуктом |
|
1,2 |
γt |
βt |
Заметный экспоненциальный рост, увеличивающийся с ростом параметров γt, и βt |
Таблица 2
Варианты расчетов экономической динамики предприятия с масштабом производства α=0,83 для различных
γt, βt и νt
|
α |
γt |
βt |
νt |
Динамика «выпуск -затраты» |
|
1 |
2 |
3 |
4 |
5 |
|
0,83 |
0,1 |
0,1 |
0,9 |
Квазилинейный рост |
|
0,83 |
0,1 |
0,1 |
0,1 |
Аналогичный квазилинейный рост конечного продукта при меньшем объеме производства |
|
0,83 |
0,1 |
0,5 |
0,9 |
Незначительно более быстрый экспоненциальный рост с меньшим конечным продуктом |
|
0,83 |
0,1 |
0,9 |
0,9 |
Более быстрый экспоненциальный рост с меньшим конечным продуктом (табл.3, рис.1) |
|
0,83 |
0,1 |
0,9 |
0,1 |
Аналогичный экспоненциальный рост при меньшем объеме производства |
|
0,83 |
0,5 |
0,1 |
0,9 |
Экспоненциальный рост |
|
0,83 |
0,5 |
0,1 |
0,1 |
Квазилинейный рост конечного продукта, приводящий к большему результату, при меньшем объеме производства |
|
0,83 |
0,5 |
0,5 |
0,9 |
Более быстрый экспоненциальный рост в начале периода с незначительными колебаниями |
|
0,83 |
0,5 |
0,5 |
0,1 |
Квазилинейный рост конечного продукта практически без колебаний, приводящий к большему результату при меньшем объеме производства |
|
0,83 |
0,5 |
0,9 |
0,9 |
Более быстрый экспоненциальный рост в начале периода с колебаниями (табл.4, рис.2) |
|
0,83 |
0,5 |
0,9 |
0,1 |
Квазилинейный рост со сглаженными колебаниями в начале периода (табл.5, рис.3) |
|
0,83 |
0,9 |
0,1 |
0,9 |
Угасающий экспоненциальный рост |
|
0,83 |
0,9 |
0,5 |
0,9 |
Угасающий экспоненциальный рост с колебаниями и меньшим конечным продуктом |
|
0,83 |
0,9 |
0,9 |
0,9 |
Угасающие колебания и меньший конечный продукт (табл.6, рис.4) |
|
0,83 |
0,9 |
0,9 |
0,1 |
Экспоненциальный рост со сглаженными колебаниями в начале периода (табл.7, рис.5) |
Таблица 3
α=0,83; γt=0,1; βt=0,9; νt=0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
21636 |
11645 |
1,92 % |
|
2 |
25387 |
12195 |
2,12 % |
|
3 |
28664 |
12605 |
2,27 % |
|
4 |
31521 |
12924 |
2,40 % |
|
5 |
34011 |
13177 |
2,51 % |
|
6 |
36177 |
13378 |
2,61 % |
|
7 |
38062 |
13542 |
2,69 % |
|
8 |
39701 |
13676 |
2,77 % |
|
9 |
41126 |
13788 |
2,85 % |
|
10 |
42364 |
13881 |
2,92 % |
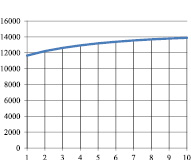
Рис. 1. Kt при α=0,83; γt=0,1; βt=0,1; νt=0,9
Таблица 4
α=0,83; γt=0,5; βt=0,9; νt=0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
29599 |
7382 |
2,21 % |
|
2 |
36702 |
10244 |
2,39 % |
|
3 |
44935 |
9577 |
2,55 % |
|
4 |
51549 |
10226 |
2,63 % |
|
5 |
57736 |
10178 |
2,69 % |
|
6 |
63044 |
10345 |
2,72 % |
|
7 |
67754 |
10360 |
2,74 % |
|
8 |
71837 |
10404 |
2,75 % |
|
9 |
75403 |
10410 |
2,77 % |
|
10 |
78495 |
10417 |
2,78 % |
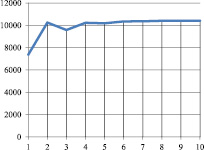
Рис. 2. Kt при α=0,83; γt=0,5 βt=0,9 νt=0,9
Таблица 5
α=0,83; γt=0,5 βt=0,9 νt=0,1
|
t |
PKt |
Kt |
ROEt |
|
1 |
21594 |
7683 |
2,31 % |
|
2 |
25193 |
9883 |
2,25 % |
|
3 |
28593 |
9689 |
2,42 % |
|
4 |
31667 |
10233 |
2,47 % |
|
5 |
34517 |
10470 |
2,53 % |
|
6 |
37158 |
10770 |
2,56 % |
|
7 |
39627 |
11016 |
2,59 % |
|
8 |
41950 |
11255 |
2,60 % |
|
9 |
44149 |
11476 |
2,61 % |
|
10 |
46246 |
11688 |
2,61 % |
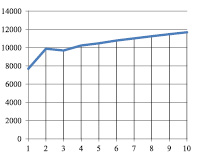
Рис. 3. Kt при α=0,83; γt=0,5 βt=0,9 νt=0,1
Таблица 6
α=0,83; γt=0,9 βt=0,9 νt=0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
36804 |
3748 |
2,42 % |
|
2 |
42453 |
10967 |
2,46 % |
|
3 |
56893 |
5910 |
2,64 % |
|
4 |
62655 |
10116 |
2,62 % |
|
5 |
73208 |
6892 |
2,64 % |
|
6 |
78050 |
9483 |
2,60 % |
|
7 |
85674 |
7359 |
2,57 % |
|
8 |
89452 |
9014 |
2,53 % |
|
9 |
94921 |
7590 |
2,50 % |
|
10 |
97771 |
8674 |
2,47 % |
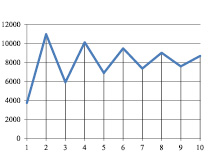
Рис. 4. Kt при α=0,83; γt=0,9 βt=0,9 νt=0,9
Таблица 7
α=0,83; γt=0,9 βt=0,9 νt=0,1
|
t |
PKt |
Kt |
ROEt |
|
1 |
22395 |
4556 |
2,68 % |
|
2 |
26091 |
9962 |
2,23 % |
|
3 |
30194 |
7339 |
2,65 % |
|
4 |
33641 |
9510 |
2,50 % |
|
5 |
37141 |
8713 |
2,64 % |
|
6 |
40319 |
9677 |
2,58 % |
|
7 |
43454 |
9536 |
2,61 % |
|
8 |
46419 |
10042 |
2,57 % |
|
9 |
49327 |
10133 |
2,56 % |
|
10 |
52141 |
10461 |
2,52 % |
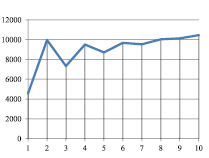
Рис. 5. Kt при α=0,83; γt=0,9 βt=0,9 νt=0,1
На основе проведенных по модели (12)–(28) расчетов с использованием значений параметров из табл.1 и 4 были получены результаты динамики «затраты – выпуск», представленные на рис.1–5. Анализ моделируемой динамики позволил сформулировать следующие выводы.
1.Нерегулируемый параметр α – масштаб производства – оказывает определяющее влияние на эффективность производственной сферы предприятия, что в полной мере корреспондируется с безналоговой моделью [1, 8].
2.Управляемые параметры γt и βt оказывают существенное влияние на моделируемую динамику: воздействуя на эти параметры, можно замедлить или, наоборот, ускорить падение/рост, изменить средний на интервале результат производства, однако нельзя изменить отрицательную динамику на положительную, что существенно отличается от результата, полученного для безналоговой модели [1, 8].
3.Управляя долей νt инвестиций в оборотный капитал, можно продлить период роста и сгладить колебания результата, в случае затухающего роста и большого объема заемного капитала. Таким образом, манипулирование этим параметром в условиях использования в инновациях накопленной амортизации даже при низком начальном объеме производства способствует нивелированию отрицательного денежного потока налоговых выплат.
Библиографическая ссылка
Приображенская В.В., Рыжова А.В. МОДЕЛИРОВАНИЕ ДИНАМИКИ «ЗАТРАТЫ – ВЫПУСК»ДЛЯ ПРЕДПРИЯТИЯ С НЕОКЛАССИЧЕСКОЙ ПРОИЗВОДСТВЕННОЙ ФУНКЦИЕЙ С УЧЕТОМ НАЛОГООБЛОЖЕНИЯ // Фундаментальные исследования. – 2016. – № 5-3. – С. 627-633;URL: https://fundamental-research.ru/ru/article/view?id=40354 (дата обращения: 26.04.2024).



