Приемы формализации на базе алгебры конечных предикатов оказались удобным средством оптимизации конечных объектов и процессов, оперирующих символьной информацией [1]. Эффективность этого аппарата в области теории искусственного интеллекта показана в [2].
В теории конечных предикатов известен ряд результатов по декомпозиции предикатов, т.е. взаимно однозначного преобразования предикатов одной размерности в предикаты другой размерности. При моделировании информационных объектов и процессов преобразование системы предикатов, имеющих произвольную конечную размерность, в систему бинарных предикатов дает ряд преимуществ. Основным из них оказывается возможность перехода от последовательного алгоритмического вычисления к параллельному, что очень важно при решении задач с больших объемов вычислений. Логической сетью называется графическое представление системы бинарных предикатов. Вершинам графа соответствуют предметные переменные xi с областью определения Ai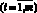 
, а дугам – бинарные предикаты K(xi, xj).
Аппарат, рассматриваемый в данной статье, ориентирован на решение задач идентификации структур в области искусственного интеллекта [1, 2]. Традиционные логические сети не предназначены для обработки структур, которые могут отражать выполнение процессов произвольной физической природы (поиска данных в сети интернет, процессы мышления и т.п.), по причине обязательного направления во времени. Эти процессы можно представить в виде последовательности событий, каждое из которых обладает временной меткой. В данном случае важно не абсолютное значение, задаваемой временной меткой, а порядок событий [6].
Другое перспективное приложение подобного аппарата связано с автоматизацией алгебраического метода синтеза линейных систем автоматического управления [7, 9]. Процесс нахождения оптимальных и субоптимальных расположений полюсов таких систем представляет собой разветвленную логическую схему, частично иерархизированную необходимостью последовательного выполнения определенных фаз, на которых допускается параллельное выполнение подобных процедур, часто включающих рекурсивные и циклические последовательности подпроцессов.
В связи с вышеизложенным возникает проблема предикатного описания процессов произвольной физической или технической природы на основе логических сетей, рассмотрению которой и посвящена данная работа.
Способы построения моделей и модифицированная логическая сеть
Методика построения и настройки модели гибкого процесса подробно описаны в [8]. Проанализированы особенности этапа адаптации модели [3, 8].
Предложена предикатная процессная модель на основе дерева процессов и аппарата конечных предикатов [4]. Предложенный метод позволяет объединить базовые способы слияния логов и построения модели процесса средствами process mining. Были введены два типа вершин логической сети. В приведенных работах рассмотрено общее представление графа процесса, однако вопросы моделирования таких процессов логической сетью требуют дальнейшего развития.
Вводя в конструкцию логической сети операции, рассмотренные в [3, 8], мы уходим от общепринятого определения логической сети, как системы бинарных предикатов. Во-первых, логическая сеть – это неориентированный граф, а полученная нами конструкция – ориентированный граф. Во-вторых, мы используем не только бинарные предикаты, но и тернарные. Это основное отличие, в полученной конструкции используются операции над предикатами, т.е. предикаты второго порядка [5, 8]. Назовем такую сеть логической сетью с бинарными предикатными операциями, поскольку все введенные нами предикатные операции бинарны.
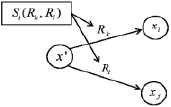
Графически, за счет применения предикатных операций, логическая сеть из плоской становится объемной (рис. 1, а). Такая конструкция имеет физический смысл, т.к. отражает реальное разделение процедур процесса на элементарные базовые действия и операции над этими процедурами. Полученная модификация логической сети является естественной адаптацией ее структуры для рассматриваемой предметной области – построения гибкой процессной модели.
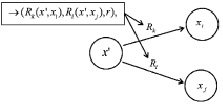
Пример работы логической сети с предикатной операцией последовательного выполнения представлен на рис. 1, б. Пусть задана Si(Rk, Rl, 2). В данном случае 2 означает, какое действие должно выполниться первым. Вначале обязательно выполняется Rl, потом Rk.
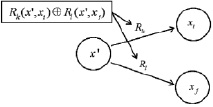
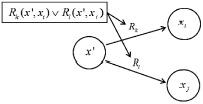
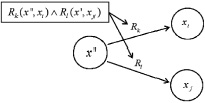
Иллюстрация предикатного представления исключающего и неисключающего выбора, а также параллельного выполнения приведена на рис. 1, в, г, д.
Для операторов последовательного выполнения и цикла важно задать порядок вершин (слева – направо) вне зависимости от их типа, поскольку порядок вершин задает порядок выполнения действий процесса.
В случае цикла одна вершина соответствует началу цикла, содержащему условие повторения (обычно соответствует фрагменту с «do», «for»).
Вершина xj соответствует собственно операции (группе операций) цикла, после которых происходит переход к новому повторению.
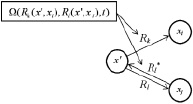
Пример работы логической сети с предикатной операцией цикла
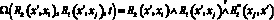
представлен на рис. 1, ж. Пусть задана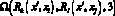 
. Это означает, что вначале должен выполниться 3 раза цикл
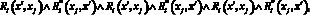
а затем действие Rk(x′, xi).
а б
в
г д
е ж
Рис. 1. Логическая сеть:а – с предикатной операцией; б – последовательное выполнение; в – исключающий выбор; г – неисключающий выбор; д – параллельное выполнение;
е – последовательное выполнение; ж – цикл. В целом модель процесса представляется в виде двухъярусной конструкции – системы бинарных предикатов и системы предикатных операций.
Исходя из общих представлений о процессе, полная модель процесса обязательно должна иметь одно начальное и одно конечное состояние, а также содержать пути достижения конечного состояния. Математически структура описана в [3, 4, 8].
Разработка и реализация программного обеспечения иерархической модели процесса
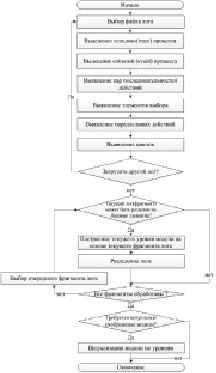
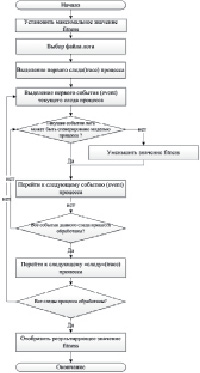
На основе построенной предикатной модели [8] разработано программное обеспечение для визуализации иерархической модели процесса. Предлагаемый в работе алгоритм предназначен для построения модели гибкого процесса, в основе которой лежит дерево процесса. Использование иерархической модели позволяет выделить отдельные ветви, основанные на элементе выбора, и, таким образом, обеспечить возможность отсечения различных вариантов процесса. Разработанный алгоритм в общем виде приведен на рис. 2, а. Алгоритм решения задачи оценки возможности объяснения последовательности событий в логе 2, б.
Пользователю предоставляется исходная форма приложения. Далее Пользователь, пользуясь стандартными функциями, может выбрать и открыть файл с исходными данными.
После открытия файла изменятся статусная строка, отображающая данные, количество узлов и трасс. После этого выполняется дополнительный анализ исходных данных (пункт Analyzing и подпункт Start). Результаты анализа отображаются после выбора подпункта Show. Результаты анализа представлены на рис. 3.
Результаты анализа логов по продуктам и исполнителям позволяют сформировать представленную на рис. 3 в иерархическую структуру.
В данной структуре выделены группы следов процесса, относящиеся к обработке отдельных продуктов, а также имена выполняющих эти процессы работников. Такой подход позволяет детализировать процесс с учетом особенностей предметной области и избежать избыточного обобщения процессов и построения «спагетти – модели».
Для отобранного подмножества следов процесса теперь может быть построена по отдельным уровням модель процесса (рис. 3).
Таким образом, представленный подход позволяет выделить фрагменты процесса с учетом ограничений, сформированных на основе дополнительных атрибутов.
а б
Рис. 2. Алгоритм:
а – формирования модели процесса; б – решения задачи оценки возможности объяснения последовательности событий в логе
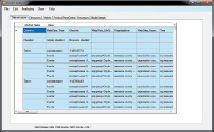
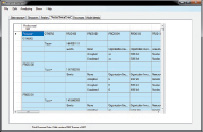
а б
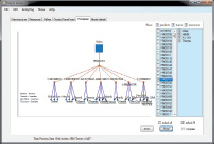
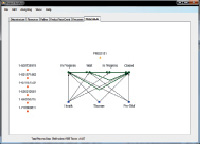
в г
Рис. 3. Пользовательский интерфейс:
а – структура данных; б – разбиение следов процесса по выпускаемым продуктам; в – визуализация ограничений по продуктам и исполнителям; г – детальный уровень модели выделенного фрагмента процесса, для исполнителей из Швеции.
Это дает возможность рассматривать не только традиционные задачи в данной области, связанные с проверкой соответствия реально выполняющегося процесса и модели, созданной при его проектировании, но и решать ряд практически важных задач.
Обобщая указанный перечень задач, можем утверждать, что при современном состоянии процессного подхода к управлению владельцам процесса важно непрерывно его усовершенствовать, добавляя новые возможности как с учетом требований к результатам (выходу процесса), так и с учетом динамики внешней по отношению к процессу среды. Иными словами, рассмотренная в работе задача построения и адаптации гибких процессов в настоящее время является практически важной.
Ключевым моментом при таком усовершенствовании процессов является учет нескольких его аспектов помимо алгоритма действий. В частности, важно учитывать человеческий фактор (исполнителей). Даже полная формализация последовательности работ процесса без учета поведения исполнителей не дает возможность получить эффективный процесс в условиях изменяющейся внешней среды.
Выделение фрагментов процессов с учетом занятых исполнителей процесса позволяет найти узкие места путем сравнения фрагментов процесса, выполняемых разными исполнителями (в разных организациях, странах) при работе с аналогичным продуктом.
Заключение
В статье предложена модель модифицированной направленной логической сети с предикатными операциями (предикатами второго порядка) следующих типов: AND, OR, XOR, цикл, последовательность. В отличие от известной модели логической сети, представляющей собой систему бинарных предикатов, предложенная модификация имеет двуслойную структуру – к традиционной модели логической сети добавлен уровень предикатных операций. Разработанная модель обеспечивает возможность формализации поведения, а также оценки процессов различной физической природы, которые характеризуются заданной последовательностью действий или событий, фиксирующих выполнение действий. Рассмотрен пример последовательности формирования предикатной модели. Разработанная модель может применяться для интеллектуального анализа процессов. Разработанное программное обеспечение позволяет построить иерархическую структуру процесса с учетом дополнительных атрибутов процесса – выпускаемой продукции и исполнителей. Иерархическое представление модели позволяет отразить процесс на организационную структуру и тем самым выделить и визуализировать в обобщенном виде фрагменты процесса, которые выполняются различными подразделениями организации с учетом выпускаемой продукции. Это дает возможность аналитику сравнить выполняемые работы с должностными обязанностями и на этой основе решить проблему перебрасывания ответственности на другое подразделение, а также найти ответственные за это подразделения.
Работа выполнена при поддержке Гранта Российского фонда фундаментальных исследований № 12-08-00296.
Библиографическая ссылка
Рудометкина М.Н., Чехонадских А.В. РАЗРАБОТКА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ИЕРАРХИЧЕСКОЙ МОДЕЛИ ПРОЦЕССА // Фундаментальные исследования. – 2016. – № 8-1. – С. 59-64;URL: https://fundamental-research.ru/ru/article/view?id=40536 (дата обращения: 19.04.2024).