Одним из резервов повышения точности систем автоматического управления является компенсация случайности их физических параметров, причиной которой является воздействие ряда случайных факторов, имеющих место в реальных условиях эксплуатации. Задача компенсации влияния случайности параметров системы на точность и качество ее работы может рассматриваться в двух аспектах. Если речь идет о пассивной компенсации, то данная задача понимается в смысле определения оптимальных значений контролируемых параметров системы управления, например параметров регулятора, обеспечивающих минимизацию влияния случайности других параметров, например параметров объекта управления, которые часто являются неконтролируемыми и изменяющимися под действием разного рода внешних и внутренних случайных факторов. Активная компенсация, с одним из подходов к которой можно познакомиться в статье [5], понимается в смысле формирования такого входного сигнала, который минимизирует влияние случайности параметров системы управления на ее выходной сигнал.
Известно, что случайность параметров системы может оказывать существенное влияние на качество управления в статистическом смысле, например приводить к незапланированному изменению среднего значения выходного сигнала и увеличению его дисперсии, что в конечном итоге ухудшает точность работы системы. Указанные эффекты в целом характерны для стохастических систем, к которым может быть отнесено большинство реальных технических систем. Таким образом, вне зависимости от формулировки, решение задачи компенсации случайности параметров позволяет повысить точность работы системы управления и в этом контексте представляется актуальной проблемой.
Целью настоящей работы является развитие идеи пассивной компенсации в приложении к задаче оптимизации параметров регулятора в контуре управления объектом со случайными параметрами. Как и в работе [5], используется усредненная проекционная модель стохастической системы, построенная с применением методов теории матричных операторов [3]. Пример использования усредненной проекционной модели при решении задачи параметрической идентификации стохастических систем можно найти в статьях [1, 2, 4], а также при решении задачи активной компенсации в вышеупомянутой статье [5]. Данную модель отличает возможность построения эффективных вычислительных алгоритмов. Методы и алгоритмы, построенные на основе проекционной аппроксимации исходной непрерывной математической модели, представленной в виде системы дифференциальных уравнений, принято называть проекционными или спектральными [10]. В последние годы проекционные методы были успешно применены к широкому классу систем, включая стохастические [6, 7, 9], и настоящая статья также может рассматриваться как развитие приложений проекционных методов к задачам теории управления.
Постановка задачи оптимизации параметров регуляторов
Систему с регулятором в контуре управления будем описывать обобщенной математической моделью «вход-выход» в виде линейного дифференциального уравнения
, 
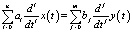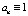, (1)
где все или некоторые коэффициенты ai, bj являются случайными величинами, определяемыми как
, 
;
, 
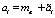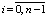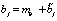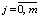, (2)
где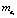 
, 
– математические ожидания,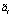 
, 
– центрированные случайные величины. Начальные условия полагаются нулевыми. Условие физической реализуемости системы (1) формулируется как n ≥ m.
В общем случае полагаем, что входной сигнал y(t) – гауссов случайный процесс, для которого задано математическое ожидание my(t) и корреляционная функция Ryy(t1, t2). В распространенном на практике частном случае входной сигнал y(t) является детерминированным, но выходной сигнал x(t) при этом все равно будет случайным. Определяя статистические характеристики сигнала x(t), условимся оставаться в рамках корреляционной теории, то есть полагать, что он, как и процесс y(t), полностью определяется математическим ожиданием mx(t) и корреляционной функцией Rxx(t1, t2). Такую оговорку следует сделать по той причине, что стохастическая система в силу своей природы, искажает нормальный закон распределения случайного процесса y(t). Однако степень этого искажения на практике может быть признана незначительной в силу известного эффекта нормализации случайного процесса инерционной динамической системой. Еще одна причина учитывать только первые два стохастических момента процесса x(t) состоит в том, что в практике инженерных расчетов обычно ограничиваются средним значением и дисперсией, либо среднеквадратическим отклонением.
Математическая модель (1) может быть получена из передаточной функции, которая является конечным результатом стандартных структурных преобразований (сворачивания) структурной схемы системы управления, построенной на основе системы дифференциальных уравнений ее исходной модели. Поскольку ставится задача компенсации случайности физических параметров некоторой реальной системы управления, следует учитывать возможную статистическую связь между коэффициентами уравнения (1), обусловленную тем, что от одного физического случайного параметра (коэффициента одного из уравнений исходной модели) может зависеть более одного коэффициента обобщенной модели (1).
Присутствие регулятора выражается в том, что все или некоторые коэффициенты ai, bj в (1) зависят не только от случайных физических параметров элементов системы управления, но от параметров регулятора, которые будем полагать детерминированными. С целью упрощения мы не показываем явно эту зависимость в модели (1), подразумевая при этом, что указанные коэффициенты зависят от вектора параметров регулятора p = (p1, p2, …), то есть в действительности определяются как ai(p), bj(p). При этом, например, для ПИД-регулятора вектор p будет состоять из трех элементов: p1 = kП, p2 = kИ, p3 = kД.
Требуется найти такие значения параметров регулятора (элементов вектора p), которые обеспечивают минимум отличий статистических характеристик сигнала x(t) от статистических характеристик выходного сигнала эквивалентной детерминированной системы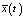 
, также описываемой уравнением (1), где все случайные коэффициенты заменены своими математическими ожиданиями. Следует отметить, что имеется в виду тот относительный минимум отличий, который в принципе может быть достигнут оптимизацией параметров конкретного типа регулятора.
Алгоритм оптимизации параметров регуляторов
Оптимальные значения параметров регуляторов предлагается искать в два этапа. На первом этапе решается задача определения значений параметров регулятора для эквивалентной детерминированной системы. Данная задача может решаться любым из известных методов параметрического синтеза регуляторов детерминированных систем. Например, известен проекционный метод синтеза регуляторов, основанный на минимизации функционала, построенного с использованием проекционной модели системы. Данный функционал имеет следующий вид:
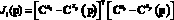, (3)
где 
– проекционная характеристика эталонного переходного процесса xэ(t);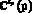 
– расчетная проекционная характеристика переходного процесса 
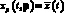, вычисленная по проекционной модели эквивалентной детерминированной системы для некоторых значений параметров регулятора (элементов вектора p); T – знак транспонирования.
Проекционные характеристики функций xэ(t) и xp(t, p) представляют собой вектор-столбцы коэффициентов разложения данных функций по некоторому ортогональному базису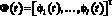 
. Связь между приближенными представлениями указанных функций и их проекционными характеристиками для базиса размерности l определяется как
,
.
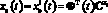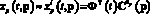Проекционная модель системы с регулятором, используемая при вычислении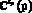 
, является результатом проекционной аппроксимации модели эквивалентной детерминированной системы, выполняемой с применением техники матричных операторов [3]. Данная проекционная модель имеет следующий вид:
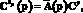, (4)
где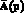 
– матричный оператор эквивалентной детерминированной системы, вычисляемый с использованием матричного оператора интегрирования и, если коэффициенты уравнения (1) зависят не только от параметров p, но от времени, матричного оператора умножения, построенных для базиса Ф(t) [3].
Значения параметров регулятора определяются в результате минимизации функционала (3), то есть вектор параметров регулятора эквивалентной детерминированной системы определяется как
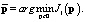
Минимизация функционала J1(p) может быть выполнена одним из известных методов прямого поиска экстремума с проверкой на каждой итерации устойчивости системы и соответствия качества ее переходного процесса некоторым выбранным критериям. Эти условия имеют вид ограничений, определяющих допустимые значения параметров регулятора. При этом может потребоваться введение дополнительных ограничений, связанных с конструктивными особенностями конкретного типа регулятора. Выбор вектора начальных значений параметров регулятора p0 зависит от типа регулятора. Например, для ПИД-регулятора в качестве начальных значений целесообразно выбрать kП = 1, kИ = 0, kД = 0, что фактически соответствует отсутствию регулятора.
На втором этапе выполняется повторная оптимизация параметров регулятора с учетом влияния случайности параметров системы путем минимизации функционала, выражающего меру отличия проекционных характеристик математического ожидания и корреляционной функции выходного сигнала стохастической системы x(t) от тех же проекционных характеристик выходного сигнала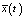 
эквивалентной детерминированной системы с параметрами регулятора 
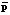, найденными на первом этапе. Данный функционал имеет следующий вид:
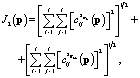(5)
где 
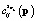и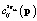 
– элементы квадратных матриц 
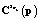и 
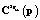, определяемых соответственно как
,
,
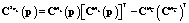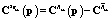где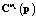 
– проекционная характеристика математического ожидания выходного сигнала стохастической системы; 
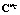– проекционная характеристика математического ожидания выходного сигнала эквивалентной детерминированной системы с параметрами регулятора 
; 
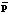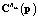– проекционная характеристика корреляционной функции выходного сигнала стохастической системы; 
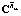– проекционная характеристика корреляционной функции выходного сигнала эквивалентной детерминированной системы с параметрами регулятора 
.
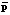Связь между приближенными представлениями математических ожиданий и корреляционных функций выходного сигнала и их проекционными характеристиками для базиса размерности l определяется как
,
,
.
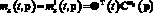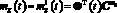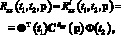
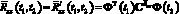При вычислени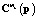и 
и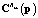 
используется усредненная проекционная модель [4]. Данная модель определяет явную аналитическую зависимость проекционных характеристик математического ожидания и корреляционной функции выходного сигнала стохастической системы от тех же характеристик ее входного сигнала, а также от математических ожиданий и дисперсий, либо корреляционных функций ее случайных параметров, если они являются случайными процессами. В последнем случае случайные коэффициенты модели (1) также будут случайными процессами. Чтобы привести такую модель к виду, подобному (1), то есть к модели с коэффициентами в виде случайных величин, можно представить эти случайные процессы в виде линейной комбинации независимых случайных величин 
, 
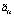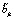, являющихся коэффициентами канонического разложения соответствующих случайных процессов по системам неслучайных координатных функций 
, 
:
, 
;
, 
.
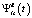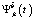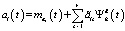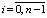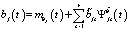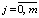Случайные величины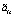 
, 
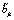имеют нулевые математические ожидания и дисперсии, равные единице. В [9] описан алгоритм вычисления координатных функций, основанный на проекционной аппроксимации корреляционной функции случайного процесса и алгоритме ортогонализации на основе разложения Холецкого. При проекционной аппроксимации такой модели потребуется ранее упомянутый матричный оператор умножения, необходимый для проекционной аппроксимации координатных функций 
, 
.
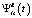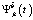Значения параметров регулятора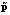 
, учитывающие фактор случайности параметров системы, определяются в результате минимизации функционала (5), то есть
.
Минимизация функционала J2(p) также выполняется методом прямого поиска при тех же ограничениях, что были оговорены для функционала J1(p), но в качестве вектора начальных значений параметров регулятора (начальной точки поиска) используется вектор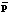 
, найденный на первом этапе оптимизации, то есть 
.
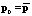Таким образом, второй этап оптимизации параметров регулятора позволяет минимизировать отклонение поведения системы в статистическом смысле от поведения ее детерминированного эквивалента путем соответствующей коррекции значений параметров регулятора, определенных на первом этапе.
Пример оптимизации параметров ПИД-регулятора
Рассмотрим электрогидравлический следящий привод (ЭГСП) с ПИД-регулятором. На вход ПИД-регулятора поступает сигнал ошибки, формируемый блоком сравнения входного сигнала ЭГСП (сигнал y(t) – электрическое напряжение) с сигналом обратной связи. Сигнал с выхода регулятора поступает на вход электромеханического преобразователя первого каскада усиления на основе гидроусилителя типа сопло-заслонка. Второй каскад образован золотниковым гидрораспределителем, управляемым перепадом давления на торцах золотника, который осуществляет переключение потока жидкости между полостями гидроцилиндра. Выходным сигналом ЭГСП является перемещение штока гидроцилиндра (сигнал x(t)), которое измеряется датчиком линейного перемещения, формирующим сигнал обратной связи. Сервопривод такого типа является достаточно типичным, и подробное описание его математической модели можно найти, например, в [8]. Он обладает высокой удельной мощностью и быстродействием, но при этом чувствителен к свойствам рабочей жидкости, температуре окружающей среды и другим факторам, носящим в основном случайный характер.
Рассмотренный выше алгоритм позволяет минимизировать влияние указанных факторов за счет дополнительной оптимизации параметров ПИД-регулятора с учетом возможной случайности некоторых физических параметров ЭГСП. В качестве случайного физического параметра, сильно влияющего на характеристики ЭГСП, будем рассматривать коэффициент сжатия рабочей жидкости kсж(t), который зависит от процента содержания растворенного газа или его пузырьков и может быстро изменяться на интервале исследования, поэтому должен рассматриваться как случайный процесс.
Линеаризованную модель ЭГСП с ПИД-регулятором можно представить в виде следующего дифференциального уравнения:
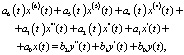
где коэффициенты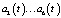 
зависят от указанного случайного параметра, а значит, также являются случайными процессами и, как было отмечено выше, могут быть представлены в виде канонических разложений. Статистические характеристики этих процессов (математические ожидания и корреляционные функции) определяются через те же характеристики физического случайного параметра, которые считаются известными. Иначе они могут быть определены с помощью алгоритма идентификации [1, 2, 4], который также основан на использовании усредненных проекционных моделей стохастических систем.
Чтобы продемонстрировать возможности двухэтапного алгоритма оптимизации параметров регуляторов на самом общем примере, предположим, что входной сигнал ЭГСП также является гауссовым случайным процессом с заданными статистическими характеристиками. На практике такая ситуация имеет место, например, при использовании ЭГСП в качестве силового привода виброиспытательного стенда. При этом требуется воспроизвести случайный испытательный сигнал с минимальными искажениями его статистических характеристик.
Задача оптимизации параметров регулятора формулируется следующим образом. Требуется найти оптимальные параметры ПИД-регулятора kП, kИ, kД, обеспечивающие желаемые динамические характеристики ЭГСП с учетом случайности коэффициента сжатия рабочей жидкости kсж(t). Желаемые динамические характеристики задаются функцией эталонного переходного процесса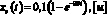 
, который должен иметь место при подаче на вход ЭГСП ступенчатого сигнала 
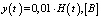. Так как входной сигнал в рассматриваемом примере принят случайным, то 
и 
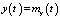. Корреляционная функция входного сигнала 
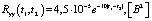, и он полагается гауссовым процессом. Случайный параметр kсж(t) также полагается гауссовым процессом с постоянным математическим ожиданием 
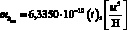и корреляционной функцией
.
Стационарность вышеупомянутых случайных процессов в принципе не является обязательным условием, но принята здесь для упрощения интерпретации результатов. В качестве ортогонального базиса Ф(t) используется базис функций Уолша с l = 64.
На первом этапе искались значения kП, kИ, kД без учета случайности физического параметра ЭГСП (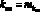
) путем минимизации функционала (3) методом Нелдера – Мида при начальных значениях kП = 1, kИ = 0, kД = 0. В результате были найдены следующие значения: kП = 69,5929, kИ = 4,8419, kД = 1,8544.
На втором этапе искались значения kП, kИ, kД с учетом случайности физического параметра kсж(t) путем минимизации функционала (5) тем же методом при начальных значениях kП = 69,5929, kИ = 4,8419, kД = 1,8544, найденных на первом этапе. В результате были найдены следующие значения: kП = 40,4284, kИ = 0,0042, kД = 4,1849.
Результаты оптимизации параметров ПИД-регулятора представлены на рис. 1 и рис. 2.
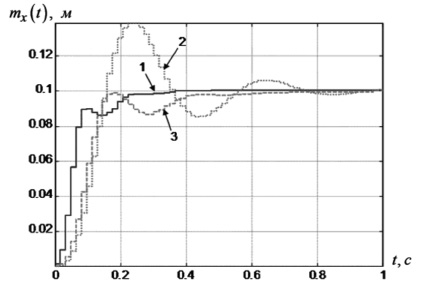
Рис. 1. Математическое ожидание выходного сигнала ЭГСП: 1 – для детерминированной модели после первого этапа оптимизации; 2 – для стохастической модели после первого этапа оптимизации; 3 – для стохастической модели после второго этапа оптимизации
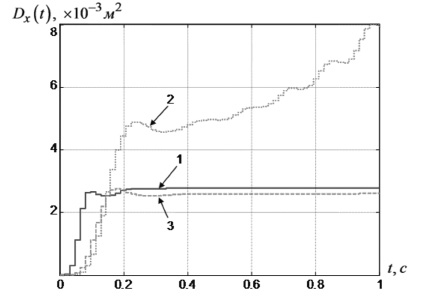
Рис. 2. Дисперсия выходного сигнала ЭГСП: 1 – для детерминированной модели после первого этапа оптимизации; 2 – для стохастической модели после первого этапа оптимизации; 3 – для стохастической модели после второго этапа оптимизации
Из графика рис. 1 видно, что на втором этапе оптимизации удалось значительно улучшить качество переходного процесса по математическому ожиданию (кривая 3 по сравнению с кривой 2), приблизив его к переходному процессу эквивалентной детерминированной системы (кривая 1). Кроме того, график рис. 2 демонстрирует эффект существенного уменьшения дисперсии переходного процесса в установившемся режиме (кривая 3 по сравнению с кривой 2). Видно, что дисперсия выходного сигнала приближается к дисперсии выходного сигнала эквивалентной детерминированной системы (кривая 1).
Вычисления выполнялись на персональном компьютере со следующими техническими характеристиками: CPU Intel Core 2 6600 @ 2.40GHz, RAM 3.0 GB. Программа оптимизации выполнялась в системе MATLAB® (The MathWorks Inc.) версии 7.5.0.342 (R2007b). Для минимизации функционалов (3) и (5) использовалась стандартная функция fmiinsearch с параметрами оптимизации, заданными по умолчанию. Время вычислений для первого этапа алгоритма оптимизации составило примерно 10 с, для второго – около 20 с.
Заключение
Использование усредненных проекционных моделей стохастических систем позволило предложить эффективный алгоритм оптимизации параметров регуляторов систем управления, обеспечивающий минимизацию влияния случайности физических параметров системы на статистические характеристики ее выходного сигнала. Оптимальные значения параметров регулятора определяются путем минимизации функционала, выражающего меру отличия проекционных характеристик математического ожидания и корреляционной функции выходного сигнала стохастической системы от тех же проекционных характеристик выходного сигнала эквивалентной детерминированной системы. Усредненная проекционная модель обеспечивает быстрое вычисление данного функционала при использовании методов прямого поиска минимума, требующих его повторного вычисления на множестве шагов. Дополнительным преимуществом данной модели является отсутствие искусственных ограничений на степень вариации и закон распределения случайных параметров, что позволяет включить в рассмотрение стохастические системы с негауссовыми случайными параметрами, а также высокий потенциал распараллеливания операций.
На примере оптимизации параметров ПИД-регулятора электрогидравлического следящего привода показано, что можно заметно улучшить точность воспроизведения случайного входного сигнала, скомпенсировав влияние случайности одного из физических параметров привода на статистические характеристики его выходного сигнала.
Предлагаемый подход к пассивной компенсации нежелательного влияния случайности физических параметров систем управления на точность и качество их работы представляется простым и экономичным, так как не требует добавления в систему новых элементов, позволяя тем самым избежать усложнения и, соответственно, удорожания технического решения данной проблемы.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (проект № 16-41-400701).
Библиографическая ссылка
Тин Эй Чжо, Макаренков А.М., Тун Тун Чжо, Широкова З.Г. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ РЕГУЛЯТОРОВ СТОХАСТИЧЕСКИХ СИСТЕМ // Фундаментальные исследования. – 2017. – № 4-1. – С. 70-76;URL: https://fundamental-research.ru/ru/article/view?id=41437 (дата обращения: 19.04.2024).