Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Клеванский Н.Н. 1 Антипов М.А. 1 Слепцова Л.А. 1 Романова И.В. 1

---

1 ФГБОУ ВО «Саратовский государственный аграрный университет имени Н.И. Вавилова»

В статье представлены основные концепции и подходы в реализации задач транспортных расписаний на базе двух схем генерации расписаний. Получение начального расписания по первой схеме с использованием критерия наилучшего распределения ресурсов является базовым для второй схемы – этапа оптимизации. Каждая схема включает два правила приоритетов – эвристические процедуры получения решений на базе идеологии жадных алгоритмов, использующих многокритериальное ранжирование. Предложены основные критерии для правил приоритетов в формировании и оптимизации транспортных расписаний – критерии загруженности и равномерности. Во второй схеме критерий равномерности представлен среднеквадратичным отклонением от среднего интервала между событиями расписаний станций и перегонов. Представлены формализованные процедуры многовекторного ранжирования для всех правил приоритетов. Процедура транспортного планирования использует двухэтапный алгоритм, реализованный в среде СУБД.

Статья в формате PDF

0 KB

расписание

заявка

событие

транспортное расписание

жадный алгоритм

правила приоритетов

схема генерации расписаний

среднеквадратичное отклонение

методы ранжирования

1. Клеванский Н.Н., Антипов М.А. Формирование транспортных расписаний // Образовательные ресурсы и технологии. – 2016. – № 4 (16). – С. 71–91.

2. Клеванский Н.Н., Антипов М.А. Формирование начальных расписаний для векторов заявок // Современные наукоемкие технологии. – 2016. – № 10–1. – С. 79–85.

3. Клеванский Н.Н., Антипов М.А. Оптимизация начальных транспортных расписаний // Современные наукоемкие технологии. – 2016. – № 11–2. – С. 264–269.

4. Лазарев А.А., Мусатова Е.Г., Гафаров Е.Р., Кварацхелия А.Г. Теория расписаний. Задачи управления транспортными системами. – М., Физический факультет МГУ, 2012. – 159 с.

5. Сафронов В.В. Основы системного анализа: методы многовекторной оптимизации и многовекторного ранжирования: монография. – Саратов: Научная книга, 2009. – 329 с.

6. Browning T.R., Yassine A.A. Resource-Constrained Multi-Project Scheduling: Priority Rule Performance Revisited // International Journal of Production Economics. – 2010. – № 126 (2). – Р. 212–228.

7. Burdett R. and E. Kozan. A sequencing approach for creating new train timetables // OR Spectrum. – 2010. – № 32 (1). – Р. 163–193.

8. Cacchiani V., Toth P. Nominal and Robust Train Timetabling Problems // European Journal of Operational Research. – 2012. – № 219(3). – Р. 727–737.

9. Hansen I.A., Pachl J. (eds.): Railway Timetabling & Operations. Analysis – Modelling – Optimisation – Simulation – Performance Evaluation. 2nd edition. Eurailpress. – 2014. – 332 p.

10. Harrod S.S. A tutorial on fundamental model structures for railway timetable optimization // Surveys in Operations Research and Management Science. – 2012. – № 17 (2). – Р. 85–96.

Управление транспортными системами включает иерархически взаимосвязанные проблемы стратегического, тактического и оперативного уровней [4, 9]. Многие проблемы транспортных систем решаются на тактическом уровне [4] в зависимости от расписания регулярного пассажирского транспорта. «Сложность решения задач маршрутизации и формирования расписания определяется жесткостью ограничений на пропускную способность путей и транспортные средства. Одним из представителей транспортных систем с достаточно жесткими ограничениями является железнодорожный транспорт с постоянным сезонным расписанием пассажирских поездов» [4].

Задача формирования железнодорожных расписаний в европейских публикациях рассматривается в двух видах: цикличном и нецикличном [8]. Цикличные расписания строго периодичны в пределах суток или части суток, тогда как нецикличные расписания, являющиеся также периодическими, имеют период равный суткам или нескольким суткам. Для формирования и оптимизации железнодорожных расписаний (NP-трудных задач) используются различные подходы, прежде всего в форме эвристик [7–10]. В мультипроектном планировании [6] основой эвристических подходов является использование схем формирования расписаний (SGS – schedule generation scheme) и правил приоритетов (PR – priority rules). Приоритетами в этом контексте выступают критерии для определения очередности конкурирующих по ресурсам работ/проектов. Критерии являются скалярными величинами разных характеристик заявок/работ и проектов, включая выделяемые и требуемые ресурсы. Под правилами приоритетов понимаются задаваемые последовательности приемов и методов определения очередности. Основой правил приоритетов является однокритериальное ранжирование скалярных величин приоритетов. В исследованиях по формированию железнодорожных расписаний подобных подходов не обнаружено.

Целью статьи является представление схем генерации транспортных расписаний и правил приоритетов на основе методов ранжирования в программном формировании расписания движения пассажирского железнодорожного транспорта дальнего следования.

Исследование систем различного рода использует критерии с векторными и многовекторными компонентами. Задачи принятия решений в этом случае сводятся к задачам многокритериального, многовекторного и гипервекторного ранжирования [5].

Для однозначного понимания терминологии введем следующие определения:

- многокритериальным ранжированием является ранжирование критериев – упорядоченных множеств скалярных компонент. Наиболее адекватным многокритериальным ранжированием является «жесткое» ранжирование [5]. Будут различаться прямое (по «возрастанию») и обратное (по «убыванию») многокритериальное ранжирование;

- многовекторным ранжированием является ранжирование критериев – упорядоченных множеств векторных компонент. Многовекторное ранжирование n критериев с k векторными компонентами осуществляется следующим образом: k «жестких» ранжирований соответствующих векторных компонент с формированием рангов; «жесткое» ранжирование n векторов рангов;

- гипервекторное ранжирование – ранжирование критериев – упорядоченных множеств многовекторных компонент. Гипервекторное ранжирование m критериев, которые содержат n многовекторных критериев с k векторными компонентами, осуществляется следующим образом: k «жестких» ранжирований соответствующих векторных компонент с формированием рангов; n «жестких» ранжирований соответствующих векторов рангов многовекторных компонент с формированием рангов; «жесткое» ранжирование m векторов рангов гипервекторных компонент.

Для расчета расписания движения пассажирского железнодорожного транспорта дальнего следования предложены две последовательно применяемые схемы генерации расписаний: SGS1 – формирование начального расписания; SGS2 – последующая оптимизация [1].

В каждом цикле SGS1 используются два взаимосвязанных правила приоритетов PR11 и PR12. Стратегия PR11 связана с выбором наиболее загруженного по требуемым ресурсам железнодорожной сети маршрута среди маршрутов, не включенных в начальное расписание. Для маршрута, выбранного правилом PR11, в правиле PR12 определяется время отправления с начальной станции с обеспечением наибольшей равномерности потребления ресурсов сети.

В каждом цикле SGS2 также используются два взаимосвязанных правила приоритетов PR21 и PR22. Стратегия PR21 связана с выбором маршрута, наиболее неравномерного по потреблению ресурсов сети в существующем расписании. Для маршрута, выбранного правилом PR21, в правиле PR22 определяется время отправления с начальной станции, по крайней мере не ухудшающее показатели равномерности всего расписания.

Рассмотрим применение схем SGS1, SGS2 и правил приоритетов PR11, PR12, PR21 и PR22.

В начале каждого цикла формирования начального расписания (схема SGS1) осуществляется перерасчет оценок загруженности станций и перегонов сети [2].

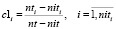, (1)

где nti – количество поездов, проходящих через i-ую станцию;

niti – количество поездов начального расписания, проходящих через i-ую станцию;

nt – количество поездов в интервале расписания;

nit – количество включенных в начальное расписание поездов.

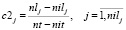, (2)

где nlj – количество поездов, проходящих через j-ый перегон;

nilj – количество поездов начального расписания, проходящих через j-ый перегон.

Оценки загруженности станций (1) и перегонов (2) формируют множества первых и вторых векторных компонент критериев загруженности маршрутов

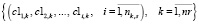; (3)

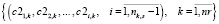, (4)

где nr – количество не включенных в начальное расписание маршрутов;

nk,s – количество станций маршрута rk.

Скалярная оценка загруженности k-го маршрута по суткам расписания

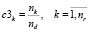, (5)

где nk – количество суток отправления поездов k-ого маршрута;

nd – количество суток интервала расписания;

nr – количество маршрутов железнодорожной сети.

Критерии загруженности маршрутов включают две векторные компоненты и одну скалярную. Для определения самого загруженного маршрута в правиле PR11 применяется многовекторное ранжирование, заключающееся в следующем.

Многокритериальным ранжированием векторов (3) и (4) формируются множества рангов маршрутов по загруженности станций и перегонов

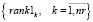; (6)

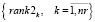. (7)

Обратная сортировка выражений (5) порождает множество рангов маршрутов по загруженности суток интервала расписания

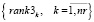. (8)

Ранги (6, 7, 8) формируют множество векторов рангов маршрутов

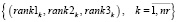. (9)

Старший по рангу маршрут, полученный многокритериальным ранжированием векторов (9), является самым загруженным и его следует включить в начальное расписание. Для этого согласно схеме SGS1 необходимо определение оценок равномерности расписаний перегонов и станций [2].

Оценки равномерности событий расписания i-ой станции определяются как

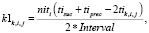
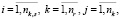(10)

где tiprec и tisuc – времена прибытия на i-ую станцию поездов, предшествующих и последующих по отношению ко времени tik,i,j в интервале расписания.

Оценки равномерности распределения событий в периодах расписания i-ой станции

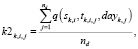
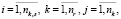(11)

где

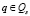 – множество булевых обозначений событий станций.

Оценки равномерности событий расписания i-ого перегона определяются как

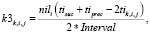
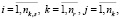(12)

где tiprec и tisuc – времена начала движения поездов на i-ом перегоне, предшествующих и последующих по отношению ко времени tik,i,j.

Оценки равномерности распределения событий в периодах расписания i-ого перегона на въезде/выезде со станции

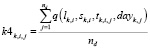, (13)

где

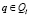 – множество булевых обозначений событий перегона.

Согласно схеме SGS1 осуществляется цикличное накопление множеств векторов значений оценок равномерности (10–13) расписаний перегонов и станций с учетом обязательных ограничений в интервале от 0 до 24 часов с шагом 0,1 часа в пределах суток отправления поездов выбранного правилом PR11 маршрута. Каждый вектор идентифицируется временем цикла tini+1,1 – временем отправления поездов выбранного маршрута с начальной станции, ni – количество маршрутов, включенных в начальное расписание. В состав векторов включаются оценки равномерности станций и перегонов выбранного маршрута, так как изменений этих оценок для других станций и перегонов не будет.

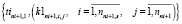, (14)

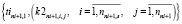, (15)

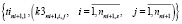, (16)

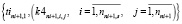. (17)

Векторы (14–17) определяют критерии равномерности начального расписания для каждого tini+1,1. Для нахождения tini+1,1, обеспечивающего наибольшую равномерность начального расписания при включении в него поездов выбранного маршрута, правило PR12 должно реализовать многовекторное ранжирование критериев равномерности (14–17).

Многокритериальные ранжирования векторов каждого множества (14–17) формируют множества векторов рангов для начальных времен движения поездов маршрута.

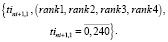(18)

Многокритериальное ранжирование векторов (18) определяет начальное время отправления поездов выбранного маршрута в начальном расписании. Включением последнего маршрута в начальное расписание работа схемы генерации SGS1 завершается.

Оптимизация начального расписания по схеме SGS2 использует интегральные оценки равномерности расписаний станций и перегонов в виде среднеквадратичных отклонений [3].

Оценка равномерности распределения событий i-ой станции в интервале расписания

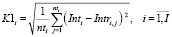, (19)

где 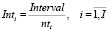 – среднее значение интервала между прибытиями поездов на i-ую станцию;

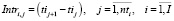 – величина интервала между прибытиями на станцию двух ближайших по времени поездов. Для .

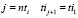Оценка равномерности распределения событий i-ого перегона в интервале расписания

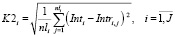, (20)

где 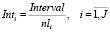 – среднее значение интервала между началами движения поездов по i-ому перегону;

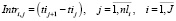 – величина интервала между началами движения поездов по i-ому перегону двух ближайших по времени поездов. Для .

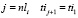В начале каждого цикла схемы SGS2 осуществляется расчет оценок равномерности распределения событий станций (19) и перегонов (20) в интервале расписания сети, формирующий множества векторных компонент критериев равномерности маршрутов

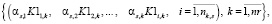(21)

где αs,i – коэффициент важности оценки, ;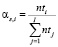

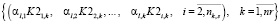, (22)

где αl,i – коэффициент важности оценки, .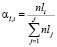

.

Критерии равномерности маршрутов включают две векторные компоненты, а для определения самого неравномерного маршрута в правиле PR21 используется многовекторное ранжирование, заключающееся в следующем.

Раздельное многокритериальное ранжирование векторов (21) и (22) формирует множества рангов маршрутов по равномерности расписаний станций (23) и перегонов (24)

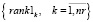, (23)

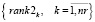. (24)

Это позволяет сформировать множество векторов рангов маршрутов

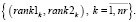(25)

Многокритериальное ранжирование векторов (25) определяет самый неравномерный маршрут при принятых оценках и критериях равномерности. Он становится очередным кандидатом на перестановку в расписании.

Согласно схеме SGS2 осуществляется цикличное накопление множеств векторов значений оценок равномерности (21–22) аналогично схеме SGS1.

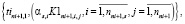(26)

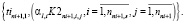(27)

Многокритериальные ранжирования векторов (26, 27) формируют множества векторов рангов для начальных времен движения поездов маршрута

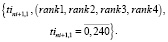(28)

Многокритериальное ранжирование векторов (28) определяет начальное время движения поездов маршрута в оптимизированном расписании железнодорожной сети. Завершение работы SGS2 определяется выбранной стратегией оптимизации – одно- или многопроходной.

Авторы считают, что новыми являются следующие положения и результаты:

● представлены две взаимосвязанные схемы генерации транспортного расписания;

● сформулированы правила приоритетов каждой схемы генерации транспортных расписаний с использованием методов ранжирования теории принятия решений.

Библиографическая ссылка