По мере роста и усложнения промышленных предприятий актуальными становятся проблемы их построения и обеспечения функционирования. Законы развития техники, включающей отдельные элементы, и живой природы, состоящей из отдельных особей, имеют много общего. Поэтому представляется возможным описывать сложные электротехнические системы на основе ценологических понятий.
Известно, что в 1877 г. при исследовании свойств отдельных особей и совокупностей живых организмов Клаус Мебиус ввел понятие «биоценоз». Биоценоз – совокупность живых организмов, обитающих на определенном участке, где условия внешней среды определяют его видовой состав.
Термин «техноценоз» и ценологический подход к исследованию сложных технических систем предложены в 1974 г. замечательным ученым Б. И. Кудриным, где техноценоз определяется как сообщество всех изделий, включающее все популяции; ограниченное в пространстве и времени; имеющее слабые связи и слабые взаимодействия элементов (изделий), образующих систему искусственного происхождения, которая характеризуется несопоставимостью времени жизни ценоза и особи, невозможностью выделения однозначной системы показателей. Устойчивость системы обусловлена действием законов энергетического и информационного отборов по аналогии с живыми системами, где действует закон естественного отбора.
Кудрин Б.И. предложил использовать модель H-распределения для математического описания видового и рангового распределения. Применительно к промышленным предприятиям определяют, например, связь между количеством видов продукции и электропотреблением.
Для рангового распределения показатель b меняется в пределах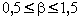 
. На основе зависимости годового электропотребления от разнообразия и структуры выпускаемой продукции прогнозируют параметры электропотребления, опираясь на объем выпускаемой продукции.
Отмеченные ценологические свойства промышленных предприятий констатируют устойчивость явления, проявляющегося с определенного уровня организации некоторого множества элементов с неопределенными связями: способность ценозов формировать в процессе образования и сохранять в процессе развития устойчивую структуру при наличии различных механизмов отбора. Данная теория предполагает существование некоторого идеального распределения элементов ценоза.
Объясним существование идеальной технической системы с точки зрения гармонии и золотого сечения. Предположим, что гармония и идеальное распределение видов ценоза как системы, выполняющей свое функциональное назначение, подчиняются золотому сечению, а понятие золотое сечение неразрывно связано с числами Фибоначчи.
Считается, что деление отрезка в среднем и крайнем отношении впервые было осуществлено 2500 лет назад Пифагором. Он показал, что отрезок единичной длины AB можно разделить точкой С на две части так, что отношение большей части (CB=x) к меньшей (AC=1-x) будет равняться отношению всего отрезка (AB=1) к большей части (CB): CB/AC=(AC+CB)/CB, или x/(1-x)=1/x. Единичный отрезок АВ ( 0,382+0,618=1) делится точкой С в соответствии с пропорцией 1:0,618 = 0,618:0,382 = 1,618. Такое отношение принято называть золотой пропорцией, а соответствующее деление отрезка - золотым делением.
В 1202 г. вышло в свет сочинение "Liber abacci" итальянского купца и математика Леонардо Пизанского (1180-1240 г.г.), известного как Фибоначчи. Он обнаружил последовательность чисел, где последующее число равно сумме двух предыдущих чисел: 1; 1; 2; 3; 5; 8; 13; 21; 34, 55, и т.д., эта последовательность получила название ряда Фибоначчи.
Интерес к золотому сечению сохраняется и в наши дни. В нашу задачу входит показать значение золотого сечения и чисел Фибоначчи в сфере организации электротехнических систем по аналогии с живой природой. Если взять числовой ряд 1,0; 0,62; 0,38; 0,24; 0,15; 0,09 и т.д. (что напоминает шкалу мощностей трансформаторов), состоящий из чисел с коэффициентом 1,618 («Золотое сечение») и аппроксимировать этот ряд, то получим гиперболическую кривую, которая описывается следующей формулой:
где b = 1,63 - ранговый коэффициент
Этим числовым рядом можно описывать при ранжировании в ценозе соотношение количества видов и численности каждого вида.
Библиографическая ссылка
Южанников А. Ю., Попов Ю.П., Южанников М. Ю. Н-МОДЕЛЬ ТЕХНОЦЕНОЗА И ЧИСЛА ФИБОНАЧЧИ // Фундаментальные исследования. – 2007. – № 12-2. – С. 271-272;URL: https://fundamental-research.ru/ru/article/view?id=4165 (дата обращения: 19.04.2024).