Постановка научной задачи
Одной из актуальных задач информационной безопасности является радиоэлектронная защита (РЭЗ) радиоканалов, по которым осуществляется оперативное управление распределенными критически важными объектами. Анализ информационных источников [1–4] показывает, что подавление таких каналов, реализуемых на базе систем транкинговой радиосвязи, возможно за счет аэродинамических передатчиков помех (АПП), создающих широкополосные заградительные помехи. В настоящее время АПП могут быть легко реализованы с помощью беспилотных летательных аппаратов (БЛА) в виде дронов (квадрокоптеров) или парашютируемых передатчиков помех (ПП). Свое предназначение маломощные АПП осуществляют путем их барражирования и зависания в районе постановки помех с включенными на излучение ПП. Предполагается, что для эффективного РЭП транкинговой связи в определенной области пространства будет осуществляться массированное применение АПП, располагаемых в виде эквидистантной решетки относительно подавляемых радиоприемных устройств (РПУ), прежде всего базовых станций [1, 2].
Анализ особенностей в организации транкинговой радиосвязи и во взаимном расположении группировки АПП и подавляемого РПУ показывает, что для РЭЗ возможно использование пространственных различий между углами прихода сигнала и помех, но только по углу возвышения θ, т.е. в вертикальной плоскости (ВП). Следовательно, для решения задачи пространственной селекции помех, создаваемых группировкой АПП, необходимо наличие априорной информации об угловом распределении помехового поля (угловом спектре мощности помех) в вертикальной плоскости в раскрыве приемной антенны.
Научная задача, решаемая в статье, заключается в разработке математической модели пространственно-временной структуры (ПВС) помехового воздействия, создаваемого группировкой АПП, в вертикальной плоскости. Цель работы состоит в получении аналитической зависимости распределения интенсивности мощности помех 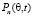 на входе антенны подавляемого РПУ от угла возвышения q для конкретного момента времени t. Поскольку углы прихода помех являются случайными величинами, то модель должна обеспечивать получение статистических характеристик (математического ожидания М и СКО s), т.е.
на входе антенны подавляемого РПУ от угла возвышения q для конкретного момента времени t. Поскольку углы прихода помех являются случайными величинами, то модель должна обеспечивать получение статистических характеристик (математического ожидания М и СКО s), т.е.
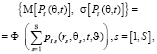 (1)
(1)
где S – количество АПП в группировке, s – номер текущего АПП; 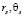 – координаты s-го АПП в виде радиус-вектора и угла возвышения,
– координаты s-го АПП в виде радиус-вектора и угла возвышения, 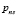 – мощность помехи, создаваемая s-м АПП, на входе подавляемого РПУ; U – совокупность условий, влияющих на распространение помеховых радиоволн.
– мощность помехи, создаваемая s-м АПП, на входе подавляемого РПУ; U – совокупность условий, влияющих на распространение помеховых радиоволн.
Отдельно следует остановиться на особенностях распространения помеховых радиоволн. Применяющиеся на практике транкинговые системы существенно различаются диапазоном рабочих длин волн (l от 0,345 до 2,174 м), поэтому на распространение помеховых радиоволн по-разному будет влиять земная поверхность, т.к. для разных l будет свой тангенс угла потерь в среде распространения [5]. Следовательно, эти обстоятельства должны быть учтены в разрабатываемой математической модели.
Решение научной задачи
Очевидно, что строгое решение волновых дифференциальных уравнений поля помех с учетом граничных эффектов раздела двух сред, а также различных свойств среды распространения и априорной неопределенности координат АПП чрезвычайно затруднено. В этом случае вероятностные характеристики создаваемого помехового воздействия можно получить на основе сочетания статистического подхода к пространственно-временному распределению (ПВР) углов прихода помех, создаваемых АПП в ВП [6, 7], с одной стороны, и феноменологического подхода к задаче определения ПВР помехового поля в точки подавления [8, 9], с другой стороны. Исходя из этого, требуемая модель ПВС разрабатывалась в два этапа:
1) статистическое моделирование ПВР углов прихода помех в ВП;
2) математическое моделирование ПВС помехового воздействия в ВП.
Исходными данными для моделирования выступают технические характеристики современных маломощных ПП, а также тактика группового применения АПП [1–4]. В основу моделирования помехового воздействия положена модель точечных источников влияния [7], которая конкретизирована применительно к АПП. Каждый АПП характеризуется функцией воздействия, имеющей физический смысл мощности помех, приведенной к полосе пропускания РПУ, с учетом характеристики направленности антенны ПП, т.е.
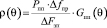 , (1')
, (1')
где 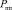 – мощность передатчика помех;
– мощность передатчика помех; 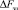 – ширина спектра заградительной помехи;
– ширина спектра заградительной помехи; 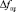 – полоса пропускания РПУ;
– полоса пропускания РПУ; 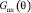 – диаграмма направленности антенны ПП.
– диаграмма направленности антенны ПП.
В результате каждый АПП создает в точке расположения подавляемого РПУ поле воздействия, определяемое как произведение функции воздействия ρ(θ) на передаточную характеристику 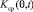 среды распространения.
среды распространения.
В первой статистической части произведено моделирование стохастической взаимосвязи подавляемого РПУ и группировки АПП в виде эквидистантной решетки. Для этого рассмотрим некоторую область U конечного объема в 4-мерном евклидовом пространстве R4, которая является областью физического пространства и времени. В этой области рассеяна в виде эквидистантной решетки счетная система из S АПП, расположенных в точках 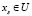 (s = 1, S). Очевидно, что максимальное РЭП наступит в момент времени
(s = 1, S). Очевидно, что максимальное РЭП наступит в момент времени 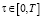 , когда РПУ оказывается в объеме U0, который ограничен расположением четверки ближайших АПП, находящихся в центре решетки. При этом расстояние LT до траверса ближайшего АПП в данный момент времени является случайной величиной, распределенной по равномерному закону с плотностью
, когда РПУ оказывается в объеме U0, который ограничен расположением четверки ближайших АПП, находящихся в центре решетки. При этом расстояние LT до траверса ближайшего АПП в данный момент времени является случайной величиной, распределенной по равномерному закону с плотностью 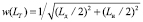 , где Lи – интервал между ПП в ряду решетки, а Lд – дистанция между рядами.
, где Lи – интервал между ПП в ряду решетки, а Lд – дистанция между рядами.
Разбив область U на четыре непересекающиеся области (подрешетки) U1, U2, U3 и U4 относительно центра решетки, с учетом детерминированности взаимного расположения АПП, для конкретной z-й реализации случайных координат 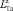 ,
, 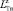 и
и 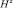 ближайшего АПП относительно местоположения РПУ, получим выражение (2), определяющее расстояние до траверса s-ro АПП в i-й подрешетке, т.е.
ближайшего АПП относительно местоположения РПУ, получим выражение (2), определяющее расстояние до траверса s-ro АПП в i-й подрешетке, т.е.
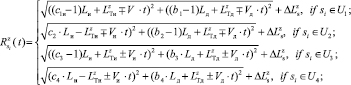 (2)
(2)
где сi и bi (i = 1,4) – соответственно номер ряда в i-й подрешетке и номер АПП в ряду; 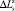 – величина погрешности горизонтальной координаты АПП, обусловленная неточностью их наведения и турбулентностью воздушных потоков; Z – объем выборки реализаций случайного взаимного расположения РПУ и решетки АПП. Величины Vи, Vд представляют собой проекции вектора скорости перемещения АПП в горизонтальной плоскости, они введены в (2) для обеспечения адекватности модели на случай, когда для подавления применяется группировка парашютируемых ПП, либо когда АПП барражируют в районе подавления.
– величина погрешности горизонтальной координаты АПП, обусловленная неточностью их наведения и турбулентностью воздушных потоков; Z – объем выборки реализаций случайного взаимного расположения РПУ и решетки АПП. Величины Vи, Vд представляют собой проекции вектора скорости перемещения АПП в горизонтальной плоскости, они введены в (2) для обеспечения адекватности модели на случай, когда для подавления применяется группировка парашютируемых ПП, либо когда АПП барражируют в районе подавления.
В свою очередь угол прихода помех, определяемый как угол возвышения s-го АПП над горизонтом, равен
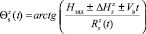 , (3)
, (3)
где Нзад – заданная высота полета АПП, 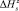 – величина неопределенности вертикальной координаты АПП, а Vв – проекция вектора скорости перемещения АПП на вертикальную ось.
– величина неопределенности вертикальной координаты АПП, а Vв – проекция вектора скорости перемещения АПП на вертикальную ось.
Таким образом, для получения функции распределений 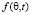 углов прихода помех в конкретный момент времени необходимо методом статистических испытаний разыграть различные варианты взаимного расположении решетки АПП относительно подавляемого РПУ. По результатам накопленной статистики для диапазона углов возвышения
углов прихода помех в конкретный момент времени необходимо методом статистических испытаний разыграть различные варианты взаимного расположении решетки АПП относительно подавляемого РПУ. По результатам накопленной статистики для диапазона углов возвышения 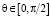 дискретно с шагом Δθ определяется гистограмма распределения углов прихода помех от интервала углов возвышения. При этом среднее значение (математическое ожидание) и СКО функции распределения углов прихода помех определяются следующими выражениями:
дискретно с шагом Δθ определяется гистограмма распределения углов прихода помех от интервала углов возвышения. При этом среднее значение (математическое ожидание) и СКО функции распределения углов прихода помех определяются следующими выражениями:
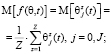 (4)
(4)
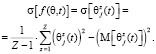 (5)
(5)
В результате моделирования получена асимптотически не смещенная оценка среднего количества радиолучей помехового воздействия от углов прихода, попадающих в интервалы углов возвышения. Таким образом, полученные выражения (4) и (5) представляют собой статистическую модель ПВР углов прихода помех, создаваемых группировкой АПП.
На 2-м этапе моделирования произведено математическое описание структуры помехового поля в ВП с учетом явления интерференции помеховых радиоволн за счет влияния земной поверхности. Поскольку ПВР углов прихода помех в ВП в точке подавления имеет нестационарный и случайный характер, то среда распространения может быть представлена в виде линейного пространственного фильтра (ПФ), у которого передаточная характеристика (ПХ) имеет нестационарный характер, так как зависит от текущего времени воздействия.
Расстояния от АПП до точки подавления (раскрыва антенны РПУ) для прямой 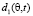 и отраженной
и отраженной 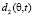 радиоволны связаны с углом возвышения θ соответственно следующими соотношениями:
радиоволны связаны с углом возвышения θ соответственно следующими соотношениями:
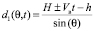 ,
,
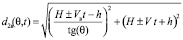 , (6)
, (6)
где H – начальная высота полета АПП, h – высота подъема приемной антенны РПУ. Тогда для прямой волны на расстоянии 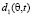 мощность заградительной помехи на входе РПУ, в пределах его полосы пропускания (при условии, что ΔFЗП >> Δfпр) будет равна
мощность заградительной помехи на входе РПУ, в пределах его полосы пропускания (при условии, что ΔFЗП >> Δfпр) будет равна
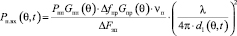 , (7)
, (7)
где 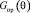 – диаграмма направленности антенны РПУ; vП – коэффициент, учитывающий различия поляризации помехи и сигнала; l – рабочая длина волны радиосигнала.
– диаграмма направленности антенны РПУ; vП – коэффициент, учитывающий различия поляризации помехи и сигнала; l – рабочая длина волны радиосигнала.
Поскольку антенна подавляемого РПУ и АПП находятся высоко над земной поверхностью, то с учетом влияния подстилающей поверхности интерференционный множитель ослабления определяется формулой
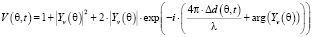 , (8)
, (8)
где 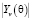 и
и 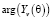 – соответственно модуль и фаза комплексного коэффициента отражения (Френеля) в ВП;
– соответственно модуль и фаза комплексного коэффициента отражения (Френеля) в ВП; 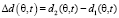 – разность хода лучей прямых и отраженных помеховых радиоволн.
– разность хода лучей прямых и отраженных помеховых радиоволн.
В результате ПХ среды распространения в ВП, как ПФ, будет определяться формулой (9), показывающей, как ослабляется энергия помехи в зависимости от угла ее прихода в ВП:
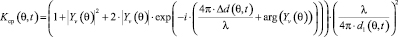 . (9)
. (9)
Полученные в результате моделирования формализованные представления углов прихода помех в виде функции распределения 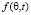 и среды распространения в виде передаточной характеристики
и среды распространения в виде передаточной характеристики 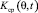 позволяют описать помеховое воздействие в точке приема (на входе антенны) в виде среднестатистического углового спектра мощности помех (УСМП) в ВП в конкретный момент времени t. При этом математическое выражение, описывающее среднее значение УСМП в ВП, в общем виде имеет вид
позволяют описать помеховое воздействие в точке приема (на входе антенны) в виде среднестатистического углового спектра мощности помех (УСМП) в ВП в конкретный момент времени t. При этом математическое выражение, описывающее среднее значение УСМП в ВП, в общем виде имеет вид
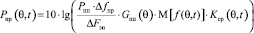 , [дБ],
, [дБ], 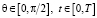 , (10)
, (10)
где Т – время помехового воздействия АПП.
Выражение (10) представляет собой математическую модель, которая в абстрактной форме описывает ПВС помехового воздействия, создаваемого группировкой АПП в виде эквидистантной решетки. Физический смысл УСМП заключается в том, что 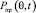 демонстрирует, как в точке подавления распределена интенсивность мощности помех от угла возвышения (прихода помех) в конкретный момент помехового воздействия.
демонстрирует, как в точке подавления распределена интенсивность мощности помех от угла возвышения (прихода помех) в конкретный момент помехового воздействия.
Результаты исследования и их обсуждение
С помощью разработанной модели с доверительной вероятностью 0,95 получено ПВР углов прихода помех в ВП, представляющее собой сглаженные статистические гистограммы. Моделирование производилось для случая массированного подавления РПУ базовой станции решеткой из 64-х АПП, равномерно распределенных в пространстве с интервалом и дистанцией в 500 м и включившихся на излучение на высоте 500 м и плавно снижающихся со скоростью 1–2 м/с. Полученные зависимости среднего значения 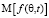 и СКО
и СКО 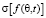 представлены на рис. 1, а, б.
представлены на рис. 1, а, б.
В результате исследований установлено, что ПВР углов прихода помех для конкретного момента времени сводится к устойчивому распределению. В фиксированный момент времени в ПВР имеется три характерных сектора углов возвышения:
1) сектор, в котором помехи отсутствуют, если 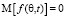 ;
;
2) детерминированный сектор, в котором помехи приходят всегда, если 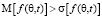 ;
;
3) сектор, в котором помехи появляются спорадически, если 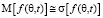 .
.
Данные результаты следует использовать для пространственной селекции помех, создаваемых группировкой АПП.
Из анализа графиков, приведенных на рис. 2, а, б, следует, что ПХ среды распространения в ВП имеет сложный осциллирующий характер, который уменьшается при приближении угла возвышения к углу Брюстера (полного преломления радиоволн). При этом коэффициент передачи плавно возрастает с увеличением угла возвышения, поскольку при этом уменьшается расстояние от точки подавления до места расположения АПП.
Графики УСМП в точке подавления в начальный момент времени, а также через 120 секунд, приведены на рис. 3, а, б. Утолщенными линиями обозначены средние значения УСМП, а тонкими – его максимальные значения в пределах полученной дисперсии. Исследование УСМП показало, что его детерминированная часть вносит основной вклад в интегральную мощность помех и характеризуется наличием характерных экстремумов. Кроме того установлено, что неустойчивость УСМП течение времени t проявляется в сужении сектора, в котором помехи отсутствуют, в снижении углов характерных экстремумов детерминированного сектора и в увеличении спорадического сектора. Полученная в результате моделирования ПВС помехового воздействия в виде УСМП в ВП позволяет сформулировать требования к диаграмме направленности антенной системы подавляемого РПУ.
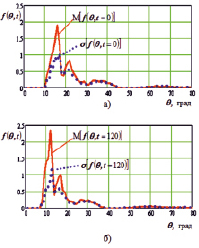
Рис. 1. Пространственно-временное распределение углов прихода помех в ВП
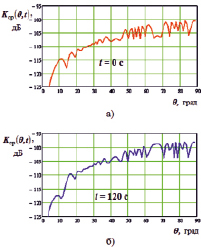
Рис. 2. Передаточная характеристика среды распространения в ВП
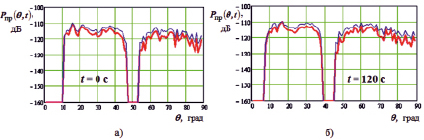
Рис. 3. Угловой спектр мощности помех в ВП
Заключение
В статье разработана математическая модель помехового воздействия в ВП, создаваемого группировкой АПП в виде эквидистантной решетки. Данная модель представляет собой математическое описание ПВС помехи на входе антенны подавляемого РПУ в виде среднестатистического УСМП в ВП для конкретного момента времени. Полученные в результате моделирования априорные данные об УСМП в ВП следует использовать для пространственной селекции помех, создаваемых АПП.
Библиографическая ссылка
Сагдеев К.М., Сагдеева Е.К. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ СТРУКТУРЫ ПОМЕХОВОГО ВОЗДЕЙСТВИЯ ОТ АЭРОДИНАМИЧЕСКИХ ПЕРЕДАТЧИКОВ // Фундаментальные исследования. – 2017. – № 8-2. – С. 308-313;URL: https://fundamental-research.ru/ru/article/view?id=41666 (дата обращения: 26.04.2024).



