Описание эволюции ансамбля выделений в металлических сплавах является исключительно сложной задачей, и ее аналитическое решение возможно только для самых простых случаев. Наиболее общая модель для моделирования эволюции выделений второй фазы в ограниченной матрице для многокомпонентной системы была развита Агреном в работе [1]. Но продолжают развиваться и другие методы прогнозирования поведения выделений второй фазы при термической обработке, основанные на компьютерном моделировании. Например, в работе [2, 3] предлагается подход, основанный на поиске максимума скорости рассеяния энергии Гиббса в системе. Этот подход успешно использовался в ряде работ [4–6] для моделирования эволюции карбонитридных выделений в сталях. В некоторых исследованиях [7, 8] продолжается развиваться так называемая KWN-модель. В [7] она была расширена для учёта зарождения, а в [8] учитывается возможность изменения состава выделений.
Методы для прогнозирования эволюции выделений вторых фаз достаточно давно развиваются и авторами. В недавних работах [9–10] предложенный авторами ранее [11] подход был обобщён на случай многофазных многокомпонентных систем и выполнены расчеты эволюции карбонитридных выделений в сталях без учета возможности образования новых частиц вторых фаз. В настоящей работе была поставлена задача распространить разработанный нами метод на случай многофазных многокомпонентных систем, в которых возможно образование новых зародышевых центров. Кроме того, ставилась задача исследовать возможность распараллеливания данного алгоритма.
Описание модели
При построении модели предполагалось, что все выделения имеют сферическую форму и постоянный состав, на межфазных границах устанавливается локальное термодинамическое равновесие, а массоперенос осуществляется объемной диффузией в основной фазе (матрице). Кроме того, не учитывалось влияние упругих напряжений на условия локального равновесия и массоперенос в системе.
Исходными данными для модели служат объемная доля выделений (F) и распределение частиц по размерам в исходном состоянии. Распределения частиц по размерам задаются гистограммами, соответствующими выделениям различного состава. В этих гистограммах k-му размерному классу частиц ставится в соответствие доля частиц, попадающая в данный размерный интервал. Метод основан на использовании приближения среднего поля, согласно которому концентрации всех элементов на некотором расстоянии от частиц одинаковы (одинаковое среднее окружение). К настоящему времени предложен ряд геометрических моделей для построения полевых ячеек. Однако ранее было показано [11], что для небольшой объемной доли выделений расчеты с использованием различных геометрических моделей для полевых ячеек дают приблизительно одинаковые результаты. Так как при моделировании эволюции карбонитридов в сталях обычно рассматривается как раз такой случай (небольшая объёмная доля выделений), мы использовали одну из самых простых моделей [11], в соответствии с которой радиус полевой ячейки, связанной с частицей фазы f l-го размерного интервала, рассчитывается по формуле
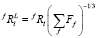 , (1)
, (1)
где Ff – объёмная доля фазы f, а fRl – радиус частицы. Система уравнений диффузии, описывающих потоки вещества в ячейке, связанной с частицей фазы f l-го размерного интервала, для (N + 1)-компонентной системы имеет вид
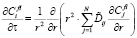 , (2)
, (2)
где 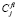 – концентрация i-го компонента в полевой ячейке l-го интервала размеров для выделений состава f;
– концентрация i-го компонента в полевой ячейке l-го интервала размеров для выделений состава f; 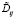 – парциальные коэффициенты взаимной диффузии в матрице, а r – пространственная переменная. При нахождении распределений концентраций элементов использовалось приближение стационарного поля. В этом случае уравнения (2) приобретают вид
– парциальные коэффициенты взаимной диффузии в матрице, а r – пространственная переменная. При нахождении распределений концентраций элементов использовалось приближение стационарного поля. В этом случае уравнения (2) приобретают вид
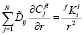 , (3)
, (3)
где 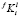 – константа для i-го элемента в ячейке размерного интервала l для выделений состава f. Условия баланса масс на межфазной границе между частицей k-го размерного класса и матрицей имеют вид:
– константа для i-го элемента в ячейке размерного интервала l для выделений состава f. Условия баланса масс на межфазной границе между частицей k-го размерного класса и матрицей имеют вид:
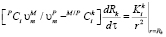 , (4)
, (4)
где 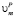 и
и 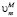 – молярные объемы фазы выделения и матрицы соответственно; M/PCi и PCi – концентрации i-го компонента в матрице на границе с выделением и в выделении соответственно, t – время, а Rk – средний радиус частиц k-го интервала размеров. Условия локального термодинамического равновесия на межфазной границе имеют вид
– молярные объемы фазы выделения и матрицы соответственно; M/PCi и PCi – концентрации i-го компонента в матрице на границе с выделением и в выделении соответственно, t – время, а Rk – средний радиус частиц k-го интервала размеров. Условия локального термодинамического равновесия на межфазной границе имеют вид
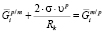 , (5)
, (5)
где 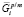 и
и 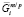 – химические потенциалы i-го элемента на межфазной границе в частице и матрице соответственно; s – удельная поверхностная энергия межфазной границы выделение/матрица; υp – объем одной формульной единицы фазы выделения. Кроме того, из-за использования квазистационарного приближения к этим уравнениям необходимо добавить условие сохранения массы, которому должны удовлетворять рассчитанные средние концентрации компонентов в матрице:
– химические потенциалы i-го элемента на межфазной границе в частице и матрице соответственно; s – удельная поверхностная энергия межфазной границы выделение/матрица; υp – объем одной формульной единицы фазы выделения. Кроме того, из-за использования квазистационарного приближения к этим уравнениям необходимо добавить условие сохранения массы, которому должны удовлетворять рассчитанные средние концентрации компонентов в матрице:
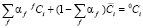 , (6)
, (6)
где αf – мольная доля фазы выделения состава f, 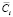 – средняя концентрация растворенного компонента в матрице, 0Ci – концентрация растворенного компонента в сплаве. Средние значения концентраций компонентов в матрице выражаются посредством распределения концентрации в клетках заданных чистых функций следующим образом:
– средняя концентрация растворенного компонента в матрице, 0Ci – концентрация растворенного компонента в сплаве. Средние значения концентраций компонентов в матрице выражаются посредством распределения концентрации в клетках заданных чистых функций следующим образом:
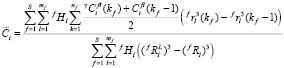 , (7)
, (7)
где mf – число размерных интервалов для частиц фазы f; kf – номер узла в ячейке, связанной с выделениями f-го состава; Nf – число частиц фазы f на единицу объема; S – число избыточных фаз в сплаве; 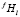 – доля частиц этой фазы, попадающих в этот размерный интервал среди выделений всех составов. Значение
– доля частиц этой фазы, попадающих в этот размерный интервал среди выделений всех составов. Значение 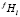 рассчитывается как
рассчитывается как
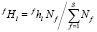 , (8)
, (8)
где Nf – число частиц фазы f в единице объема:
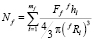 . (9)
. (9)
Для описания зарождения мы использовали подход, развитый Liu и Jonas [13] на основе классической теории зарождения. Liu и Jonas показали, что, если зародыши образуются на дислокациях, то скорость зарождения и энергия Гиббса зародыша критического размера могут быть рассчитаны по формулам
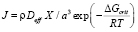 , (10)
, (10)
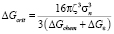 , (11)
, (11)
где ρ – это плотность дислокаций, a – период решётки матрицы, R – универсальная газовая постоянная, T – температура, K. ΔGcrit – изменение энергии системы при образовании одного моля зародышей новой фазы критического радиуса. 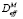 и X – эффективный коэффициент диффузии и концентрация элементa, контролирующего процесс зарождения. В рассматриваемом случае это концентрации карбидообразующих элементов в матрице на границе с карбидными выделениями и эффективные коэффициенты диффузии этих элементов в аустените. σn – удельная поверхностная энергия межфазной границы зародыш/матрица. ς – поправочный множитель к поверхностной энергии межфазной границы, связанный с присутствием дислокаций, который имеет значение между нулем и единицей, ΔGchem и ΔGε – изменения химической свободной энергии и свободной энергии напряжений при образовании единицы объема новой фазы.
и X – эффективный коэффициент диффузии и концентрация элементa, контролирующего процесс зарождения. В рассматриваемом случае это концентрации карбидообразующих элементов в матрице на границе с карбидными выделениями и эффективные коэффициенты диффузии этих элементов в аустените. σn – удельная поверхностная энергия межфазной границы зародыш/матрица. ς – поправочный множитель к поверхностной энергии межфазной границы, связанный с присутствием дислокаций, который имеет значение между нулем и единицей, ΔGchem и ΔGε – изменения химической свободной энергии и свободной энергии напряжений при образовании единицы объема новой фазы.
Методика численных расчетов
Методика численных расчетов была во многом аналогична использовавшейся в работе [11]. Основное отличие состояло в том, что в данном случае рассматривался случай эволюции выделений нескольких избыточных фаз сложного состава. Порядок расчетов был следующим:
1. Расчет размеров полевых ячеек, связанных с частицами всех избыточных фаз и разных размерных интервалов, по формуле (1).
2. Построение пространственных сеток в полевых ячейках для всех фаз и всех размерных интервалов.
3. Расчет концентраций элементов на границах ячеек 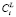 , соответствующих условию сохранения массы (6).
, соответствующих условию сохранения массы (6).
4. Расчет распределений концентраций компонентов в ячейках и скоростей движения межфазных границ для частиц всех избыточных фаз всех размерных интервалов по ур. (3)–(5).
5. Расчет скоростей зарождения выделений для всех избыточных фаз по ур. (10)–(11).
6. Расчет распределений частиц по размерам и объемных долей для всех избыточных фаз на новом временном слое без учета образования новых зародышевых центров.
7. Расчет распределений частиц по размерам и объемных долей для всех избыточных фаз на новом временном слое с учетом процессов зарождения.
Уравнения (3)–(6) решались численно методом Ньютона для систем уравнений с использованием метода конечных разностей для расчета распределений концентраций компонентов в ячейках. Найденные значения объемных долей избыточных фаз и распределений их частиц по размерам использовались как исходные для расчетов на новом временном шаге и т.д. Эта процедура повторялась, пока не достигалось необходимое время. Отдельные этапы расчетов подробно описаны в работах [11, 9, 10].
Распараллеливание вычислений
Для распараллеливания необходимо выбрать такую ветвь алгоритма, чтобы обеспечить, с одной стороны, хорошую масштабируемость для расчётов разной сложности, а с другой стороны, низкие удельные накладные расходы, чтобы повысить коэффициент эффективности распараллеливания. При анализе предложенного алгоритма был сделан вывод, что указанным требованиям в наибольшей степени удовлетворяет процедура расчёта 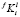 для каждого размерного интервала l выделений состава f при решении системы (4), (5). Эта процедура запускается на каждой итерации поиска
для каждого размерного интервала l выделений состава f при решении системы (4), (5). Эта процедура запускается на каждой итерации поиска 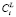 , удовлетворяющих условию сохранения массы (6).
, удовлетворяющих условию сохранения массы (6).
Итоговая реализация распараллеливания представлена на рис. 1 в виде блок-схемы. Этот фрагмент алгоритма выполняется для каждой итерации решения уравнений (6). Чтобы дополнительно снизить удельные накладные расходы на создание программных потоков, для каждого потока заранее формируется список составов выделений и размерных интервалов, для которых в этом потоке будет выполняться поиск 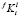 , соответствующих текущей итерации поиска
, соответствующих текущей итерации поиска 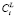 .
.
Для оценки предложенной реализации распараллеливания алгоритма были выполнены тестовые расчёты для комплексных выделений (Ti,Nb)(C,N) и Nb(C,N) для каждого из которых в начальном состоянии было задано 18 размерных интервалов. Коэффициенты ускорения и эффективности (соответственно) рассчитывались по формулам
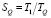 , (12)
, (12)
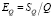 , (13)
, (13)
где TQ – время выполнения параллельной версии алгоритма для числа потоков Q, T1 – время выполнения последовательного алгоритма.
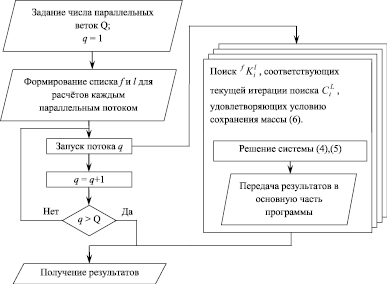
Рис. 1. Блок-схема распараллеливания вычислений на текущей итерации поиска 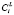
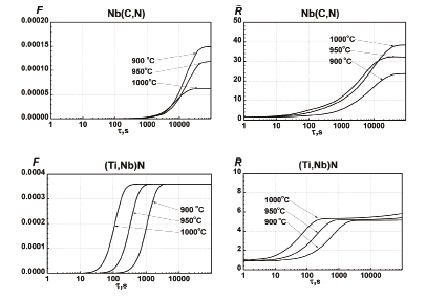
Рис. 2. Изменение объёмной доли и среднего радиуса частиц в процессе отжига при различных температурах для стали состава 0,1 %С, 0,008 %N, 0,02 %Nb и 0,015 %Ti
Тестовый расчёт для оценки эффективности параллельного алгоритма выполнялся на 8-ядерном процессоре AMD FX-2120 (3.1 ГГц). Однако, глядя на результаты для 8-ми-поточного расчёта, надо иметь в виду модульную архитектуру этого процессора – один блок вычислений с плавающей точкой на 2 ядра. Результаты оценки эффективности приведены в таблице.
Коэффициенты ускорения и эффективности
|
Q |
1 |
2 |
3 |
4 |
8 |
|
TQ |
489 |
291 |
235 |
206 |
187 |
|
SQ |
1 |
1,68 |
2,08 |
2,37 |
2,61 |
|
EQ |
1 |
0,84 |
0,69 |
0,59 |
0,33 |
Приведённые в таблице результаты показывают, что эффективность распараллеливания для числа потоков более трёх-четырёх невысока, что объясняется достаточно большим объёмом вычислений, которые необходимо выполнять в основной (последовательной) ветке алгоритма. Тем не менее выигрыш от распараллеливания заметен вплоть до восьми потоков, что говорит о хорошем потенциале применения параллельных вычислений в задачах данного класса.
Результаты расчетов
В качестве примера в настоящей работе были выполнены расчеты эволюции выделений в малоуглеродистых сталях, легированных ниобием и титаном, в процессе выдержки в аустенитной области. Расчёты были проведены в температурном интервале 900÷1000 °C для стали с 0,1 %C, 0,008 %N, 0,02 %Nb и 0,015 %Ti. Состав карбонитридных выделений – Nb(C0.77N0.23)0.97 и (Ti0.85Nb0.15)(C0.01N0.99) – был рассчитан на основе термодинамического моделирования, проведённого с помощью нашей программы IMP Equilibrium. Полученные в результате моделирования зависимости объемной доли и среднего радиуса выделений, для удобства обозначенных как Nb(C,N) и (Ti,Nb)N, приведены на рис. 2.
Заключение
Предложен метод моделирования эволюции карбонитридных выделений в многокомпонентных сталях, основанный на обобщении представленных нами ранее физических моделей для описания эволюции выделений. Метод позволяет прогнозировать поведение нескольких ансамблей карбонитридных выделений сложного состава на стадиях зарождения, роста, растворения и коагуляции. При этом учитывается конечность объёмной доли выделений, полидисперсность ансамбля выделений и диффузионное взаимодействие элементов в матрице. На основе разработанного метода выполнено моделирование эволюции выделений двух составов для системы Fe–Ti–Nb–C–N, моделирующей реальную малоуглеродистую низколегированную сталь.
Предложен метод распараллеливания вычислений при реализации данного алгоритма. Оценка эффективности распараллеливания показала неплохой потенциал применения параллельных вычислений для задач такого типа.
Работа выполнена в рамках государственного задания по теме «Спин» № г/р 01201463330 при поддержке программы фундаментальных исследований УрО РАН (проект № 15-9-2-44) и РФФИ (проект № 16-38-00164).
Библиографическая ссылка
Горбачев И.И., Попов В.В., Пасынков А.Ю. МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ АНСАМБЛЕЙ ВЫДЕЛЕНИЙ НЕСКОЛЬКИХ СОСТАВОВ В МНОГОКОМПОНЕНТНЫХ МНОГОФАЗНЫХ СИСТЕМАХ С РАСПАРАЛЛЕЛИВАНИЕМ ВЫЧИСЛЕНИЙ // Фундаментальные исследования. – 2017. – № 10-3. – С. 423-428;URL: https://fundamental-research.ru/ru/article/view?id=41851 (дата обращения: 26.04.2024).



