В случае кругового осциллятора с потенциальной энергией
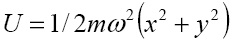
установленное нами обобщённое уравнение Шредингера
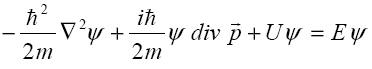 (1)
(1)
в двумерном случае принимает следующий вид
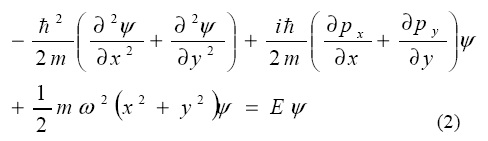
Решение этого уравнения приводит к уровням энергии
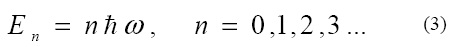
Из (3) следует, что в основном состоянии кругового осциллятора

Согласно нелинейной связи между кинетической, потенциальной и полной энергией
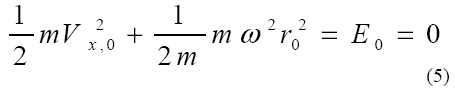
где r2=x2+y2 . Равенство (5) может выполняться только, если Vx,0 = 0 и r0 = 0. Таким образом приходим к выводу, что круговой осциллятор может согласно уравнению (1) находиться в состоянии покоя. Для сравнения заметим, что согласно обычному уравнению Шредингера
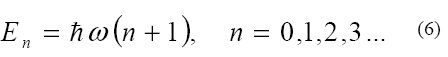
Следовательно, E0 = hω≠ 0 и вместо (4) выполняется равенство
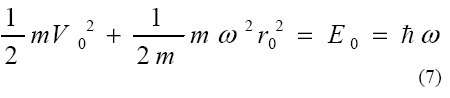
согласно которому при r0 = 0 скорость V0 ≠0. Следовательно, согласно обычному уравнению Шредингера осциллятор не может находиться в состоянии покоя. Это противоречит тому, что при r0 = 0 сила F0 =mω2r0=0 и, следовательно, осциллятор должен находиться в состоянии покоя.
Таким образом, приходим к выводу, что линейное уравнение Шредингера приводит в случае кругового осциллятора (также как и в случае линейного осциллятора) к противоречию.



