Проблема равномерного распределения точек на различных поверхностях имеет большую важность для многих прикладных исследований. Она имеет значение для таких направлений, как математическое моделирование, численные методы, компьютерная графика, технологии армирования и флокирования структурно-неоднородных сред и т.д.
Благодаря своей вариативности и большим прикладным возможностям, в настоящее время проблема вышла за рамки вспомогательной задачи частных интерпретаций и начала приобретать оттенки общетеоретического значения. География работ, посвященных этой проблеме, достаточно широко представлена, а количество работ постоянно увеличивается.
Наиболее четко постановка рассматриваемой задачи, возможные пути ее решения иллюстрируются на одном из частных случаев – проблеме равномерного распределения точек на поверхности сферы [9, 11–13]. С середины XX века в ведущих мировых научных изданиях, таких как журналы «Biometrics», «Annals of Mathematical Statistics» и т.д., стали появляться работы, описывающие различные подходы к решению проблем равномерного распределения точек на поверхности сферы. Как итог многолетнего исследовательского процесса эти алгоритмы стали входить в уже ставшие классическими труды по теории вероятности, математической статистики и методам Монте-Карло [11]. Также следует отметить, что задача равномерного распределения точек на поверхности сферы тесно связана с одной из крупнейших математических проблем XXI века, включенных в список Стивена Смейла (seventh Smales’s problem [7, 8]). Проблеме также посвящена отдельная страница в популярной математической интернет-энциклопедии Wolfram MathWorld [13]. Наряду с феноменологическими подходами к решению задачи равномерного распределения точек на поверхности сферы [7, 8] применяются методы статистического моделирования [9, 12, 13]. Помимо алгоритмов равномерного распределения точек на поверхности сферы в трехмерном «физическом» пространстве также немало работ посвящено решению аналогичной задачи для случая с многомерным пространством. Особо стоит отметить работу «Simulation of random distributions on surfaces» (G. Melfi, G. Schoier, [10]), в которой предлагается метод равномерного распределения точек уже на поверхностях, заданных явным образом в виде функции z = z(x, y).
Алгоритмы равномерного распределения точек на сфере, а также на поверхностях, заданных явным образом в виде функции z = z(x, y), основанные на методе взятия обратной функции для плотности распределения случайной величины и методе Неймана, были изложены авторами в работе [2], в которой также обсуждалась возможность обобщения этих методов для случаев общего задания поверхностей в параметрической форме. Как обобщающий итог исследований, посвященных рассматриваемой проблематике, в данной статье представлен алгоритм равномерного распределения точек на произвольных аналитических поверхностях, которые могут быть заданы в параметрической форме.
В основу алгоритма положен метод статистического моделирования, заключающийся в генерировании координат точек по вычисляемой аналитически функции плотности совместного распределения параметров, соответствующей равномерному распределению точек на поверхности. Для генерирования значения двумерной случайной величины используется обобщенный метод Неймана [8]. Все алгоритмы реализованы в системе компьютерной математики (СКМ) Wolfram Mathematica 7.0, в ней же получены и все визуальные модели.
Общая постановка задачи и методология ее решения
Очевидно, что равномерно распределять точки на плоскости нетрудно, достаточно помещать их в узлы координатной сетки, либо генерировать координаты с помощью эталонного генератора случайной величины с равномерным распределением на заданном отрезке. Также просто решается задача о равномерном распределении точек на разворачиваемых поверхностях, таких как конусы, цилиндры, торсовые поверхности. В случае же с неразворачиваемыми поверхностями – эллипсоид, сфера, тор, параболоид и т.д. – задача значительно усложняется.
Целью исследования являлось получение универсального алгоритма равномерного распределения точек на аналитических поверхностях ненулевой Гауссовой кривизны, заданных параметрическим способом, и иллюстрация равномерных распределений на поверхностях сферы, тора, геликоида, «Падающей капли», бутылки Клейна.
Отметим, что под понятием «равномерное распределение точек на поверхности» понимается такое распределение, при котором на двух произвольных элементах поверхности с одинаковыми площадями располагается одинаковое число точек. Так как предполагается распределение большого количества точек, то для решения задачи применяются методы статистического моделирования. Для каждой поверхности находится функция плотности совместного распределения параметров, удовлетворяющая равномерному распределению точек на рассматриваемой поверхности.
Для нахождения функции плотности совместного распределения используются возможности символьной математики пакета Wolfram Mathematica 7.0. Эти средства позволяют усиливать численные алгоритмы (численное интегрирование, нахождение экстремумов функций и т.д.) символьными вычислениями (например, нахождения производных в общем виде), что делает алгоритмы предельно универсальными.
Нахождение функции плотности совместного распределения вероятностей при описании равномерного распределения точек на произвольных поверхностях
Пусть поверхность задана параметрическими уравнениями x = x(u, v), y = y(u, v), z = z(u, v) на области D = {u1 ≤ u ≤ u2; v1 ≤ v ≤ v2}. Необходимо найти аналитически f(u, v) – функцию плотности совместного распределения параметров u, v, соответствующую равномерному распределению точек на рассматриваемой поверхности.
В случае, когда точки равномерно распределяются на поверхности, вероятность попадания произвольной точки А на элемент поверхности dS с одной стороны равна:
![]()
где, согласно [1, 3],
![]()
![]()
(E, F, G – коэффициенты первой квадратичной формы поверхности). Следовательно,
![]()
С другой стороны, вероятность попадания точки А на элемент поверхности равна
![]()
Принимая во внимание вышеизложенные соотношения, получаем равенство:
![]()
Откуда окончательно находим искомую функцию плотности совместного распределения параметров, соответствующую равномерному распределению точек на рассматриваемой поверхности:
![]()
Генерируя значения параметров u, v с использованием функции f(u, v), получим равномерное распределение точек на поверхности.
Метод Неймана генерирования многомерной случайной величины по известной функции плотности совместного распределения параметров
Для моделирования одномерной случайной величины по функции плотности распределения применяются различные методы [5, 11]. Например, метод взятия обратной функции удобен в случаях, когда можно получить аналитически обратную функцию. Однако применение данного метода усложняется в случаях многомерных распределений зависимых случайных величин. Универсальным методом генерирования случайных величин по известным плотностям распределения является метод Неймана (метод усечения), суть которого рассмотрим сначала на примере одномерной случайной величины. В этом случае алгоритм реализуется следующим образом [5, 11]:
1. Функция плотности распределения вписывается в прямоугольник.
2. Генерируются два независимых числа эталонным генератором случайной величины с равномерным распределением на интервале (0, 1) и масштабируются по сторонам прямоугольника.
3. Если полученная точка попадает в область под графиком плотности распределения, то точка принимается, иначе отбрасывается.
4. Повторяются действия 2–3 до тех пор, пока не будет сгенерировано необходимое число точек.
При переходе к многомерным случаям процедура генерации сохраняется с учетом изменения размерности пространства. Для двумерных случайных величин, соответствующих нашему случаю, сохраняется наглядность алгоритма, так как процедура усечения осуществляется в трехмерном «физическом» пространстве. В этом случае алгоритм реализуется следующим образом:
1. Определяется ![]() – максимальное значение функции f(u, v) на области D = {u1 ≤ u ≤ u2; v1 ≤ v ≤ v2}.
– максимальное значение функции f(u, v) на области D = {u1 ≤ u ≤ u2; v1 ≤ v ≤ v2}.
2. Генерируются числа
![]() ,
, ![]() ,
,
где R – эталонный генератор случайного числа с равномерным распределением на интервале (0, 1);
3. Выполняется проверка: если
![]() ,
,
где R – эталонный генератор случайного числа с равномерным распределением на интервале (0, 1), то точка принимается, в противном случае отбрасывается.
4. Повторяются действия 2–3 до тех пор, пока не будет сгенерировано необходимое число точек.
Визуализация результатов
Описанные выше алгоритмы были реализованы в пакете Wolfram Mathematica 7.0, который позволяет также строить визуальные модели, что является удобным для контроля работы программы и демонстрации результатов. Ниже представлены некоторые визуальные результаты работы алгоритма.
На рис. 1 представлена поверхность сферы и равномерное распределение 15000 точек на ней. Поверхность сферы задана уравнениями:
![]()
![]()
![]()
где 0 ≤ u ≤ π, 0 ≤ v ≤ 2π.
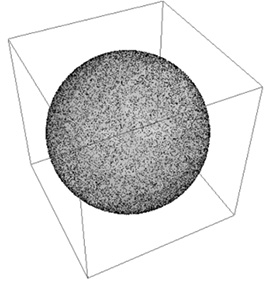
Рис. 1. Равномерное распределение 15000 точек на поверхности сферы, ViewPoint: {1,2,2}
На рис. 2 представлена поверхность тора и равномерное распределение 20000 точек на ней. Поверхность тора задана уравнениями:
![]()
![]()
![]()
где 0 ≤ u ≤ 2π, 0 ≤ v ≤ 2π.
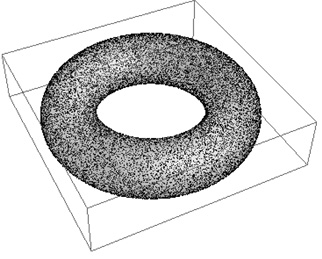
Рис. 2. Равномерное распределение 20000 точек на поверхности тора, ViewPoint: {1,2,2}
На рис. 3 представлена поверхность геликоида и равномерное распределение 15000 точек на ней. Поверхность геликоида задана уравнениями:
![]()
![]()
![]()
где 0 ≤ u ≤ 2π, 0 ≤ v ≤ 2π.

Рис. 3. Равномерное распределение 15000 точек на поверхности геликоида, ViewPoint: {1,2,2}
На рис. 4 представлена поверхность «Падающая капля» и равномерное распределение 20000 точек на ней. Поверхность «Падающая капля» задана уравнениями [4]:
![]()
![]()
![]()
где 0 ≤ u ≤ 2π, 0 ≤ v ≤ 1.
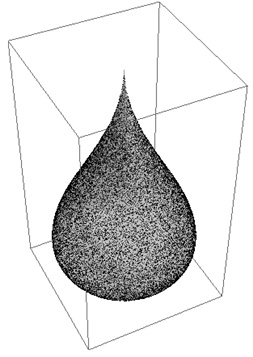
Рис. 4. Равномерное распределение 20000 точек на поверхности «Падающая капля», ViewPoint: {1,2,2}
На рис. 5 представлена поверхность бутылки Клейна и равномерное распределение 20000 точек на ней. Поверхность бутылки Клейна задана уравнениями [6]:
![]()
![]()
![]()
где –π/2 ≤ π/2 , 0 ≤ v ≤ 2π.
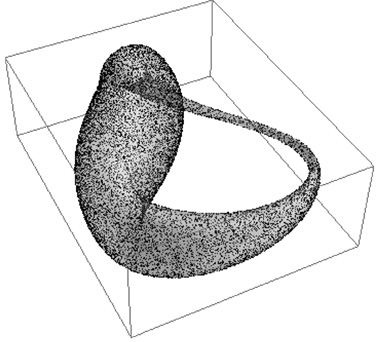
Рис. 5. Равномерное распределение 15000 точек на поверхности бутылки Клейна, ViewPoint: {1,2,2}
Визуальный анализ полученных результатов равномерного распределения точек на поверхностях различных типов подтверждает правильность работы алгоритма.
Выводы
Приведенные конкретные примеры реализации предложенного метода равномерного распределения точек на аналитических поверхностях подтверждают его высокую эффективность и универсальность. Визуальный анализ полученных графических результатов свидетельствует о равномерном распределении точек на поверхностях. Предложенный алгоритм может быть обобщен для генерирования неравномерного распределения точек на заданной поверхности.
Рецензенты:
Берестова С.А., д.ф.-м.н., доцент, заведующая кафедрой теоретической механики Института фундаментального образования Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Сесекин А.Н. д.ф.-м.н., профессор, заведующий кафедрой прикладной математики Уральского энергетического института Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 19.02.2013.



