Современные логистические складские комплексы (ЛСК) представляют собой сложно организованные хозяйственные объекты, ориентированные на управление грузопотоками большой емкости, в том числе на дистрибуцию товаров, и, вследствие этого, играют важную роль в экономической сфере деятельности. Особое внимание привлекают региональные складские комплексы, так как сегодня значительное число крупных российских производственных компаний, торговых сетей и иностранных ритейлеров выбирают расширение сбыта продукции в регионах в качестве основного направления своего развития и остро нуждаются в качественных масштабных услугах складской логистики. Тенденция развития современных ЛСК заключается в постоянном расширении множества складских операций и повышении уровня их сложности. Вследствие этого эффективное управление складом становится исключительно важной и сложной проблемой. Чтобы справиться с неизбежным ростом числа операций и их усложнением, управление ЛСК должно базироваться на системном подходе. В этой связи важнейшими задачами складского менеджмента становятся анализ и оптимизация организационно-функциональной структуры как эксплуатируемых, так и проектируемых ЛСК.
Одним из наиболее эффективных подходов к анализу процессов функционирования экономических объектов и управления ими является математическое моделирование. К настоящему времени имеется широкий спектр экономико-математических моделей для различных отраслей производства, бизнеса и управления. Зачастую основное внимание в методах исследования экономических объектов уделяется статистическим моделям, в то время как многие важные особенности поведения таких объектов могут проявиться только в динамике. Сложность динамической структуры современных экономических объектов, обусловленная большим количеством важных характеристик процессов их функционирования и связей между ними, требует построения согласованного семейства моделей, позволяющих проводить исследование этих объектов на разных уровнях детализации, и зачастую приводит к значительным техническим и методическим трудностям использования такого семейства моделей.
Современные системы управления складскими процессами класса WMS (Warehouse Management System) представлены такими программными комплексами, как Фолио WMS, AZ.WMS, SmartStock.WMS, Solvo.WMS, Radio Beacon WMS и многими другими. Такого рода программные комплексы включают в себя средства моделирования складских процессов, но имеют, как правило, узкую специализацию и не пригодны для моделирования многих логистических процессов, возникающих при совместном осуществлении функций складирования, транспортировки и торговли.
Логистические системы класса ERP (Enterprise Resource Planning), такие как, например, система Microsoft Axapta, являются мощными инструментами управления внутренними процессами предприятия, включая работу ЛСК. Однако такие коммерческие системы ориентированы в основном на крупные предприятия. Кроме того, в этих комплексах и системах используются, как правило, аналитические методы моделирования, не позволяющие учесть все детали технологических процессов и исследовать их в динамике в отличие от имитационного моделирования.
Более того, при решении практических задач часто возникает необходимость учета и обработки дополнительной информации о событиях, явлениях, процессах и их взаимосвязях, не укладывающихся в модели предметных областей используемых логистических систем. Таким образом, возникает необходимость применения дополнительных средств формулировки и решения «нестандартных» (с точки зрения используемых логистических систем) задач. Для их решения существует множество различных программных средств. Проблема заключается в разработке методики согласованного использования этих программных средств.
Методика решения задач складской логистики
Предлагаемая авторами статьи методика основана на подходах к моделированию сложных систем, представленных в работах [4, 12] и ориентирована на использование распределенной вычислительной среды для проведения многовариантных расчетов. Данная методика направлена на интеграцию аналитического и имитационного моделирования, что позволяет более детально анализировать деятельность складского комплекса в динамике и выполнять быструю точечную реализацию дополнительных средств моделирования процессов функционирования ЛСК, не представленных в используемых системах управления этими комплексами.
Рассмотрим основные этапы реализации этой методики.
1 этап. Построение концептуальной модели и постановка задачи. На данном этапе предлагается использовать инструменты теории массового обслуживания. Целью теории систем массового обслуживания (СМО) является выработка рекомендаций по рациональному построению системы массового обслуживания и рациональной организации их работы и регулированию потока заявок, поэтому исследование СМО существенно при анализе функционирования такой сложной системы, как логистический складской комплекс. Отсюда вытекают задачи: установление зависимостей работы СМО от ее организации, характера потока заявок, числа каналов и их производительности, правил работы СМО. Для успешного выполнения первого этапа целесообразно разбить его на составляющие (подэтапы):
- структурный анализ предметной области: построение концептуальной модели в терминах предметной области, выявление характеристик объектов предметной области и связей между ними;
- постановка задачи имитационного моделирования системы: формулировка задачи исследования конкретной системы с учетом актуальности такой задачи и необходимости имитационного моделирования, имеющихся ресурсов, масштаба задачи и возможности разбиения ее на подзадачи;
- анализ задачи моделирования системы: проведение анализа, включая выбор критериев оценки эффективности процесса функционирования системы, выполнение предварительного анализа последующих этапов моделирования;
- определение требований к исходной информации и организация ее сбора: формулировка требований к исходной информации об объекте моделирования и в случае необходимости получение недостающей информации, анализ имеющихся экспериментальных данных, выбор методов и средств предварительной обработки информации о системе;
- определение параметров и переменных модели: необходимо определить параметры системы, входные и выходные переменные, воздействия внешней среды;
- установление основного содержания модели: определение основного содержания модели и выбор метода построения модели системы с учетом формулировки задачи моделирования, структуры системы и алгоритмов ее поведения, воздействия внешней среды, возможных методов и средств решения задачи моделирования.
2 этап. Формализация задачи. Основным содержанием этого этапа является переход от словесного описания объекта к его математической модели как системы массового обслуживания. Математическая модель представляет собой совокупность соотношений (например, уравнений, логических условий, операторов), определяющих характеристики процесса функционирования системы в зависимости от структуры системы, алгоритмов поведения, параметров системы, воздействий внешней среды, начальных условий и времени. Математическая модель является результатом формализации процесса функционирования исследуемой системы, т.е. построения формального (математического) описания процесса с необходимой в рамках проводимого исследования степенью приближения к действительности. Модель должна быть адекватной, иначе невозможно получить положительные результаты решения поставленной задачи. Адекватной считается модель, которая с определенной степенью приближения отражает процесс ее функционирования во внешней среде [12]. Данный этап состоит из следующих подэтапов:
- формулирование законов, связывающих основные объекты модели и описывающих динамику её функционирования;
- запись на математическом языке всех соотношений и зависимостей, присущих идеализированному объекту, в том числе формулирование математических задач, к которым приводит математическая модель.
3 этап. Построение имитационной модели. Данный этап представляет собой практическую деятельность, направленную на реализацию идей и математических схем в виде имитационной модели, ориентированной на использование конкретных программно-технических средств, и включает в себя следующие подэтапы:
- построение логической схемы модели: необходимо разработать логическую структуру модели процесса функционирования системы по блочному принципу для обеспечения необходимой гибкости модели;
- реализация математических соотношений в имитационной модели: проведение соответствия между математической постановкой задачи и переменными в имитационной среде;
- проверка достоверности модели системы: проверяется возможность решения поставленной задачи, полнота и точность отражения замысла в логической схеме, правильность используемых математических соотношений;
- выбор инструментальных средств для моделирования: окончательное решение вопроса о том, какое программное обеспечение целесообразно использовать для реализации модели системы;
- проведение программирования модели: на основе логической схемы модели строится схема программы и программируется в соответствии с выбранным языком (системой);
- проверка достоверности программы: проверка отдельных частей программы при решении различных тестовых задач; объединение всех частей программы и проверка ее в целом на контрольном примере моделирования варианта системы.
4 этап. Планирование вычислительного эксперимента. Составление плана проведения эксперимента с указанием комбинаций переменных и параметров, для которых проводится моделирование системы. Имитационное моделирование представляет собой статистический эксперимент, цель которого – получить достоверный результат с заданной точностью. В общем случае количество прогонов модели, необходимое для получения оценок наблюдаемой переменной с заданной точностью, зависит от следующих факторов: вида распределения наблюдаемой переменной, коррелированности между собой элементов выборки, наличия и длительности переходного периода [12]. Для выполнения данного этапа необходимо реализовать следующие подэтапы:
- стратегическое планирование вычислительного эксперимента: необходимо разработать условия проведения эксперимента, определить измеряемые величины, существенные факторы, их сочетания и уровни каждого фактора;
- тактическое планирование вычислительного эксперимента: основной задачей тактического планирования является обеспечение результатам компьютерного эксперимента заданных точности и достоверности;
- определение требований к вычислительным средствам: необходимо сформулировать требования по времени использования вычислительных средств, оценить возможность проведения расчетов на одном компьютере или в распределенной вычислительной среде.
5 этап. Проведение эксперимента. После составления имитационной модели и плана проведения вычислительного эксперимента можно приступить к расчетам, которые включают в себя следующие подэтапы:
- контрольные расчеты: контрольные расчеты выполняются для проверки имитационной модели и определения чувствительности результатов к изменению исходных данных;
- рабочие расчеты: проведения рабочих расчетов по составленной и отлаженной программе;
- анализ результатов моделирования: вычисление статистических характеристик перед выводом результатов моделирования повышает эффективность вычислительного эксперимента и сводит к минимуму обработку выходной информации для интерпретации результатов моделирования [8–10, 13–15];
- представление результатов моделирования: необходимо уделить внимание форме представления окончательных результатов моделирования для каждого конкретного случая (таблицы, графики, диаграммы, схемы).
Как отмечено в [12], проведение рабочих и контрольных расчетов обычно включают в себя:
а) подготовку наборов исходных данных;
б) проверку исходных данных;
в) проведение расчетов;
г) получение выходных данных, т.е. результатов моделирования.
Для проведения многовариантных расчетов используется распределенная вычислительная среда [5, 11], позволяющая существенно сократить общее время проведения вычислительного эксперимента за счет параллельного выполнения этих расчетов.
6 этап. Интерпретация результатов моделирования. Здесь необходимо перейти от информации, полученной в результате вычислительного эксперимента с имитационной моделью, к информации применительно к объекту моделирования, на основании которой и будут делаться выводы относительно характеристик процесса функционирования исследуемого ЛСК. Данный этап состоит из следующих подэтапов:
- перевод результатов моделирования в исходную шкалу измерений: полученные результаты необходимо перевести в размерность реальных физических величин;
- описание ключевых особенностей модели, результатов проведения вычислительного эксперимента;
- проверка гипотез и предположений, выдвинутых на этапе постановки задачи: в зависимости от целей исследования и вида, получаемых при моделировании результатов, могут использоваться методы корреляционного, дисперсионного и регрессионного анализа [6];
- выводы и рекомендации по практическому использованию результатов моделирования: результаты моделирования отражают основные особенности функционирования объекта и позволяют качественно и количественно оценить его поведение.
Разработана инструментальная система [3], обеспечивающая частичную или полную автоматизацию всех этапов методики, рассмотренной выше. Данная методика была использована для решения ряда практических задач складского менеджмента [1, 2, 7].
Вычислительный эксперимент
Решение задачи складской логистики обязательно включает в себя: подготовку исходных данных, формирование паспорта задания, сбор данных и анализ собранной информации. Поэтому анализ эффективности описанной выше методики был проведен на основе оценки времени, затраченного для решения задач с использованием данной методики и без нее. Данные получены эмпирическим путем при проведении ряда экспериментов.
Время выполнения i-го задания задано соотношением
ti = αi + βi + γi + δi ,
где αi − время, необходимое для подготовки исходных данных для выполнения i-го задания; βi − время формирования паспорта i-го задания; γi − время сбора данных о выполненном i-м задании; δi − время анализа данных i-го задания. Тогда оценка времени, затрачиваемого на решение задачи, содержащей k заданий, определяется по формуле
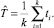
Как показывают результаты, приведенные в таблице, применение описанной в статье методики в значительной степени сокращает трудозатраты на решение задач складского менеджмента, что позволяет сделать вывод об эффективности данной методики для решения подобных задач.
Заключение
В статье представлена методика решения задач складской логистики, основанная на применении методов и средств системного анализа. Особенностью данной методики является интегрированное применение аналитического и имитационного моделирования. Предложенная методика позволяет анализировать деятельность логистического складского комплекса в динамике и дает возможность решать «нестандартные» (с точки зрения программных комплексов ERP и WMS классов) задачи складского менеджмента. При решении ряда практических задач показана эффективность применения данной методики.
Результаты оценки времени выполнения этапов решения задачи складской логистики
|
Этапы |
|
|
|
с использованием предложенной методики |
без использования предложенной методики |
|
|
Подготовка данных |
10−60 |
10−120 |
|
Формирование паспорта задания |
1−4 |
10−300 |
|
Сбор данных |
1−2 |
10−120 |
|
Анализ данных |
1−4 |
10−90 |
Рецензенты:
Кузьмин О.В., д.ф-м.н., профессор, заведующий кафедрой теории вероятностей и дискретной математики Иркутского государственного университета, г. Иркутск;
Лакеев А.В., д.ф-м.н., профессор, ведущий научный сотрудник Института динамики систем и теории управления СО РАН, г. Иркутск.
Работа поступила в редакцию 25.12.2013.




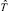 – оценка времени выполнения этапа для одного варианта вычислительного эксперимента в с
– оценка времени выполнения этапа для одного варианта вычислительного эксперимента в с