Работа посвящена анализу математической модели блока синтеза этаноламинов и задаче оптимального управления процессом синтеза.

Блок синтеза этаноламинов включает реактор-смеситель и реактор вытеснения, соединенные между собой материальными потоками (рис. 1).

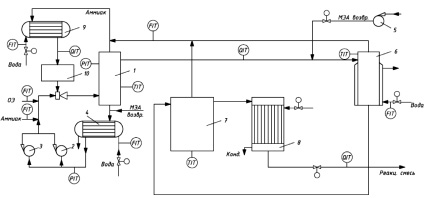
Рис. 1 Принципиальная схема процесса синтеза этаноламинов: 1 – аппарат смешения; 2,3 – насосы; 4 – теплообменник; 5 – насос; 6 – реактор вытеснения; 7 – сепаратор; 8 – испаритель; 9 – теплообменник; 10 – емкость

Математическая модель блока синтеза разработана для каскада двух реакторов: смешения и вытеснения, установленных последовательно и работающих в непрерывном режиме (рис. 2).

Входными переменными модели являются расход потока входных компонентов, а именно окиси этилена (ОЭ), моноэтаноламина (МЭА), аммиака (NH3) и возвратного аммиака.

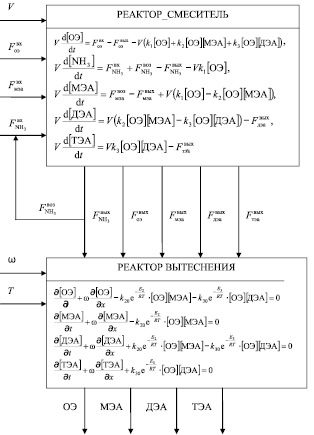
Рис. 2 Блок-схема математической модели блока синтеза этаноламинов

Выходные параметра – это состав реакционной смеси на выходе блока синтеза, к которым относятся моноэтаноламины (МЭА), диэтаноламины (ДЭА) и триэтаноламины (ТЭА).

Процесс проводится при многократном избытке аммиака, который циркулирует в узле синтеза, и контроль за расходом возвратного аммиака позволит рационально использовать поступление свежего аммиака.

На основании вышеизложенного можно предложить системы оптимального управления узлом синтеза этаноламинов.

Подача МЭА в реактор-смеситель стабилизирована, подача аммиака со склада корректируется с учетом возвратного аммиака.

Подача окиси этилена корректируется на основе результатов аналитического контроля выходного потока из смесителя с помощью математической модели реактора-смесителя для достижения оптимального состава реакционной смеси на выходе смесителя. Критерием оптимальности является один из компонентов реакционной смеси на выходе из реактора, чаще моноэтаноламин:

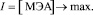
Решение поставленной задачи обеспечивается математической моделью объекта в виде системы обыкновенных дифференциальных уравнений:

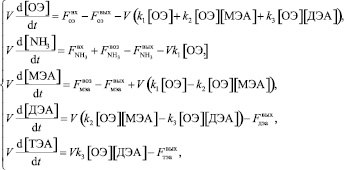
взятой для стационарного состояния объекта

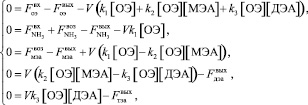
где 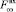– расход входного потока окиси этилена; 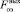– расход выходного потока окиси этилена; 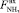– расход входного потока аммиака; 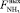– расход выходного потока аммиака; 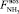– расход возвратного аммиака; 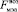– расход возвратного моноэтаноламина; 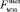– расход выходного потока МЭА; 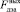– расход выходного потока ДЭА; 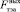– расход выходного потока ТЭА; V – объем окиси этилена.

Поиск оптимума осуществляется путем численного решения системы нелинейных алгебраических уравнений с вариацией входного параметра управления 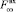(подача ОЭ) одним из однопараметрических методов оптимизации, и с последующей корректировкой задания регулятору расхода ОЭ.

Оптимальный состав реакционной смеси на выходе из узла синтеза достигается регулированием температуры в реакторе вытеснения за счет подачи пара, определяемой с помощью регрессионной математической модели: 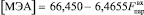, полученной в ходе статистического анализа объекта управления.

Рецензенты:

Никандров И.С., д.т.н., профессор кафедры «Автомобильный транспорт и механика» Дзержинского политехнического института (филиал) НГТУ, ФГБО ВПО «Нижегородский государственный технический университет им. Р. Е. Алексеева», г. Дзержинск;

Сидягин А.А., д.т.н., профессор кафедры «Машины и аппараты химической и пищевой производств», ФГБО ВПО «Нижегородский государственный технический университет им. Р. Е. Алексеева», Дзержинский политехнический институт (филиал), г. Дзержинск.

Работа поступила в редакцию 25.12.2013.