Высокий уровень математической подготовки достигается в процессе обучения, ориентированного на широкое раскрытие связи математики с окружающим миром, с практикой. Одним из разделов математики, наиболее полно отвечающим данному требованию в силу своей специфики отражения реальной действительности, является, на наш взгляд, геометрия. При изучении систематического курса геометрии основной школы большое значение, бесспорно, занимают задачи на построение. Трудно переоценить роль задач на построение в формировании математического мышления и научного мировоззрения студентов и школьников.
Однако проведенное констатирующее исследование показало, что практические задачи на построение вызывают значительные трудности у учеников и студентов вузов. Наибольшую трудность обучаемые испытывают в первую очередь на этапе формализации практической задачи, во вторую очередь при решении составленной математической модели – задачи на построение. На наш взгляд, это связано с тем, что, во-первых, задачи на построение с практическим содержанием часто являются задачами повышенной трудности; во-вторых, недостатком внимания со стороны как школьных учителей математики, так и преподавателей геометрии к задачам такого рода; в-третьих, недостаточной разработанностью методики обучения решению задач на построение с практическим содержанием.
Поэтому при обучении решению практических задач на построение необходимо учитывать три важных момента: решение собственно задач на построение, решение практических задач, составление и решение практических задач на построение, механизм составления которых описан в статье [4]. Первый аспект подробно рассмотрен одним из авторов в монографии [1], второй аспект частично освещен в учебных пособиях [2; 6], а третий – в монографии авторов данной статьи [3].
Таким образом, цель нашего исследования – разработка методических указаний по обучению студентов и учащихся решению задач на построение с практическим содержанием. Для достижения поставленной цели были использованы следующие методы исследования: теоретический (анализ психолого-педагогической и научно-методической литературы), социометрический (наблюдение, беседа, анкетирование), статистический (математическая обработка результатов исследования).
Разработанные нами методические указания включают в себя рассмотрение механизма составления и решения практических задач на построение [4]; использование комплекса наводящих вопросов по осуществлению этапа анализа в задачах на построение и обобщенного правила-ориентира для решения задач на построение [1]; использование разработанных авторами комплекса задач на построение с практическим содержанием [2; 3]; применение краеведческого материала при составлении и решении задач практического содержания для реализации национально-регионального компонента [5]; использование при обозначении геометрических объектов в таких задачах маркеров (мелков) разных цветов для лучшего понимания их условия; подведение обучаемых к составлению математической модели практической задачи на этапе формализации с помощью приема «использование разумных вопросов».
Рассмотрим данный прием на примере следующих задач.
Задача 1. На карте города изображены три пересекающиеся дороги BC, CA, AB. Построить кольцевую дорогу, касающуюся трех данных дорог.
Задача 2. Пруд, находящийся неподалеку от деревни, имеет округлую форму. Дорожникам надо построить прямую дорогу к пруду от деревни так, чтобы дорога прилегала к пруду.
Задача 3. Через данное село и шоссе, не проходящее через село, построить проселочную дорогу так, чтобы расстояние от населенного пункта до шоссе было минимальным.
Рассмотрим, какие геометрические фигуры могут служить образами реальных объектов, приведенных в этих задачах, и каковы отношения между этими образами. В задаче 1 образами могут быть следующие геометрические фигуры: три данные несовпадающие прямые и окружность; отношение – окружность, касающаяся данных прямых. В задаче 2 образами могут быть следующие геометрические фигуры: окружность, точка вне окружности и касательная; отношение – касательная к окружности, проходящая через точку. В задаче 3 – геометрические фигуры: прямая, точка, не лежащая на ней, и искомая прямая; отношение – искомая прямая, проходящая через точку перпендикулярно к первой прямой.
Разумными вопросами к данным задачам могут быть следующие:
- Образами каких геометрических фигур (точки, прямой, окружности) могут служить следующие реальные объекты?
- Какими отношениями: принадлежности, равноудаленности, касания и т.п. можно заменить зависимости между реальными объектами?
Следует отметить, что предложенные вопросы позволяют иногда к нескольким практическим задачам сформулировать одну математическую задачу. Сформулируем математические задачи к предложенным выше практическим задачам.
Задача 1′. Провести окружность, касающуюся трех данных несовпадающих прямых BC, CA, AB.
Задача 2′. К данной окружности построить касательную, проходящую через данную точку вне окружности.
Задача 3′. Даны прямая a и точка M, не лежащая на ней. Постройте прямую, проходящую через точку M и перпендикулярную к прямой a.
Отметим, что решение любой практической задачи обычно состоит из трех этапов:
1) этап формализации;
2) этап решения внутри математической модели;
3) этап интерпретации.
Уже на первом этапе студенты (и учащиеся) испытывают трудности в создании математической модели рассматриваемой задачи: в анализе условия задачи, в переводе практической задачи на язык математики – получении геометрической задачи на построение, в анализе условия самой задачи на построение. Для примера рассмотрим следующую задачу.
Задача 4. На берегу реки требуется построить водонапорную башню для снабжения водой двух сел так, чтобы общая длина труб от водонапорной башни до обоих сел была наименьшей.
Сконструируем геометрическую задачу.
Задача 4′. Дана прямая MN, две точки А и В, расположенные по одну сторону от этой прямой. На прямой найти точку, сумма расстояний которой до данных точек была бы наименьшей (где MN – образ реки, А и В – местоположение сел).
Анализ
Изобразим данные геометрической задачи (рис. 1, а). Кратчайшее расстояние – это отрезок прямой. Отсюда понятно построение.
Построение:
1. Построим точку Т, симметричную точке В относительно прямой MN (рис. 1, б).
2. Проведем прямую АТ.
3. Найдем точку пересечения С с прямой MN. Водонапорную башню следует строить в точке С (рис. 1, в).
а 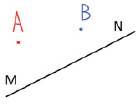 б
б 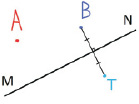 в
в 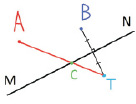
Рис. 1. а ‒ данные условия задачи; б ‒ кратчайшее расстояние; в ‒ местоположение водонапорной башни
Задача 5. Необходимо соединить шоссейной дорогой, включая постройку моста через реку, два села. Как должна пройти эта дорога, чтобы путь между селами был кратчайшим? Сконструируем на основе этой задачи чисто геометрическую задачу.
Задача 5′. Две точки А и В расположены по разные стороны от полосы MNPT, где прямые MN и PT параллельны. Соединить точки А и В ломаной так, чтобы одно из звеньев было перпендикулярно прямой MN, а длина ломаной была наименьшей (MN и PT – образы берегов реки, точки А и В – это месторасположение сел).
Анализ
Пусть MN и PT – образы берегов реки, точки А и В – это расположение сел (рис. 2, а).
Построение
1. Построим отрезок АК, перпендикулярный MN так, что АК равно расстоянию между прямыми MN и PT (рис. 2, б).
а 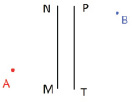 б
б 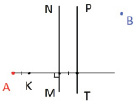 в
в 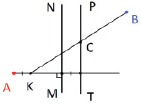
г 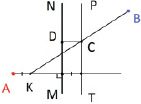 д
д 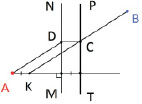
Рис. 2. а ‒ данные условия задачи; б ‒ построение отрезка AK; в ‒ построение точки пересечения прямых КВ и PT; г ‒ построение прямой, перпендикулярной MN; д ‒ построение искомой дороги
2. Проведем прямую КВ, найдем ее точку пересечения с прямой PT – точка С (рис. 2, в).
3. Проведем прямую CD, перпендикулярную MN (рис. 2, г).
4. Соединим точки A и D. Искомая дорога пройдет по ломаной ADCB (рис. 2, д).
Задача 6. Жители селений A и B просили сделать остановку на кольцевой дороге на одинаковом расстоянии от этих сел. Найти место для остановки.
В результате анализа условия данной задачи выделяются три объекта: села A и B, кольцевая дорога; два отношения: принадлежности (остановка, расположенная на кольцевой дороге) и равноудаленности (остановка, равноудаленная от сел). При переводе этой практической задачи на язык математики получаем следующую геометрическую задачу.
Задача 6′. На данной окружности построить точку, равноудаленную от двух данных точек, не принадлежащих данной окружности.
В результате анализа условия полученной задачи на построение выделяются следующие геометрические фигуры: две данные точки A и B и данная окружность (рис. 3, а); и два отношения: принадлежности (точка, принадлежащая окружности) и равноудаленности (точка, равноудаленная от точек A и B). Анализ также показал, что полученная задача является задачей на положение, так как точки A, B и окружность определены по положению в пространстве.
а 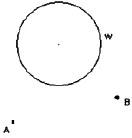 б
б 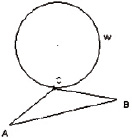 в
в 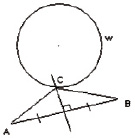
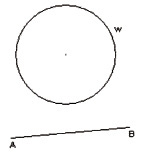 д
д 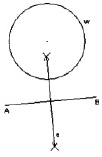 е
е 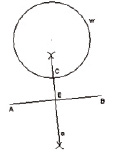
 з
з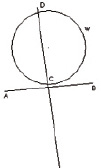 и
и 
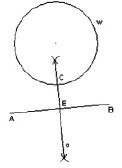
Рис. 3. а ‒ данные условия задачи; б ‒ искомая точка; в ‒ анализ построения искомой точки; г ‒ построение отрезка AB; д ‒ построение серединного перпендикуляра; е ‒ построение искомой остановки; ж ‒ исследование: единственное решение; з ‒ исследование: два решения; и ‒ исследование: нет решений
Второй этап – решение внутри математической модели представляет не меньшую трудность, так как требуется решить задачу на построение, что очень часто вызывает большие затруднения. Решение задачи на построение на данном этапе, на наш взгляд, должно включать все этапы классической схемы решения задач такого вида, то есть анализ, построение, доказательство и исследование. Вернемся к предложенной выше задаче.
Анализ
Пусть данная задача на построение решена, то есть на окружности построена точка C, равноудаленная от точек A и B (рис. 3, б).
Так как точка С равноудалена от точек А и В, следовательно, С лежит на серединном перпендикуляре к отрезку АВ, кроме того, по условию точка С принадлежит данной окружности. Отсюда понятно построение (рис. 3, в).
Построение
- Соединим точки А и В (рис. 3, г).
- Строим серединный перпендикуляр а (рис. 3, д).
- w∩a = C (рис. 3, е). Таким образом, C – искомая точка.
Доказательство:
∆ACE = ∆BCE (по двум катетам: СЕ – общий, АЕ = ЕВ, т.к. точка Е – середина отрезка). Из равенства треугольников следует, что АС = СВ.
Исследование:
a) решение существует и будет единственным, если существует точка пересечения середины перпендикуляра и окружности (рис. 3, ж).
б) если перпендикуляр и окружность имеют две точки пересечения – это точки C и D, то задача имеет два решения (рис. 3, з).
в) нет решений, когда расстояние от центра окружности до серединного перпендикуляра к АВ больше радиуса окружности (рис. 3, и).
Третий этап является, на наш взгляд, не менее важным при решении практических задач, так как именно на этом этапе анализируются полученные решения на соответствие их реальным ситуациям. Например, в предложенной задаче, в случае, когда окружность пересекается с серединным перпендикуляром в двух точках C и D – случай б ‒ в проведенном исследовании, нас устраивает только одна точка C, так как остановка должна находиться ближе к пунктам A и B. Кроме того, данный этап очень важен для обучения составлению практических задач при наличии математической задачи, в нашем случае задачи на построение.
В заключение отметим, что предложенные методические указания способствуют преодолению выделенных трудностей при обучении студентов и учащихся решению практических задач на построение.
Рецензенты:
Гусев В.А., д.п.н., профессор, заведующий кафедрой теории и методики обучения математике Московского педагогического государственного университета, г. Москва;
Михайлов П.Н., д.ф.-м.н., профессор, ученый секретарь, ГАНУ «Институт прикладных исследований республики Башкортостан», г. Стерлитамак.
Работа поступила в редакцию 06.03.2014.



