Психологи, педагоги и методисты давно доказали, что для эффективной реализации целей образования нужно использовать в учебном процессе систему задач с научно обоснованной структурой, в которой место и порядок каждого элемента строго определены и отражают структуру и функции этих задач.
Так, всякая задача сама по себе обычно представляет некоторое изолированное утверждение или требование и предполагает выполнение определённых действий для её решения. Кроме того, каждая математическая задача, как и любая задача вообще, имеет определённый набор связанных с ней задач, определённую окрестность – по содержанию, методам рассуждений, кругу используемых понятий. Более того, каждая задача входит в целую совокупность – букет окрестностей, связанных с той или иной её особенностью, а выбор одной из этих окрестностей задачи для достижения тех или иных дидактических целей определяется конкретными условиями обучения.
Г.В. Дорофеев справедливо полагает, что «описание даже одной окрестности задачи, ситуационно полной в методическом отношении, представляет собой сложную проблему, решение которой проводится на чисто интуитивном уровне и существенно зависит от опыта учителя, от уровня его математического образования и методической подготовки» [2, c. 34–35]. Но всё же есть такие окрестности задач, описание которых вполне однозначно и совсем не трудоёмко.
Более того, можно даже сформулировать удобный в практическом отношении «алгоритм» построения таких окрестностей для достаточно широкого класса математических задач.
Речь идёт об окрестности задач, полученных путём обращения некоторой исходной задачи.
Окрестность задачи в данном понимании, по сути, есть совокупность упорядоченных и составленных в соответствии с поставленной целью задач, действующих как одно целое, взаимосвязь и взаимодействие которых приводят к достижению полноты решения школьной математической задачи в целом.
В методической литературе по математике неоднократно отмечалась развивающая ценность дополнительной работы над задачей на заключительном этапе работы с ней. Признаётся важным извлечение дополнительной информации, заключающейся в связях между величинами уже решённой задачи, которое может осуществляться различными путями, в том числе и путём её обращения.
Сущность приёма обращения задачи состоит в следующем: после решения исходной задачи составляется и решается задача, обращённая по отношению к исходной, для чего из условия исходной задачи извлекаются часть или даже все данные и включаются в её требование, а из него соответственно исключаются несколько или все найденные искомые и переводятся в её условие. После этих преобразований формулируется задача, в которой требуется найти результат, выбранный в качестве искомого, используя остальные данные, в том числе и ответ исходной задачи [7].
Задачи, получаемые таким образом из исходной, будем называть обращёнными задачами.
В том случае, когда все условия исходной задачи станут требованиями новой и, наоборот, все требования исходной задачи станут условиями новой, полученную обращённую задачу будем называть обратной по отношению к исходной.
Всю совокупность обращённых задач, полученных путём обращения из исходной задачи, будем называть окрестностью обращённых задач.
Для её систематического описания процесс обращения исходной задачи можно представить в виде следующей модели (рисунок).
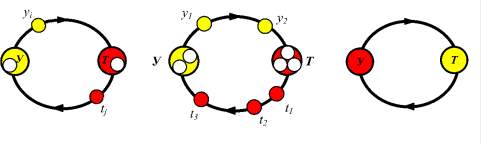
а б в
Модельное представление процесса получения окрестности обращённых задач
Если обозначить за yi совокупность элементов условия исходной задачи (У), а за tj – совокупность элементов её требования (Т), то последовательно извлекая из условия исходной задачи часть или даже все данные, и включая их в её требование, а из него соответственно переводя несколько или все найденные искомые в её условие, процесс получения окрестности обращённых задач можно представить в виде модели (рисунок).
Если, к примеру, одно данное из условия (пусть yi) исходной задачи переводится в искомые и одно найденное значение (скажем tj) – в условие, то такой способ получения обращённой задачи отражён на рисунке, а. Если же таковых элементов будет взято больше, к примеру, у1, у2, и t1, t2, t3, то схематичное представление процесса получения обращённой задачи будет несколько иным (рисунок, б). Чтобы получить всю окрестность обращённых задач, нужно перебрать все различные комбинации из элементов условия и требования прямой задачи, включая и тот самый случай, когда вся совокупность tj перейдет в условие (У), а вся совокупность yi перейдет в требование (Т) (рисунок, в).
Говоря об образовательном потенциале окрестности обращённых задач, прежде всего следует иметь в виду следующее [1, 4].
Во-первых, составление и решение обращённых задач способствует лучшему пониманию структуры математической задачи, обеспечивает более глубокое осознание тех взаимосвязей и отношений, которые свойственны задачной ситуации, позволяет школьникам как бы заглянуть внутрь структуры задачи и увидеть взаимосвязи её данных, данных и искомых и тем самым понять её математическую сущность, достигая при этом полноту решения исходной задачи.
Во-вторых, такая работа над уже решённой задачей приобщает учащихся к математическому творчеству, способствует развитию их креативности, поскольку процесс обращения адекватен процессу исследования определенной проблемы и обеспечивает формирование у школьников умений, необходимых для выполнения творческих исследовательских работ.
В-третьих, что, на наш взгляд, является исключительно важным в условиях развивающей образовательной парадигмы современной школы, ценность приёма обращения заключается в превращении прямой связи мыслей в обратную связь, что способствует развитию такого фундаментального умственного качества, как дивергентность мышления.
Раскроем на конкретных примерах методические особенности работы с окрестностью обращённых задач.
Задача 1. Катер по течению реки прошёл 87,5 км за 5 часов, а против течения это же расстояние он прошёл за 7 часов. Чему равна собственная скорость катера и скорость течения реки?
Шаг 1: решаем данную задачу 1.
Решение:
1) 87,5:5 = 17,5 км/ч – скорость катера по течению реки;
2) 87,5:7 = 12,5 км/ч – скорость катера против течения реки;
3) 17,5 – 12,5 = 5 км/ч – удвоенная скорость течения реки;
4) 5:2 = 2,5 км/ч – скорость течения реки;
5) 12,5 + 2,5 = 15 км/ч – собственная скорость катера.
Ответ: 15 км/ч; 2,5 км/ч.
Шаг 2: составляем числовую цепочку из структурных элементов решённой задачи 1.
Для того чтобы упорядочить и облегчить процесс составления новых задач, полезно после решения исходной задачи записать поэлементный состав условия и требования этой задачи в виде числовой цепочки, присоединив к нему и найденное искомое (ответ) в следующем виде:
|
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
Следуя рекомендациям П.М. Эрдниева [6], будем заключать искомое в числовой цепочке в рамочку – это позволит школьникам более наглядно увидеть исходные и искомые элементы задачи, поскольку весь поэлементный состав задачи целостно предстает перед их глазами. А это, в свою очередь, увеличивает степень осознанности учащимися возможных вариантов образования новых обращённых задач на базе исходной.
Шаг 3: составляются всевозможные числовые цепочки обращённых задач, в которых искомым элементом последовательно выступает каждый элемент данной задачи или их комбинация.
В результате последовательной реализации обращения исходной задачи числовые цепочки структурных элементов всех обращённых задач будут следующими:
|
1. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
2. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
3. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
4. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
5. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
6. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
7. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
8. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
9. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
10. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
11. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
12. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
13. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
14. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
15. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
16. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
17. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
18. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
19. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
20. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
; |
|
21. |
87,5 км |
5 ч |
7 ч |
2,5 км |
15 км/ч |
. |
Шаг 4 (1): по первой числовой цепочке, в которой в качестве искомых выбраны расстояние, пройденное катером по течению реки, и скорость течения реки, составляем текст новой обращённой задачи 1.
Прежде чем сформулировать вопрос задачи, школьникам необходимо проанализировать новые данные, связать их между собой, выяснить какие величины в принципе можно найти при таком условии, а затем уже составлять нужный вопрос. Одним из требований, предъявляемых к формулируемым задачам – это обязательная включённость всех элементов задачи в содержание её текста. Второе требование – это лаконичность вопроса. Многословные, витиеватые, трудно воспринимаемые формулировки подлежат редактированию. Если учащиеся затруднятся самостоятельно составить грамотный ряд вопросов, учитель может сам привести несколько его вариантов и предложить ученику выбрать из них наиболее подходящий и обосновать свой выбор. Затем уже целесообразно практиковать самостоятельное выдвижение вопросов учащимися.
В итоге такой деятельности может быть составлена следующая обращённая задача:
Задача 1.1. Катер по течению реки прошёл некоторое расстояние за 5 часов, а против течения реки это же расстояние – за 7 часов. Собственная скорость катера равна 15 км/ч. Найдите, какое расстояние прошёл катер по течению реки, и скорость течения реки.
Шаг 5 (1): решаем полученную задачу 1.1.
Решение:
1) 15⋅5 = 75 км – расстояние, которое прошёл катер за 5 часов;
2) 15⋅7 = 105 км – расстояние, которое прошёл катер за 7 часов;
3) 105 – 75 = 30 км – разница расстояний, пройденных катером за 5 и 7 часов;
4) 5 + 7 = 12 ч – столько времени катер был в пути;
5) 30:12 = 2,5 км/ч – скорость течения реки;
6) 15 + 2,5 = 17,5 км/ч – скорость катера по течению реки;
7) 17,5⋅5 = 87,5 км – расстояние, пройденное катером по течению и против течения реки.
Ответ: 87,5 км; 2,5 км/ч.
Как видно, объективно степень сложности обращённой задачи 1.1 не превосходит степени сложности прямой задачи 1, поскольку она содержит столько же данных, те же отношения и связи, только неизвестным выступает другой компонент этих отношений.
Итак, найдя ответ задачи 1.1 и сопоставив его с тем числом, которое заключено в рамочку в соответствующей этой обращённой задаче числовой цепочке, заключаем, что задача решена верно.
Шаг 4 (2): по второй числовой цепочке составляем и записываем текст новой задачи 1.2.
Задача 1.2. Катер по течению реки прошёл 87,5 км за несколько часов, а против течения это же расстояние он прошёл за 7 часов. Собственная скорость катера равна 15 км/ч. Найдите скорость течения реки и сколько времени шёл катер по течению реки.
Шаг 5 (2): решаем обращённую задачу 1.2.
Решение:
1) 87,5:7 = 12,5 км/ч – скорость катера против течения реки;
2) 15 – 12,5 = 2,5 км/ч – скорость течения реки;
3) 15 + 2,5 = 17,5 км/ч – скорость катера по течению реки;
4) 87,5:17,5 = 5 ч – столько времени катер шёл по течению реки.
Ответ: 2,5 км/ч; 5 ч.
Шаг 4 (3): по третьей числовой цепочке составляем и записываем текст обращённой задачи 1.3.
Задача 1.3. Катер по течению реки прошёл 87,5 км за 5 часов, а против течения он прошёл то же расстояние, но за другое время. Собственная скорость катера равна 15 км/ч. Найдите скорость течения реки и время, которое он шёл против течения реки.
Шаг 5 (3): решаем полученную задачу.
Решение:
1) 87,5:5 + 17,5 км/ч – скорость катера по течению реки;
2) 17,5 – 15 = 2,5 км/ч – скорость течения реки;
3) 15 – 2,5 = 12,5 км/ч – скорость катера против течения реки;
4) 87,5:12,5 = 7 ч – столько времени шёл катер против течения реки.
Ответ: 2,5 км/ч; 7 ч.
Шаг 4 (4): по четвёртой числовой цепочке формулируем условие и требование задачи 1.4.
Задача 1.4. Катер по течению реки прошёл некоторое расстояние за 5 часов, а против течения это же расстояние он прошёл за 7 часов. Скорость течения реки 2,5 км/ч. Найдите собственную скорость катера и расстояние, которое он прошёл по течению реки.
Шаг 5 (4): проанализируем полученную задачу.
Осуществив анализ содержания обращённой задачи 1.4, учащиеся приходят к выводу, что эта задача является неопределённой, поскольку для получения ответа на поставленный вопрос недостаточно указано данных, вследствие чего дать однозначный ответ на вопрос задачи не представляется возможным.
Отметим, что отбрасывать данную обращённую задачу 1.4 учителю не стоит, следует попытаться извлечь из неё всё возможное, потому что, даже если такая задача и не прибавит новых знаний учащимся, не окажет должного влияния на развитие их гибкости мышления, то по крайней мере она полезна тем, что поддерживает интерес учеников к процессу обращения задачи, а также способствует развитию таких качеств мышления, как логичность, критичность и др., которые, несомненно, также необходимо активно развивать у школьников в процессе их обучения и не только математике.
Шаг 6: указать, почему невозможно однозначно решить данную задачу. На данном шаге обращения задачи учитель может нацелить учащихся на указание недостающих данных, задавая вопросы следующего плана: «Почему нельзя дать ответ на вопрос задачи? Какого известного или нескольких известных не хватает? Что необходимо добавить? А можно ли что-нибудь определить даже по этим данным?».
Шаг 4 (5): по пятой числовой цепочке формулируем условие и требование задачи 1.5.
Задача 1.5. Катер по течению реки прошёл 87,5 км за несколько часов, а против течения это же расстояние – за 7 часов. Скорость течения реки равна 2,5 км/ч. Найдите собственную скорость катера и время, которое он шёл по течению реки.
Шаг 5 (5): решаем полученную задачу.
Решение:
1) 87,5:7 = 12,5 км/ч – скорость катера против течения реки;
2) 2,5⋅2 = 5 км/ч – удвоенная скорость течения реки;
3) 12,5 + 5 = 17,5 км/ч – скорость катера по течению реки;
4) 87,5:17,5 = 5 ч – время, которое потратил катер на путь по течению реки;
5) 12,5 + 2,5 = 15 км/ч – собственная скорость катера.
Ответ: 15 км/ч, 5 ч.
Аналогичным образом, осуществляя и далее данную процедуру обращения задачи 1, учащиеся могут получить следующие задачи:
Задача 1.6. Катер по течению реки прошёл 87,5 км за 5 часов, а против течения это же расстояние за другое время. Скорость течения реки 2,5 км/ч. Найдите собственную скорость катера и время, которое он потратил на путь, идя против течения реки.
Решение:
1. 87,5:5 = 17,5 км/ч – скорость катера по течению реки;
2. 17,5 – 2,5 = 15 км/ч – собственная скорость катера;
3. 15 – 2,5 = 12,5 км/ч – скорость катера против течения реки;
4. 87,5:12,5 = 7 ч – столько времени был в пути катер, плыв против течения реки.
Ответ: 15 км/ч, 7 ч.
Задача 1.7. Катер по течению реки прошёл некоторое расстояние за 5 часов, а против течения это же расстояние он прошёл за 7 часов. Скорость течения реки равна 2,5 км/ч, а собственная скорость катера 15 км/ч. Найдите расстояние, которое прошёл катер против течения реки.
Обращённая задача 1.7 является задачей с избыточными данными, благодаря чему представляется возможным осуществить её решение несколькими способами. Представим один из них.
Решение:
1) 15 – 2,5 = 12,5 км/ч – скорость катера против течения реки;
2) 12,5×7 = 87,5 км – расстояние, которое прошёл катер против течения реки.
Ответ: 87,5 км.
Задача 1.8. Катер по течению реки прошёл 87,5 км за несколько часов, а против течения это же расстояние за 7 часов. Собственная скорость катера 15 км/ч, а скорость течения реки 2,5 км/ч. Найдите время, которое катер потратил на путь по течению реки.
Решение:
1) 15 + 2,5 = 17,5 км/ч – скорость катера по течению реки;
2) 87,5:17,5 = 5 ч – время, которое был в пути катер, плыв по течению реки.
Ответ: 5 ч.
Задача 1.9. Катер по течению реки прошёл 87,5 км за 5 часов, а против течения это же расстояние он прошёл, но за другое время. Собственная скорость катера 15 км/ч, а скорость течения реки 2,5 км/ч. Найдите время, которое потратил катер на путь против течения реки.
Решение:
1) 15 – 2,5 = 12,5 км/ч – скорость катера против течения реки;
2) 87,5:12,5 = 7 ч – время, которое катер потратил на путь против течения реки.
Ответ: 7 ч.
Задача 1.10. Катер прошёл против течения некоторое расстояние за 7 часов. Собственная скорость катера равна 15 км/ч. Найдите: 1) сколько времени потребовалось бы катеру, чтобы пройти то же расстояние, но уже по течению реки; 2) скорость течения реки; 3) расстояние, пройденное катером против течения реки.
Сформулированная обращённая задача 1.10 является неразрешимой.
Очевидно и задачи 1.11–1.15 также неразрешимы.
Задача 1.16. Катер против течения реки прошёл некоторое расстояние за 7 часов, и то же самое расстояние – по течению реки. Скорость течения реки равна 2,5 км/ч, а собственная скорость катера – 15 км/ч. Найдите путь, пройденный катером по течению реки, и время, которое ему потребовалось для этого.
Решение:
1) 15 – 2,5 = 12,5 км/ч – скорость катера против течения реки;
2) 12,5⋅7 = 87,5 км – расстояние, пройденное катером против течения реки;
3) 15 + 2,5 = 17,5 км/ч – скорость катера по течению реки;
4) 87,5:17,5 = 5 ч – время, затраченное на путь по течению реки катером.
Ответ: 87,5 км; 5 ч.
Задача 1.17. Катер по течению реки прошёл 87,5 км за некоторое время, и тот же путь он прошёл против течения реки. Собственная скорость катера 15 км/ч, а скорость течения реки – 2,5 км/ч. Найдите время, которое потратил катер на путь против и по течению реки.
Решение:
1) 15 + 2,5 = 17,5 км/ч – скорость катера по течению реки;
2) 15 – 2,5 = 12,5 км/ч – скорость катера против течения реки;
3) 87,5:17,5 = 5 ч – время, потраченное катером на путь по течению реки;
4) 87,5:12,5 = 7 ч – время, потраченное катером на путь против течения реки.
Ответ: 7 ч, 5 ч.
Задача 1.18. Катер прошёл некоторое расстояние по течению реки за 5 часов, и то же самое расстояние против течения реки. Собственная скорость катера равна 15 км/ч, а скорость течения реки 2,5 км/ч. Найдите расстояние, пройденное катером по течению реки и время, потраченное на этот путь против течения реки.
Решение:
1) 15 + 2,5 = 17,5 км/ч – скорость катера по течению реки;
2) 17,5⋅5 = 87,5 км – путь, пройденный катером по течению реки;
3) 15 – 2,5 = 12,5 км/ч – скорость катера против течения реки;
4) 87,5:12,5 = 7 ч – время, потраченное катером на путь против течения реки.
Ответ: 87,5 км; 7 ч.
По структурным цепочкам 19–21 можно понять, что соответствующие им обращённые задачи невозможно будет решить, поскольку недостаточно указано данных, чтобы найти выделенные искомые.
Так, в результате обращения исходной задачи 1 получена окрестность этой задачи, состоящая из десяти разрешимых обращённых задач (1.1–1.3, 1.5, 1.6, 1.8, 1.9, 1.16–1.18), семи неразрешимых обращённых задач (1.4, 1.10–1.15, 1.19–1.21) и одной обратной задачи с избыточными данными (1.7).
Построенная в результате задачная конструкция – окрестность обращённых задач – обеспечивает полноту усвоения учащимися взаимосвязей и отношений между данными и искомыми исходной задачи, а значит, и полноту решения этой задачи. Её развивающее влияние на личность многогранно, а сам процесс создания окрестности есть путь приобщения школьников к математическому творчеству [3].
И наконец, использование обращения задач в процессе обучения математике – шаг к технологическому обновлению школьного математического образования. Это крайне актуальная задача современной методической науки, одно из перспективных направлений развития интенсивно формирующейся методической теории математических задач, позволяющее существенно усиливать развивающую значимость технологии обучения школьников математике.
Статья подготовлена по результатам научных исследований в рамках Федерального задания Минобрнауки России, регистрационный номер 01201458168, «Видовое многообразие задачных конструкций продуктивного обучения математике».
Рецензенты:
Фролов И.В., д.п.н., профессор, заведующий кафедрой физики, теории и методики обучения физике Арзамасского филиала, ФГАОУ ВПО «Нижегородский государственный университет имени Н.И. Лобачевского», г. Арзамас;
Вострокнутов И.Е., д.п.н., профессор, заведующий кафедрой информатики, теории и методики обучения информатике Арзамасского филиала, ФГАОУ ВПО «Нижегородский государственный университет имени Н.И. Лобачевского», г. Арзамас.
Работа поступила в редакцию 28.04.2014.



