Динамическую систему безопасности информации в вычислительных сетях можно представить в виде взаимовлияющих множеств: комплексов средств защиты информации (СЗИ), средств воздействия, угроз, неправомерных действий (СНД) и отношений взаимовлияния отдельных компонентов комплексов средств защиты информации и средств воздействия [5].
Будем считать, что воздействия СНД являются внешними по отношению к СЗИ, то есть будем учитывать влияние процессов системы угроз на процессы, происходящие как с СЗИ в целом, так и с их компонентами в отдельности, так и с самой защищаемой информацией. Кроме того, эти внешние воздействия могут быть постоянными или изменяться во времени.
Как отмечалось в [2], любая динамическая система (а значит, и динамическая система обеспечения безопасности информации в вычислительных сетях) может находиться в разомкнутом или замкнутом состоянии (рис. 1). Динамической системой в замкнутом состоянии является система, функционирующая с обратной связью. Динамической системой в разомкнутом состоянии – система с разорванной обратной связью. На рисунке показана точка разрыва.
На рис. 1:
– управляющие воздействия на динамическую систему с защищаемой информацией носят внешний характер и обозначаются как Y;
– возмущающие воздействия на процессы выражаются в изменении условий функционирования комплекса систем защиты информации (КСЗИ) и обозначены у(t) с индексом, соответствующим каждому процессу;
– 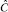 ,
, 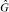 и
и 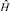 – операторы отношений между процессами, а под «возмущающим воздействием» понимается независимость параметров воздействия (угрозы) от параметров СЗИ (системы управления).
– операторы отношений между процессами, а под «возмущающим воздействием» понимается независимость параметров воздействия (угрозы) от параметров СЗИ (системы управления).
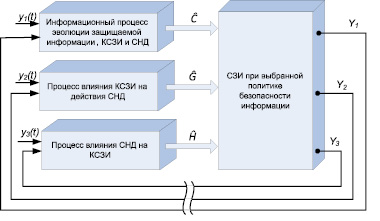
Рис. 1. Структурная схема динамической системы в замкнутом и разомкнутом состоянии
Воздействия внешних угроз на компоненты защиты или в целом на средства защиты требуют их постоянной подстройки. Если внешние угрозы не оказывают никакого воздействия на СЗИ (или их компоненты), то поведение системы защиты информации при выбранной политике безопасности (ПБ) оценивается ее устойчивостью. Устойчивость в этом случае определяется как способность поддерживать заданный режим работы по выполнению целевой функции с определенной точностью длительное (в идеале бесконечное) время вне зависимости от изменения внешних воздействий со стороны СНД. У такой СЗИ эволюция средств защиты идет впереди эволюции средств угроз, а схема динамической системы такого вида (рис. 1) подобна схеме разомкнутой системы автоматического регулирования.
Для случая, когда эволюция СЗИ отстает от эволюции угроз, схема динамической системы подобна схеме замкнутой системы автоматического регулирования (точка разрыва обратной связи на рис. 1 отсутствует). Поведение всей системы защиты информации под воздействием СНД на параметры как отдельных СЗИ, так и комплекса защиты в целом (для выбранной ПБ) также будем оценивать устойчивостью. Однако устойчивость системы в разомкнутом состоянии еще не достаточна для устойчивости замкнутого контура. Устойчивость в этом случае необходимо определять как свойство системы по поддержанию отклонений выходных параметров СЗИ относительно эталонных значений в пределах заданных малых величин. При этом именно замкнутость системы определяет особенности решения задач устойчивости эволюции процессов, происходящих в вычислительных сетях со средствами защиты, а выбранный метод оценки устойчивости дает возможность оценить такие динамические параметры эффективности СЗИ, как запас устойчивости, степень устойчивости, отклонения параметров динамической системы. Рассмотрим подробнее эти показатели.
Запас устойчивости позволяет системе СЗИ устойчиво функционировать при отклонении любого параметра этой системы в определенных пределах, то есть определяет степень удаленности параметров функционирования системы СЗИ от границы устойчивости.
Степень устойчивости характеризуется видом и скоростью возвращения переходного процесса к равновесному режиму работы системы после парирования возмущений. Причем чем значительнее степень устойчивости, тем быстрее происходит ликвидация негативных воздействий от угроз.
Параметры показателей системы при внешних угрозах определяются в соответствии с техническим заданием, в котором указываются тип решаемой задачи, формализация задачи, определяются критерии (надежность, своевременность, полнота, конфиденциальность и достоверность) для оценки показателей и т.д.
Целью исследования является анализ возможностей теоретико-множественной модели системы безопасности информации в вычислительных сетях для исследования устойчивости системы к внешним воздействиям.
Структурный элемент СЗИ при выбранной политике безопасности можно представить в таком виде, как на рис. 2. В такте n воздействие Ik(n) поступает на вход k-го блока, действие которого описывается функцией R. На этом этапе внешнее описание системы, характеризуемое состоянием
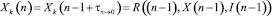 ,
,
где запись 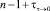 означает момент времени непосредственно после окончания n–1-го такта. Выход Ok(n) функции R получается за счет входных воздействий на нее I(n) и Х(n). В результате n-го такта значение функции состояния изменяется на
означает момент времени непосредственно после окончания n–1-го такта. Выход Ok(n) функции R получается за счет входных воздействий на нее I(n) и Х(n). В результате n-го такта значение функции состояния изменяется на 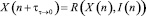 и поступает на вход этого блока в такте n + 1 в качестве Х(n + 1). Далее рассмотренный цикл повторяется на такте n + 1 и так далее для всех
и поступает на вход этого блока в такте n + 1 в качестве Х(n + 1). Далее рассмотренный цикл повторяется на такте n + 1 и так далее для всех 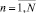 на всем временном интервале функционирования.
на всем временном интервале функционирования.
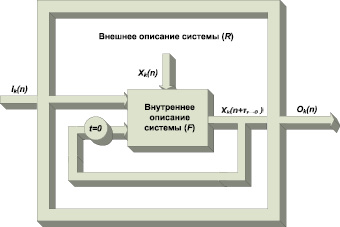
Рис. 2. Cтруктурный элемент СЗИ при выбранной политике безопасности
Разработаем структурную модель функционирования СЗИ при выбранной ПБ. Для этого будем рассматривать множество подсистем системы S = {S1, S2, ..., SN}, среди которых могут быть такие подсистемы, как конкретное средство защиты, его программное обеспечение, используемый метод защиты, защищаемая информация, отдельное внешнее воздействие при выполнении программно-технических операций и т.д. В этом множестве для каждой пары подсистем Si определим квадратную матрицу связей Мij размерностью L×L, L = mах (ni, mj) где ni, – размерность вектора Oi и mj – размерность вектора Ij. Элемент матрицы связей Мij принимает значение 1, если соответствующая составляющая (координата) вектора Oi становится составляющей (координатой) вектора Ij, в противном случае элемент матрицы равен 0. Таким образом, предполагается существование и матриц вида Мii, т.е. возможность обратной связи на элементе Si. Если же связь между Si и Si отсутствует, то Мii = 0. В случае, когда часть выходов подсистемы Si передается на входы подсистемы Sj, справедливо равенство:
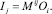 (1)
(1)
Следовательно, можно построить матрицу М размерностью N×N с элементами, в виде матриц связей:
Мij/МS = (Мij)NN .
При взаимодействии Si и Sj, 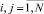 для каждой подсистемы Sj существует глобальная реакция Ri, представляющая определенное действие:
для каждой подсистемы Sj существует глобальная реакция Ri, представляющая определенное действие:
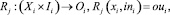 (2)
(2)
где 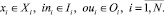
Преобразуя равенство (1) с учетом (2), получим
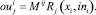 (3)
(3)
Если обозначить MijRi через Фij, то выражение (1) примет вид
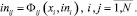 (4)
(4)
Представим сложный вектор новых значений входов по всем Si, полученный в результате воздействия сложного вектора первоначальных значений ini = (in1, ..., inN) как 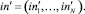 Тогда действие системы можно формализовать как
Тогда действие системы можно формализовать как
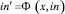 (5)
(5)
Основываясь на (5), можно отслеживать изменения входов подсистемы Si для всех in ∈ I при 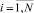 .
.
Распишем (5) с учетом временных изменений. Для этого будем считать, что вход и выход СЗИ при выбранной ПБ можно представить в виде сложных векторов, которые в каждый момент времени t > t0, t ∈ [t0, tk] принимают значения I(t) = (I1(t), ..., IN(t)) и O(t) = (O1(t), ..., ON(t)) соответственно. Следовательно, I, O и X означают множества
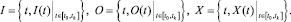 (6)
(6)
Используя выражение (5), можно записать
in(t) = Ф(x(t – t), in(t – t)), (7)
где
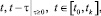
in(t) = (in1(t), in2(t), …, inN(t)) – сложный вектор входов в момент времени t;
in(t – t) = (in1(t – t), in2(t – t), …, inN(t – t)) – сложный вектор входов в момент времени t-t;
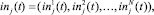
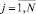 .
.
Анализ выражения (7) показывает, что значения выходного вектора системы СЗИ в момент времени t зависит от значений входного вектора в момент времени (t – t) и длительности t, где t Î [t0, tk].
При условии непрерывности действия на всем интервале времени [t0, tk] закон движения системы в векторной форме можно представить в виде интегрального уравнения:
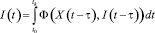 . (8)
. (8)
Далее объектом рассмотрения будет интегральное уравнение (8) в евклидовом пространстве 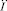 . Будем считать, что для (8) в некоторой области
. Будем считать, что для (8) в некоторой области 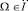 выполнены условия существования и единственности решения, а также что Ω совпадает со всем пространством
выполнены условия существования и единственности решения, а также что Ω совпадает со всем пространством 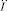 . Интересными являются решения (8), начинающиеся в момент t0. Обозначим метрику пространства
. Интересными являются решения (8), начинающиеся в момент t0. Обозначим метрику пространства 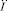 через ρ, а через
через ρ, а через 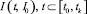 – решение (8) с начальным условием I(t0) = I0.
– решение (8) с начальным условием I(t0) = I0.
Рассмотрим классическое определение устойчивости Ляпунова и некоторые его модификации. Анализ устойчивости по Ляпунову дает ответ на вопрос о том, насколько отличается возмущенное движение системы от невозмущенного. Под невозмущенным движением понимается некоторое фиксированное решение (8), а под возмущенным – решение этого же уравнения, полученное при варьировании начальных условий.
Результаты исследования и их обсуждение
Основываясь на вышеизложенном и полученных научных результатах в работах [1, 3, 4], понятие устойчивости функционирования СЗИ при выбранной ПБ, являющееся модификацией определения устойчивости по Ляпунову [3], можно сформулировать следующим образом.
Определение 1. Решение (невозмущенное) I(t, I0) интегрального уравнения (8) устойчиво по Ляпунову, если для всякого θ > 0 существует такое δ(θ) > 0, что при любом 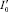 , удовлетворяющем условию
, удовлетворяющем условию 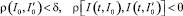 при всех
при всех 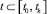 .
.
Иначе говоря, в нашем случае устойчивость по Ляпунову уравнения (8) есть равномерно непрерывная зависимость его решений на конечных интервалах времени, что выполняется для достаточно широкого класса функций [7].
Так называемая асимптотическая устойчивость помимо непрерывности требует, чтобы возмущенная траектория при t → tk стремилась к невозмущенной в смысле расстояния ρ.
Определение 2. Решение (невозмущенное) I(t, I0) интегрального уравнения (8) асимптотически устойчиво, если оно устойчиво по Ляпунову и 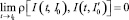 при всех
при всех 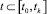 .
.
Если все решения уравнения (8) ограничены при 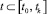 , то говорят об устойчивости по Лагранжу [3, 6], которое в этом случае при рассмотрении качественных свойств СЗИ использовать целесообразней. Для этого случая понятие устойчивости функционирования СЗИ при выбранной политике безопасности можно сформулировать следующим образом.
, то говорят об устойчивости по Лагранжу [3, 6], которое в этом случае при рассмотрении качественных свойств СЗИ использовать целесообразней. Для этого случая понятие устойчивости функционирования СЗИ при выбранной политике безопасности можно сформулировать следующим образом.
Определение 3. Система защиты информации при выбранной политике безопасности устойчива, если для любого 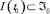 имеет место решение
имеет место решение 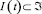 уравнения (8) для
уравнения (8) для 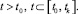
В определении: ℑ0 – множество допустимых начальных состояний защищаемой информации при выбранной политике безопасности в момент t = t0; ℑ – множество допустимых состояний защищаемой информации.
Выводы
Анализ устойчивости динамической системы безопасности на основе теоретико-множественной модели позволяет сделать следующие выводы.
В определениях 1 и 2 допускается существование достаточно малой области в пространстве возмущающих параметров, воздействующих на СЗИ при выбранной политике безопасности, при которых система будет устойчива по Ляпунову или даже асимптотически устойчива. В реальных прикладных задачах не всегда удается использовать достаточно малую окрестность возмущений. В этом случае используют понятие устойчивости по Лагранжу, которое можно интерпретировать как сохранение свойства траекторий СЗИ находиться в допустимой области пространства состояний (заданное качество СЗИ) при действии возмущений произвольной величины на начальные состояния. Как правило, множества ℑ0 и ℑ задаются на основе экспертных оценок и ограничений функционирования СЗИ при выбранной политике безопасности.
Рецензенты:
Астахова И.Ф., д.т.н., профессор кафедры математического обеспечения ЭВМ, ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж;
Дубровин А.С., д.т.н., профессор кафедры управления и информационно-технического обеспечения, ФКОУ ВПО «Воронежский институт Федеральной службы исполнения наказаний», г. Воронеж/
Работа поступила в редакцию 28.10.2014.



