Несмотря на значительные усилия, затрачиваемые на решение задач повышения качества медицинского обслуживания населения, проблема повышения уровня здоровья жителей России остается весьма далекой от своего решения. Это в значительной мере относится к герпесу, являющемуся одной из самых распространенных инфекций человека. По данным ВОЗ около 80 % населения земного шара инфицировано вирусом герпеса, смертность от вирусных инфекций, обусловленная герпесом (15,8 %), занимает второе место после гриппа. Инфицированность герпесом растет, по темпам опережая прирост населения планеты. Неконтролируемый повсеместный рост заболеваемости герпесом ставит проблему герпесвирусной инфекции в один ряд с самыми актуальными и социально значимыми проблемами здравоохранения.
Одним из способов повышения эффективности борьбы с герпесвирусной инфекцией является поиск рациональных схем лечения, эффективность которых зависит от научно обоснованной классификации клинических вариантов течения исследуемого заболевания.
С учетом этого в работе рассматриваются возможности современных математических методов для автоматической классификации различных вариантов течения одной из опасных разновидностей герпеса – генитального герпеса, которая позволит оптимизировать процесс ведения пациентов с этой патологией.
Разведочный анализ данных, привлекаемых для решения искомых классификационных задач, показал, что собираемые в лабораториях данные характеризуются высокой сложностью формализации сильно пересекающихся структур исследуемых классов.
В подобных условиях рядом исследователей рекомендуется применять аппарат нечеткой логики принятия решений
[1, 4, 5, 6, 7, 10, 12, 13, 14].
Работами кафедры биомедицинской инженерии Юго-Западного государственного университета (БМИ ЮЗГУ) показано, что выбор элементов нечетких решающих правил, их агрегацию с последующим объединением в нечеткие коллективы целесообразно осуществлять, опираясь на методологию разведочного анализа [1, 4, 7, 13].
Для решения задач синтеза нечетких решающих правил на кафедре БМИ ЮЗГУ разработан специализированный пакет прикладных программ разведочного анализа с рекомендацией выбора типов функций принадлежности и способов их агрегации в зависимости от структуры данных, характерной для определенных видов медицинских задач [5, 6, 12]. При этом было установлено, что для различных групп информативных признаков, участвующих в решении выбранной задачи наиболее подходящими (в смысле минимума ошибки классификации и профессионального понимания экспертами) являются различные типы нечетких решающих правил. Кроме того, в пространстве всех информативных признаков для различных его гиперобластей также может оказаться целесообразным использование различных типов классификационных правил.
В предлагаемой работе исследуются вопросы классификационных возможностей выбранных структур данных с синтезом нечетких решающих правил на основе моделей взаимосвязей между элементами структуры признакового пространства, полученных идентификационными алгоритмами метода группового учета аргументов (МГУА) [2, 3].
Как и в классической теории распознавания образов, на первом этапе синтеза решающих правил с участием высококвалифицированных экспертов формируется пространство информативных признаков
x1, ..., xn, которое определяется особенностями решаемой задачи, квалификацией и предпочтениями экспертов. Практика решения ряда сложных плохо формализуемых медицинских задач показала, что классификационные возможности решающих правил могут быть значительно увеличены, если использовать интегральные показатели
Y1, Y2, ..., определяемые по формуле [9]:
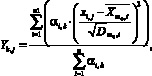 (1)
(1)
где Yk,j – j-е – значение k-го интегрального показателя; xi,j – j-е значение i-го регистрируемого показателя у пациента j, ![]() – среднее значение i-го частного показателя в базовом классе ω0;
– среднее значение i-го частного показателя в базовом классе ω0; ![]() – дисперсия i-го регистрируемого показателя крови;
– дисперсия i-го регистрируемого показателя крови;
αi,k ∈ [0, 1] – весовые коэффициенты, определяющие информационный вклад показателя xi в формирование интегрального показателя Yk.
Модели системных взаимодействий, синтезируемые алгоритмами МГУА, получают на обучающих выборках с последующей их проверкой на контрольных выборках. Причем в задачах медико-биологического профиля целесообразно объемы контрольных и обучающих выборок формировать по правилу «золотого сечения» [9].
На основании анализа различных подходов к процессам обучения классификации (распознавания образов) можно сделать вывод, что на будущее качество принятия решений влияют, с одной стороны, качественный и количественный составы обучающей выборки и, с другой стороны, качественный и количественный составы пространства информативных признаков. В свою очередь, обучающие выборки характеризуются такими показателями, как репрезентативность (принадлежность генеральной совокупности), объем и экспертное доверие. Признаковое пространство можно охарактеризовать статистическими показателями информативности, экспертным доверием к составу признаков и размерностью.
Качественные и количественные показатели, характеризующие обучающие выборки и пространство признаков, носят в основном эмпирический характер с явно выраженной нечеткостью определений. Исходя из этого, для описания используемых показателей с учетом сложившейся терминологии в области нечеткой логики принятия решений и теории уверенности для обозначения целостной характеристики обучающей выборки введем понятие меры доверия к обучающим способностям выборки (МДВ), а для обозначения классификационной возможности пространства признаков – меру доверия к признаковому пространству (МДП).
Для расчета этих показателей в работе предлагается использовать следующие две формулы:
![]() (2)
(2)
![]() (3)
(3)
где МДР – мера доверия к репрезентативности выборки; МДО – мера доверия к объему выборки; МДЭВ – мера доверия экспертов к выборке; МДИ – мера доверия к информационной ценности признакового пространства; МДЭП – мера доверия экспертов к составу признаков; МДК – мера доверия к размерности (количеству) информативных признаков; αi, βi – весовые коэффициенты, определяющие вклад указанных мер доверия в расчет МДВ и МДП соответственно.
Для определения перечисленных мер доверия могут использоваться экспертные оценки, статистические критерии Кульбака и Стьюдента, модифицированные формулы расчета объемов обучающей выборки (решение обратной задачи – по заданному объему выборки определить качество классификации как меру доверия к выборке) и т.д.
Учитывая, что составляющие МДВ и МДП дополняют друг друга в оценке классификационных возможностей медико-биологических данных, общая мера классификационного доверия к данным МДД определяется выражением
МДД = МДВ + МДП – МДП∙МДВ. (4)
Полученные значения мер МДД позволяют уточнять степень доверия к синтезируемым решающим правилам, поскольку учитывают не только работу самих классификационных правил, но и особенности тех данных, которые привлекаются для процессов обучения и контроля работы автоматизированной системы классификации.
В ходе реализации процессов обучения алгоритмы МГУА для каждого из исследуемых классов ωℓ состояний организма формируют системы математических моделей взаимосвязей между элементами признакового пространства и интегральных показателей вида
![]()
![]() (5)
(5)
![]()
где n1, n2 – количество показателей во множествах X и Y соответственно; ![]() ,
, ![]() – соответственно i-й показатель из множества
– соответственно i-й показатель из множества ![]() и k-й из множества
и k-й из множества ![]() по классам ωℓ; Aℓ, Bℓ, Cℓ – вектора настраиваемых параметров по классам ωℓ, полученные в ходе синтеза моделей типа (5);
по классам ωℓ; Aℓ, Bℓ, Cℓ – вектора настраиваемых параметров по классам ωℓ, полученные в ходе синтеза моделей типа (5); ![]() ,
, ![]() ,
, ![]() – функционалы структурных моделей в классе.
– функционалы структурных моделей в классе.
Наличие систем моделей (5) позволяет строить диагностические простые нечеткие модели классификации путем расчета расстояний между измеренными и вычисленными значениями регистрируемых показателей. Схема принятия нечетких классификационных решений с использованием моделей (5) приведена на рисунке.
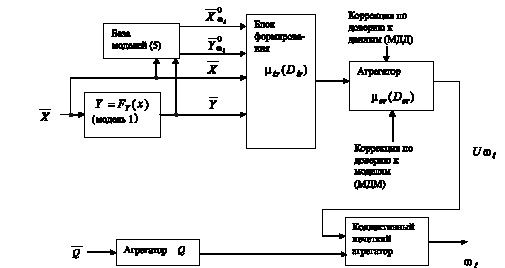
Схема алгоритма нечеткой классификации
В соответствии с этой моделью, используя расстояния между измеренными векторами ![]() и «модельными» в каждом из альтернативных классов
и «модельными» в каждом из альтернативных классов ![]() значениями исследуемых параметров, как базовые переменные для функций принадлежности к классам состояний ωℓ – μℓr(Dℓr), определяется набор r этих функций (блок формирования μℓr(Dℓr)). Агрегация данных функций позволяет синтезировать решающие правила классификации по подпространствам признаков, информативность которых по классам ωℓ обеспечивается соответствующими моделями системных взаимосвязей.
значениями исследуемых параметров, как базовые переменные для функций принадлежности к классам состояний ωℓ – μℓr(Dℓr), определяется набор r этих функций (блок формирования μℓr(Dℓr)). Агрегация данных функций позволяет синтезировать решающие правила классификации по подпространствам признаков, информативность которых по классам ωℓ обеспечивается соответствующими моделями системных взаимосвязей.
В общем случае может существовать подпространство признаков, информативность которых не определяется соответствующими моделями взаимосвязей (подгруппа признаков Q = q1, ..., qm). Относительно данного признакового Q строятся свои коллективы нечетких моделей принятия решений (агрегатор Q), которые являются составной частью финальных решающих правил (коллективный нечеткий агрегатор).
Математические модели типа (5) представляют собой приблизительное описание исследуемых классов состояний ωℓ, и поэтому они характеризуются некоторой мерой доверия к ним, которые могут быть определены коэффициентом дискриминации ![]() .
.
В соответствии с рекомендациями [2, 3] мера доверия к моделям каждого альтернативного класса в этом случае определяется выражением
![]()
Учитывая, что каждый из исследуемых классов представляется несколькими моделями, мера доверия к моделям для класса ωℓ определяется функцией
![]() (6)
(6)
По всем исследуемым классам состояний мера доверия по всем моделям (5) определяется выражением
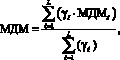 (7)
(7)
где Lr – количество уравнений (5) в классе ℓ; L – количество анализируемых классов состояний; γℓ – весовые коэффициенты, позволяющие учитывать «желаемые» доли для ошибок первого и второго рода по каждому из классов ωℓ.
При известных значениях μℓr(Dℓr), полученных в ходе обучения уверенность в классификации ωℓ по всем функциям принадлежности этого класса может быть определена выражением
![]() (8)
(8)
С учетом (4) и (7) финальная уверенность в классификации ![]() на выходе агрегатора μℓr(Dℓr) определяется выражением
на выходе агрегатора μℓr(Dℓr) определяется выражением
![]() (9)
(9)
Синтез моделей агрегатов Q и коллективного нечеткого агрегатора целесообразно выполнять, пользуясь рекомендациями [1, 4, 5, 10, 12, 13].
Экспертная оценка способов классификации вариантов протекания генитального герпеса позволила остановиться на следующей классификационной схеме:
ω1 – больные, у которых герпес клинически не обнаруживается (24 человека);
ω2 – больные с обнаруженными следами герпеса (35 человек);
ω3 – больные с обнаруженным герпесом (16 человек);
ω4 – больные с клинически наблюдаемым герпесом (49 человек);
ω5 – контрольная группа относительно здоровых людей без заболевания герпесом.
Характерной особенностью контрольной группы является то, что при отсутствии у них генитального герпеса они могут иметь заболевания со сходной симптоматикой, что может создавать картину «схожести» регистрируемых лабораторных показателей.
Разведочный анализ, проведенный в работе [9], позволил сформировать пространство информативных признаков в следующем составе:
Х1 – Т-хелперы/индукторы CD3+4+ (процент);
Х2 – Т-хелперы/индукторы CD3+4;
Х3 – незрелые Т-лимфоциты CD3+4+8+;
Х4 – подкласс цитолитических Т-лимфоцитов CD3+(16/56)+;
Х5 – иммунорегуляторный коэффициент CD4+/CD8;
Х6 – CD8+Т-лимфоциты (экспрессирующие рецепторы к IL2);
Х7 – фенопик NK-клеток CD3-16+56-(низкая);
Х8 – цитолитические CD8+ лимфоциты, содержащие перфорин;
Х9 – иммуноглобулин М;
Х10 – иммуноглобулин А;
Х11 – осаждение в 3 % ПЭГ;
Х12 – лизис эритроцитов, покрытых антителами;
Х13 – лизис интактных эритроцитов.
На репрезентативных обучающих выборках, используя алгоритмы МГУА для всех исследуемых классов состояний, были получены конкретные выражения типа (5), характеризующие внутриклассовые системные взаимосвязи:
Класс ω1:
Х8 = 93,3 – 19,51Х4;
Х9 = 312,9 – 60,8Х5.
Класс ω2:
Х9 = 142,4 + 65,9Х3.
Класс ω3:
Х13 = 25,9 + 0,263Х4.
Класс ω4:
Х5 = 1,93 – 0,012Х1;
Х1 = 34,9 + 0,584(X132/X42).
Класс ω5:
Х6 = 0,1Х2 – 65;
Х5 = 0,0455Х4 + 2,35;
Х5 = 0,0012Х2 + 0,5;
Х9 = –5 + 2X41,5;
Х1 = 0,083Х6 + 35,4;
Х8 = 12,6Х4 + 64,7;
Х3 = 0,003Х2 – 1,53;
Х2 = 813,5 + 0,142Х1∙Х6;
Х6 = 17,6 + 3,142∙10 – 5Х2∙Х3∙Х9;
![]()
![]()
![]()
Анализ результатов идентификации математических моделей, отражающих взаимосвязи между анализируемыми информативными показателями в процессе развития заболевания, показывает, что [9]:
1. Для класса ω1 специфичны линейные обратные зависимости между характеристиками X8 – X4 и X9 – X5. Т.е. в этом классе цитолитические CD8+ лимфоциты, содержащие перфорин и иммуноглобулин, снижаются по мере роста иммунорегуляционного коэффициента CD4+/CD8+. Это говорит о том, что первичная стадия заболеваемости характеризуется определенным уменьшением иммунного ответа организма на возможность развития заболевания в дальнейшем – соответствующей реакцией определенной физиологической системы, которая «готовится» для адекватного иммунного ответа.
2. Для класса ω2 специфичны связи между характеристиками – эта связь прямо пропорциональна. Т.е. увеличение концентрации незрелых Т-лимфоцитов CD+4+8 коррелирует с ростом иммуноглобулина М, что говорит о том, что начальная стадия развития заболевания герпесом отражается реакцией возбуждения формирования лимфоцитов на фоне адекватной реакции организма путем повышения иммунитета, отражаемого ростом концентрации иммунноглобулиновых показателей.
3. Для класса ω3 специфичны связи между характеристиками X13 – X4 – связь – прямо пропорциональная: рост подкласса цитолитических Т-лимфоцитов CD3+(16/56)+ коррелирует с ростом лизиса интактных эритроцитов.
4. Класс ω4 характеризуется ростом специфичных математических моделей (как линейного, так и нелинейного характеров). Т.е. наблюдается «смена» функционального состояния, характеризующаяся резким изменением «функциональных связей между элементами системы». Это позволяет, с точки зрения распознавания образов, выбрать данную группу в качестве «базовой» при дальнейшей классификации. Что касается описания полученных идентифицированных моделей, то здесь можно сделать следующие выводы:
– наблюдаются линейные регрессии – Т-хелперы/индукторы CD3+4+ (процент) и незрелые Т-лимфоциты CD3+4+8+ (отрицательная регрессия), – NK-клетки CD3-16+/56+ (положительная), иммунорегуляторный коэффициент CD4+/CD8+ (отрицательная). Это говорит о наличии стабилизирующей обратной отрицательной связи, вызывающей рост количества лимфоцитов в случае снижения иммунитета;
– наблюдается положительная линейная регрессия между подклассом цитолитических Т-лимфоцитов CD3+(16/56)+ и фенопиком NK-клеток CD3-16+56- (умеренная). Это говорит об одновременном росте количества указанных клеток в процессе иммунного ответа в рассматриваемом заболевании;
– наблюдается отрицательная линейная регрессия между иммунорегуляторным коэффициентом CD4+/CD8+ и цитолитическими CD8+ лимфоцитами, содержащий перфорин, а также с иммуноглобулином M. Это говорит о росте иммунной реакции в случае снижения концентрации лимфоцитов (их гибели, например) или уменьшении концентрации антител в процессе первичного иммунного ответа (возможно, данная «нетипичная» ситуация является особенностью заболевания – несмотря на рост количества лимфоцитов и иммуглобулина М – самого крупного из антител – иммунитет не повышается);
– нелинейные (мультипликативные) регрессионные математические модели позволяют сделать следующий вывод: значение показателя Т-хелперы/индукторы CD3+4 (процент) прямо пропорционально частному отношению квадрата количества лизис интактных эритроцитов к кубу количества цитолитических Т-лимфоцитов CD3+(16/56)+. Идентифицированная зависимость может отражать некоторый физиологический закон или закономерность и являться полезной моделью при анализе заболевания.
Это говорит о том, что синтез Т-хелперов во многом определяется квадратом отношения эритроцитов (перенос кислорода и транспорт диоксида углерода) к лимфоцитам (гуморальный иммунитет). Указанный закон формулируется следующим образом: относительная концентрация Т-хелперов/индукторов, несущих CD3+4 при заболевании герпесом, прямо пропорциональна квадрату отношения количества красных кровяных тел к белым.
Наиболее специфичными для класса ω5 являются корреляционные связи: Х2 с Х3, Х5 и Х6, а Х4 с Х5, Х8 и Х6.
Тем самым можно предположить, что показателями, характеризующими функционирование системообразующего фактора иммунной системы у людей, не болеющих герпесом (класс ω5), являются Х2 – Т-хелперы/индукторы и Х4 – подкласс цитолитических Т-лимфоцитов. Первые коррелируют с концентрациями Т-лимфоцитов и величиной иммунорегуляторного коэффициента, Вторые – с концентрацией лимфоцитов, иммуноглобулина М и величиной иммунорегуляторного коэффициента. Таким образом, можно говорить о том, что у людей, не больных герпесом, наблюдается взаимосвязь системообразующих показателей, отраженная значениями иммунорегуляторного коэффициента CD4+/CD8+ (Х5).
Математические модели, полученные самоорганизационными алгоритмами структурно-параметрической идентификации, позволяют сделать следующие выводы для «здоровых» людей (класс ω5):
1. Концентрация Т-хелперов/индукторов, несущих CD3+4, прямо пропорциональна произведению процентной доли данного показателя и концентрации СD+ Т-лимфоцитов (экспрессирующих рецепторов), которые, в отличие от B-лимфоцитов, характеризуют не столько процесс образования антител, сколько определяют эффективность врожденного иммунитета. Обращает на себя внимание фундаментальное изменение взаимосвязи «дирижера иммунитета» в классах «Здоровые» (ω5) и «Больные герпесом» (ω4): в первом случае – отражается эффективность врожденного иммунитета, во втором – отношение концентраций красных и белых кровяных тел.
2. Концентрация Т-лимфоцитов прямо пропорциональна произведению концентраций Т-хелперов/индукторов, незрелых Т-лимфоцитов и иммуноглобулина – М. Таким образом, у людей, не болеющих герпесом, стабилизирующая состояние «здоровья» функциональная система старается поддерживать необходимую реакцию в случае уменьшения концентрации незрелых Т-лимфоцитов за счет увеличения концентрации крупных антител под «контролем» «дирижера иммунитета».
3. Концентрация цитолитических CD8+лимфоцитов, содержащих перфорин, прямо пропорциональна концентрации цитолитических Т-лимфоцитов, что подчеркивает одновременное действие соответствующих саморегуляционных механизмов, характеризующихся данными показателями, направленных на поддержание статуса «здоровья».
4. Концентрация иммуноглобулина М прямо пропорциональна произведению концентрации незрелых Т-лимфоцитов, корню квадратному из значения концентрации цитолитических лимфоцитов, содержащих перфорин, и обратно пропорциональна процентному значению концентрации Т-хелперов/индукторов. Таким образом, можно говорить о том, что у здорового человека выработка антител происходит одновременно (синхронно) с выработкой лимфоцитов под «управлением» «дирижера иммунитета, что способствует поддержанию уровня «здоровья».
5. В группе «здоровые» класс ω5 наблюдается более увеличенное взаимодействие «дирижера иммунитета» – концентрации Т-хелперов/индукторов, несущих CD3+4 – чем в группе больных герпесом. Таким образом, можно сделать вывод, что ослабление работы фактора, отражающегося в значениях данного показателя иммунной системы, приводит к развитию инфекционных заболеваний – в данном случае генитального герпеса.
По полученному набору моделей самоорганизации были, в соответствии с рекомендациями [4, 6, 8, 13], синтезированы наборы функций принадлежностей μℓr(Dℓr) с их агрегацией по правилу (8). Проверка качества классификации, проведенная на репрезентативной контрольной выборке, показала, что их диагностическая эффективность не хуже 0,9, что является приемлемым для медицинской практики результатом.
Рецензенты:
Егошина И.Л., д.т.н., доцент, профессор кафедры радиотехнических и медико-биологических систем, Поволжский государственный технологический университет,
г. Йошкар-ола;
Коровин Е.Н., д.т.н., профессор кафедры системного анализа и управления в медицинских системах, Воронежский государственный технический университет, г. Воронеж.
Работа поступила в редакцию 23.10.2014.



