При распространении волн в мелководных водоемах нередко на их пути встречаются различные препятствия, такие как волноломы, пирсы, берегоукрепительные сооружения и др. В результате чего происходит деформация волны. Также немаловажным является то, что в результате постоянного воздействия волн на берегоукрепительные сооружения происходит их разрушение. И изучение волновых процессов, происходящих около надводных и полностью погруженных в жидкость тел, является важной задачей, так как моделирование данных процессов позволяет предугадать последствия этих воздействий.
В работе приведены результаты численных экспериментов моделирования распространения волны на поверхности водоема. Представлены модели, в которых объект, находящийся в жидкости, рассматривается как прямоугольник. В первом случае как объект, простирающийся от дна до поверхности жидкости, во втором, как объект, имеющий опоры, установленные на дне водоема.
Постановка волновой задачи
Требуется найти решение неоднородного волнового уравнения:
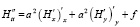 , (1)
, (1)
удовлетворяющего начальным условиям:
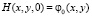 ,
,
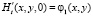 (2)
(2)
и граничным условиям:
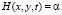 , при
, при 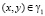 . (3)
. (3)
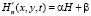 , при
, при 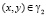 , (4)
, (4)
где a – волновое число, f – функция, описывающая распределение и интенсивность колебаний.
Аппроксимация задачи
Расчетная область вписана в прямоугольник. Покроем область равномерной прямоугольной расчетной сеткой ω = ωt×ωx×ωy:
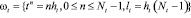 ,
,
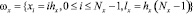 ,
,
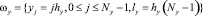 ,
,
где n, i, j – индексы по временной координате и пространственным координатным направлениям Ox, Oy соответственно, ht, hx, hy – шаги по временной координате и пространственным координатным направлениям Ox, Oy соответственно, Nt, Nx, Ny – количество узлов по временной координате и пространственным координатным направлениям Ox, Oy соответственно, lt, lx, ly – длина расчетной области по временной координате и пространственным координатным направлениям Ox, Oy соответственно.
Построим разностную схему, аппроксимирующую уравнение (1) с соответствующими граничными и начальными условиями (2)–(4). Для получения дискретной модели воспользуемся интегро-интерполяционным методом [1–3]. Проинтегрируем уравнение (1) по области Dtxy:
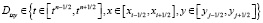 ,
,
в результате чего получим:
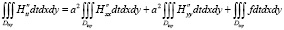 .
.
После вычисления интегралов в левой и правой части уравнения разделим полученное выражение на hx, hy, ht, в результате чего получим конечно-разностную схему аппроксимирующую задачу (1)
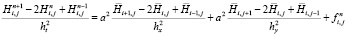 ,
,
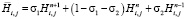 .
.
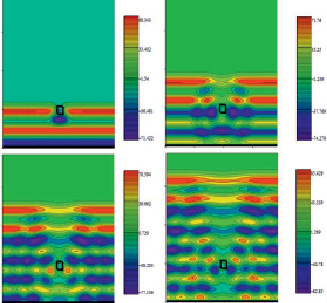
Рис. 1. Рассеяние плоской волны на прямоугольнике
Результаты численных экспериментов
На рис. 1 приведены результаты численных экспериментов по моделированию рассеяния волны на прямоугольнике.
Постановка задачи волновой
При построении двумерной математической модели движения водной среды воспользовались трехмерной гидростатической моделью [7, 14]. Исходными уравнениями гидродинамики (теории мелкой воды) являются:
– система уравнений Навье–Стокса [1–4, 8]
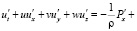
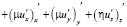 ,
,
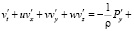
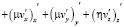 , (5)
, (5)
– уравнение неразрывности для несжимаемой жидкости
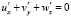 , (6)
, (6)
– уравнение гидростатики [9, 10]
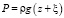 . (7)
. (7)
Система уравнений (5)–(7) рассматривается при следующих граничных условиях:
– на дне условие непроницаемости и трения [4, 14]
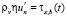 ,
,
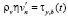 ,
,
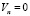 ,
,
– на поверхности задается подъем уровня и ветровые напряжения [11]
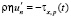 ,
,
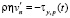 ,
,
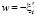 ,
,
– на боковых границах условие скольжения без трения
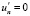 ,
, 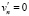 ,
, 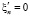 ,
,
где x – функция подъема уровня (функция возвышения), V = {u, v, w} – вектор скорости движения водной среды, P – давление, m, h – коэффициенты турбулентного обмена по горизонтальному и вертикальному направлениям соответственно, g – ускорение свободного падения, r – плотность жидкости, tx, ty – тангенциальное напряжение на дне жидкости.
Уравнение гидростатики в случае наличия на поверхности жидкости надводного тела [13]:
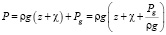 .
.
Доопределим функцию возвышения в случае наличия на поверхности жидкости надводного тела:
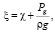
где c – функция, описывающая геометрию дна надводного тела.
Двумерная модель гидродинамики
Расчетной областью является прямоугольник. Так же, как и в случае волновой задачи, покроем область равномерной прямоугольной расчетной сеткой w = wt×wx×wy.
Уравнение неразрывности (6) в гидростатическом случае запишется в виде
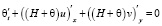 , (8)
, (8)
где 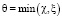 .
.
Система уравнений Навье–Стокса (5) с учетом гидростатического приближения в двумерном случае запишется в следующем виде:
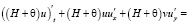
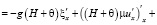
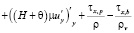 ,
,
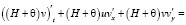
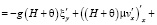
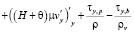 . (9)
. (9)
Схемы расщепления по физическим процессам
Рассмотрим двумерную модель движения водной среды, представленную уравнениями (8), (9). Воспользуемся схемами расщепления по физическим процессам [2, 9–12] для системы (9). При этом решение исходной задачи находится вначале на неком промежуточном временном слое:
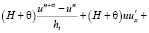
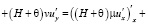
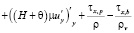 ,
,
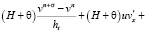
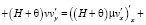
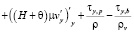 , (10)
, (10)
а затем на следующем
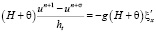 ,
,
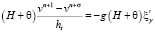 . (11)
. (11)
Для решения задачи (11) необходимо вычислить функцию возвышения уровня для этого продифференцируем первое уравнение данной системы по переменной x, второе по y и сложим их в результате чего получим:
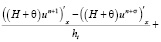
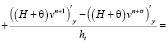
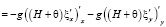 .
.
С учетом выполнения уравнения неразрывности поля скорости данное уравнение может быть записано:
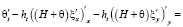
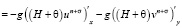 .(12)
.(12)
Уравнения системы (10)–(12) решаются в следующем порядке: вначале находим поле скорости на промежуточном временном шаге (10), затем находим функцию возвышения уровня (12) и потом уточняется поле скорости (11).
Приведены результаты численных экспериментов по моделированию распространения гидродинамических волновых процессов, которые дают возможность провести оценку воздействия волн на сооружения, имеющие опору на дне водоема (рис. 2).
Область применения – построение поля скоростей движения водной среды на сетках с высокой разрешающей способностью, учитывающих такие физические параметры, как ветровые напряжения, трение о дно, форму, амплитуду и частоту волновых колебаний, рельеф дна и учет наличия различных сооружений в мелководном водоеме.
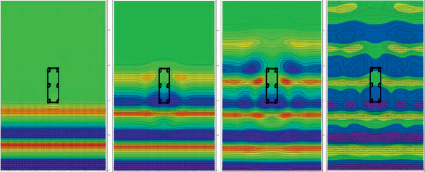
Рис. 2. Динамика изменения функции возвышения уровня
Заключение
Разработана двумерная модель волновых гидродинамических процессов, которая описывает движение водной среды как в случае наличия препятствия (сооружений, конструкций) на поверхности водоема, так и в случае его отсутствия. Из полученной системы уравнений нетрудно получить модель движения мелкой воды и двумерную модель, не учитывающую изменение геометрии водной поверхности. При моделировании плоских двумерных течений впервые использована дискретная модель, учитывающая частичную заполненность контрольных областей, отличную от нуля и единицы, для описании сложной границы раздела двух сред.
Работа выполнена при частичной поддержке проектов Программы № 43 фундаментальных исследований Президиума РАН по стратегическим направлениям развития науки «Фундаментальные проблемы математического моделирования».
Рецензенты:Илюхин А.А., д.ф.-м.н., профессор, профессор кафедры математики, Таганрогский институт имени А.П. Чехова (филиал) РИНХ, г. Таганрог;
Сухинов А.И., д.ф.-м.н., профессор, Начальник НОЦ «Комплексные исследования и математическое моделирование» НИИ многопроцессорных вычислительных систем им. А.В. Каляева, ЮФУ, г. Таганрог.
Работа поступила в редакцию 12.02.2015.



