Расчет коэффициентов запаса прочности деталей поршневых двигателей при одноосном напряженном состоянии и асимметричном цикле нагружения с амплитудой σa и средним напряжением σm проводят на основании зависимостей, предложенных С.В. Серенсеном и Р.С. Кинасошвили [4]. При действии нормальных напряжений
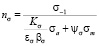, (1)
где Kσ – эффективный коэффициент концентрации напряжений; εσ – масштабный фактор; βσ – коэффициент поверхностного слоя; ψσ – коэффициент влияния асимметрии цикла или коэффициент, характеризующий чувствительность материала к асимметрии цикла [1].
При расчете на кручение для коэффициента запаса прочности используют аналогичную формулу с заменой σ на τ.
Иногда зависимость (1) называют коэффициентом выносливости при переменном нагружении, что не вполне корректно. Это было бы справедливо, если бы в знаменателе (1) стояло значение неприведенного напряжения, которое изменяется вовсе не по симметричному циклу, переменное рабочее напряжение.
Предельная амплитуда напряжений σra для лабораторного образца при асимметричном цикле нагружения может быть выражена уравнением, хорошо соответствующим экспериментальным данным в диапазоне изменения коэффициента асимметрии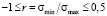 
:
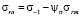, (2)
где σrm – текущее значение предельного среднего напряжения цикла.
В расчетной практике чаще для определения ψσ всего пользуются схематизированной диаграммой предельных амплитуд Серенсена-Кинасошвили
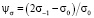, (3)
где σ0 – предел выносливости лабораторных образцов при пульсирующем цикле.
Поскольку значение σ0 в справочной литературе не приводится, то рекомендуется определять ее по приближенным формулам [7]. Для сталей при изгибе и растяжении-сжатии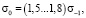 
при кручении 
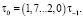Верхние пределы относятся к мягким сталям. Для чугуна 
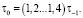Нетрудно заметить, что при таком выборе σ0 или τ0 коэффициенты ψσ и ψτ будут постоянными, не зависящими от механических характеристик материала.
В работе [4] для сталей расчет ψσ предлагается проводить по формуле
, (4)
где σв – предел прочности, МПа.
Из (3) следует, что ψσ изменяется от 0,1 при σв = 400 МПа до 0,32 при σв= =1500 МПа. При кручении принимают ψτ = 0,5 ψσ.
Между тем, значение ψσ и ψτ можно определить, построив схематизированные диаграммы предельных циклов σra = f(σrm) с использованием линейной зависимости Гудмана
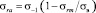, (5)
а также параболической Гербера
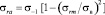. (6)
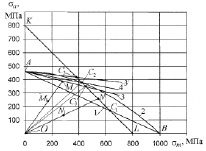
Рис. 1. Диаграмма предельных амплитуд для стали 40ХН: 1 – прямая Гудмана; 2 – парабола Гербера; 3 – предельная прямая Серенсена-Кинасошвили (σ0 = 1,6s-1); 3’ – то же при σ0 = 1,8σ-1; 4 – предлагаемая прямая схематизированной диаграммы
На рис. 1 для стали 40ХН (с характеристиками механической прочности в МПа: предел прочности σв = 1000; предел текучести σ0,2 = 800; предел выносливости при симметричном цикле σ-1 = 460) построена диаграмма предельных амплитуд с использованием зависимостей (5) – прямая 1 и зависимость (6) – кривая 2.
Для деталей из пластичных материалов зависимости (5) и (6) справедливы только на некотором участке диаграммы σra = f(σrm), так как опасным для них является не только усталостное разрушение, но и переход за предел текучести, что приводит к возникновению остаточных деформаций, искажающих форму и размеры детали. Поэтому максимальные напряжения циклов должны быть меньше не только предела выносливости, но и предела текучести σmax = σa + σm < σ0,2.
Для того, чтобы исключить из диаграммы σra = f(σrm) ту область, где предельное максимальное напряжение σrmax = σra + σrm > s0,2, проведем прямую KL, отсекающую на осях координат отрезки OL и OK, равные пределу текучести (для стали 40ХН σ0,2 = 800 МПа, рис. 1). Уравнение прямой KL имеет вид:
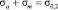. (7)
Таким образом, для деталей из пластичных материалов диаграмма предельных амплитуд в осях координат σm-σa ограничена линией 1 или параболой 2 (рис. 1) до их пересечения в точках C1 и C2 с прямой KL, а далее – прямыми C1L или C2L. Координаты точек ломаных AC1L или AC2L дают предельные значения σra и σrm в зависимости от выбранной функции σra = f(σrm).
На рис. 1 по уравнению (2) и (3) построены предельные прямые Серенсена-Кинасошвили 3 для σra (s0 = 1,6σ-1, ψσ = 0,11) и 3’ (σ0 = 1,8σ-1, ψσ = 0,25) до пересечения их с прямой KL в точках C3 и C’3 соответственно. Заметим, что предельная прямая AC’3 (если принять σ0 = 1,8σ-1) располагается выше параболы Гербера, что противоречит результатам исследований П. Форреста [3].
Для стали 40ХН, используя (4), найдем значение ψσ = 0,22. Предельная прямая, построенная по зависимости (2) с учетом (4), в этом случае почти совпадает с прямой 3’ (рис. 1).
Построим схематизированную диаграмму, используя три точки: σ0,2, σ-1 и координаты точки пересечения C2 (σrm; σa) параболы Гербера с прямой KL.
Объединим в систему зависимости (6) (парабола Гербера) и (7), после решения которой получим координаты точки C2 (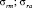
):
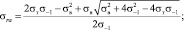(8)
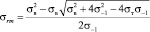. (9)
Соединив точки A и C2 (σrm; σra), получим новую схематизированную диаграмму OAC2L (рис. 1), в которой тангенс угла наклона прямой AC2 к оси абсцисс численно равен коэффициенту Ψσ, учитывающему влияние среднего напряжения (постоянной составляющей цикла) на предел выносливости:
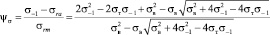. (10)
При расчете значения Ψs по формуле (10) используются только те характеристики механической прочности, которые приводятся в справочной литературе.
Формулы (8) и (9) позволяют определить, какой вид разрушения является опасным при известных рабочих средних σm и амплитудных σa напряжениях. Если при расчете деталей σm/ σa < σrm /σra , то рабочий цикл напряжений располагается в области OAC2 (рис. 1) и расчет запаса прочности следует вести по зависимости (1). Если же σm/σa > σrm /σra, то расчет ведется по зависимости [4, 1, 7]:
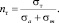(11)
Значения отношений предельных σrm /σra, а также коэффициентов ψσ, могут быть определены по формулам (8), (9) и (10) для сталей, если известны механические характеристики материалов.
В предлагаемой нами схематизированной диаграмме предельная прямая AC2 располагается между параболой 2 и прямой 1, т. е. она удовлетворяет результатам экспериментальных данных для пластичных металлов [3, 8].
В то же время, при оценке влияния среднего касательного напряжения на сопротивление усталости в [3] отмечается, что для пластичных металлов при кручении большинство экспериментальных результатов с максимальными касательными напряжениями, не превышающими предел текучести τт, располагается выше параболы Гербера (6).
Если аппроксимировать зависимость предельного амплитудного касательного напряжений τa от среднего τm по результатам экспериментальных данных эллиптической зависимостью [8]
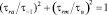, (12)
то кривая, по строенная по (12), располагается выше параболы Гербера (построенной по уравнению (6) с заменой σ на τ).
На рис. 2 для стали 40ХН (с характеристиками механической прочности для касательных напряжений в МПа: предел прочности τв = 580; предел текучести τ0,2 = 460; предел выносливости при симметричном цикле τ-1 = 270) построены диаграммы предельных амплитуд с использованием зависимостей: параболической Гербера (6)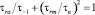 
(кривая 1) и эллиптической (12) (кривая 2).
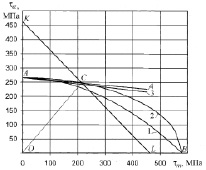
Рис. 2. Диаграмма предельных амплитуд τra = f(τrm) для стали 40ХН: 1 – парабола Гербера; 2 – эллиптическая кривая; 3 – предельная прямая Серенсена-Кинасошвили (τ0 = 1,8τ-1); 4 – предлагаемая прямая схематизированной диаграммы
Точка A на оси ординат определяет значение τ-1, а точка B на оси абсцисс – τв. Исключим из диаграммы τra = f(τrm) ту область, где предельное максимальное напряжение
τrmax = τra + τrm > τ0,2.
Для этого проведем прямую KL, отсекающую на осях координат отрезки OL и OK, равные пределу текучести τт. Уравнение прямой KL имеет вид:
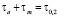. (13)
Значение Ψs,Ψτ, χσ = σrm /σra, χτ = τrm /τra легированных сталей
|
Марка стали |
Ψs |
Ψτ |
χσ = σrm /σra |
χτ = τrm /τra |
|
5ХНСД 20Х 40Х 45Х 30ХМ 35ХМ 40ХН 40ХФ 50ХФ 38ХМЮА 12ХН3А 20ХН3А 37ХН3А 18ХНВА 25ХНВА 40ХНМА 30ХГСА |
0,065…0,086 0,057…0,134 0,241…0,272 0,210…0,286 0,154…0,236 0,192…0,274 0,194…0,276 0,175…0,270 0,189…0,238 0,300…0,329 0,154…0,184 0,167…0,277 0,252…0,258 0,149…0,242 0,247 0,175…0,321 0,179…0,263 |
0,040…0,048 0,031…0,060 0,110…0,117 0,096…0,125 0,072…0,108 0,087…0,120 0,089…0,124 0,021…0,082 0,088…0,111 0,131…0,138 0,075…0,089 0,082…0,123 0,111…0,116 0,072…0,110 0,111 0,084…0,142 0,083…0,119 |
0,281…0,401 0,313…0,734 1,596…2,308 1,969…1,187 1,014…2,103 0,754…1,703 1,116…2,900 1,420…2,559 1,606…2,737 2,429…2,502 0,897…1,051 0,965…2,155 1,794…2,066 0,749…1,760 1,695 0,997…4,832 1,128…2,617 |
0,432…0,556 0,374…0,557 0,994…1,280 0,901…1,179 0,384…1,475 0,614…1,082 0,875…1,597 1,485…1,116 1,214…1,686 1,228…1,354 0,972…1,378 1,396…1,261 1,00…1,333 0,720…1,338 1,140 0,964…2,183 0,880…1,571 |
После совместного решения уравнения эллиптической кривой (12) и прямой (13) определим координаты точки С их пересечения:
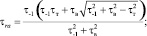(14)
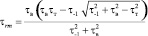. (15)
Построим схематизированную диаграмму τra = f(τrm) для касательных напряжений, соединив прямой точки A и С.
Тангенс угла наклона прямой AC (4 на рис. 2) в предлагаемой схематизированной диаграмме для касательных напряжений, численно равен коэффициенту Ψτ:
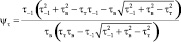. (16)
На рис. 2 прямая KL, построенная по формуле (13) при τ0,2 = 460 МПа, пересекается с эллиптической кривой 2 в точке C. На диаграмме получены две области – OAC и OCL. Если рабочие касательные напряжения τa и τm располагаются в области OAC, а τm/τa ≤ τrm/τra, то запас прочности определяется по формуле (1) с заменой σ на τ.
Если τa и τm располагаются в области OCL, то запас прочности равен
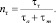(17)
В таблице приведены результаты расчетов коэффициентов yσ и yτ для сталей, которые широко используются в энергетическом машиностроении.
Рецензенты:
Кобзев А.А., д.т.н., профессор, ФГБУ ВПО «Владимирского государственного университета имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир;
Кульчицкий А.Р., д.т.н., профессор, главный специалист ООО «Завод инновационных технологий», КТЗ, г. Владимир.