В настоящее время активно развивается одно из направлений робототехники – роботы, построенные на биологических принципах, движение и конструкция которых приближены к некоторому биологическому объекту [4, 7, 8]. К таким роботам относятся ползающие гусеницеподобные, змееподобные, червеподобные, шагающие антропоморфные, плавающие роботы-рыбы, летающие роботы-насекомые, роботы-птицы, прыгающие роботы-кузнечики, роботы-кенгуру и т.д. [5, 6, 9]. По сравнению с другими типами роботов устройства, построенные на принципах бионики, копируют наиболее важные особенности биологического оригинала, что повышает их маневренность, проходимость, управляемость движения, расширяет области применения [1–3].
В работе рассматривается летающий робот, полет которого обеспечивают машущие крылья, каждое из которых состоит из двух частей, складывающихся и раскладывающихся друг относительно друга. Конструкция объекта аналогична устройству птицы, за счет взмахов крыльев изменяется их площадь и силы аэродинамического сопротивления, действующие на них со стороны окружающей среды, что позволяет им имитировать полет птиц.
Описание робота, расчетная схема
На рис. 1 приведена расчетная схема летающего робота-орнитоптера, полет которого происходит в вертикальной плоскости Охz вдоль оси Оz (вверх/вниз). Перемещение устройства вдоль своей продольной оси (от нас, на нас) либо отсутствует, либо происходит равномерно. Смещения объекта влево/вправо не наблюдается. Робот состоит из пяти звеньев 1–5, центральное 3 из которых является корпусом, а боковые 1, 2 и 4, 5 попарно образуют два крыла. Шарниры между звеньями цилиндрические, оси их вращения перпендикулярны плоскости Oxz. При такой конструкции звенья крыльев могут складываться/раскладываться как относительно корпуса, так и друг относительно друга.
При разработке математической модели будем считать, что в рассматриваемой вертикальной плоскости звенья, являющиеся крыльями, имеют вид стержней, а корпус – форму прямоугольника. Центры масс звеньев Ci совпадают с центрами их симметрии. Звенья крыльев во время полета движутся симметрично относительно вертикальной оси, являющейся осью симметрии устройства.
Полет робота происходит за счет изменения площади крыльев при их взмахах вверх и вниз. При движении крыльев вверх их звенья так складываются друг относительно друга и относительно корпуса, что проекция их площади, перпендикулярная вертикальной оси, существенно уменьшается, что приводит к уменьшению аэродинамических сил, действующих на крылья со стороны окружающей среды. Это позволяет крылу с меньшим сопротивлением подниматься вверх. При взмахе крыльев вниз их звенья занимают положение, противоположное ранее рассмотренному, т.е. крылья максимально раскладываются, тем самым увеличивая площадь перпендикулярно оси Оz, значит, и аэродинамические силы, за счет чего происходит парение устройства.
Математическая модель полета орнитоптера
Положение каждого звена пятизвенного робота на вертикальной плоскости определяется тремя координатами: проекциями xCi, yCi положения центра масс на координатные оси и углом φi поворота звена против часовой стрелки относительно оси Ох. Предложенная расчетная схема робота накладывает на его звенья связи rCi = 1.2,4,5 = f(rC3):
,
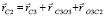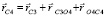, (1)
,
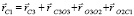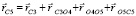. (2)
С учетом этого вектор обобщенных координат имеет следующий вид: в него входят проекции xC3, yC3 положения центра масс корпуса на оси Ох и Oz, а также углы поворота всех звеньев системы φi.
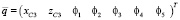. (3)
В связи с тем, что звенья 1 и 5, 2 и 4 крыльев робота во время его полета движутся с одинаковыми частотами и амплитудами, но в противоположных направлениях, справедливы соотношения: φ1 = – φ5, φ2 = – φ4. Причем такие колебания звеньев крыльев робота приводят к тому, что вращение корпуса во время полета и его смещения относительно оси Ох не будет происходить, т.е. φ3 = 0, хС3 = const. Это означает, что число обобщенных координат сокращается до трех:
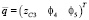. (4)
Движение орнитоптера в вертикальной плоскости происходит под действием на его звенья следующих моментов и сил: сил тяжести, приложенных к центрам масс всех звеньев и направленных вертикально вниз, моментов, создаваемых приводами и обеспечивающих сложение/разложение крыльев, а также аэродинамических сил, приложенных к центрам масс звеньев и направленных перпендикулярно векторам скоростей указанных точек.
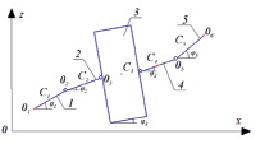
Рис. 1. Расчетная схема орнитоптера в плоскости Oхz
Рис. 2. Структурная схема системы управления орнитоптером
Аэродинамические силы вычисляются по формуле
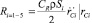(5)
где CR – безразмерный коэффициент полной аэродинамической силы, Si – эффективная площадь звена, ρ – массовая плотность воздуха,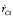 
– скорость точки Сi относительно воздуха.
Для записи системы дифференциальных уравнений, описывающих движения звеньев робота, будем использовать матричную форму записи
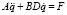, (6)
где А, B – матрицы коэффициентов, D – диагональная матрица обобщенных скоростей, F – матрица обобщенных сил.
, 
,
, 
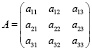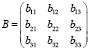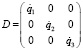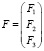. (7)
Система управления движением орнитоптера
Структурная схема системы управления приведена на рис. 2. Она включает в себя блок управления, состоящий из компаратора и регулятора, и летающего робота, состоящего из приводов и звеньев. На вход компаратора поступают фактические значения углов поворота звеньев 4 и 5 крыльев, где они сравниваются с требуемыми. Ошибки рассогласования сигналов передаются на регулятор, формирующий напряжения, подаваемые на двигатели орнитоптера, на выходе двигателей генерируются моменты, за счет которых формируются фактические углы поворота звеньев 4 и 5 крыльев, а также координаты центра масс корпуса.
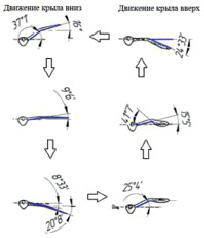
Рис. 3. Движения крыльев чайки и орнитоптера при взмахе вверх и вниз
Для обеспечения полета робота система управления должна генерировать требуемые законы изменения углов поворота звеньев 4 и 5 крыльев. В связи с тем, что исследуемый робот является бионическим, то законы движения крыльев относительно корпуса должны быть близки к аналогичным у птиц. В качестве одного из возможных вариантов в работе рассматриваются положения крыльев чайки при взмахе ими вверх и вниз (рис. 3), которые реализуются системой управления роботом [6–8]. Отметим, что амплитуды взмахов звеньев крыла, а также частота взмахов являются управляемыми параметрами.
Исследование режима зависания
Ниже представлены результаты численного моделирования движения орнитоптера в одном из режимов его движения – зависания на некоторой высоте (рис. 4, а).
Этот режим характеризуется колебаниями центра масс корпуса робота с размахом zm относительно некоторого положения равновесия zsr. В качестве параметров, влияющих на движение робота, рассматриваются амплитуда φ0 и частота ω взмахов крыльев, а также площадь звеньев крыльев и их геометрическая форма.
Положим, что крылья имеют форму пластин длинами li, ширинами bi, толщина которых близка к нулю hi > 0, а в вертикальной плоскости Oxz пластины вырождаются в стержни длинами li. Площадь каждого звена крыла равна
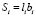, (8)
суммарная площадь звеньев крыльев вычисляется по формуле
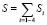. (9)
Примем допущение, что длины и ширины всех звеньев крыльев равны между собой: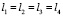 
, 
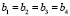. Одна и та же площадь крыльев может быть получена тремя разными комбинациями соотношений длины и ширины каждого звена крыла:
1. li > bi.
2. li = bi.
3. li < bi.
На рис. 4, б приведены графики кривых, соответствующих режиму зависания робота, при различной форме крыльев и одинаковой суммарной площади. Ниже построенных кривых находится режим посадки устройства, а выше – режим взлета. По кривым видно, что для обеспечения перехода из режима посадки в режим взлета при меньших амплитудах взмаха крыльев при одних и тех же частотах их колебаний длина каждого звена крыла должна быть больше его ширины, а для реализации того же перехода с наибольшими амплитудами колебаний крыльев, наоборот, ширина каждого звена должна быть больше его длины. С увеличением площади крыльев амплитуды их колебаний снижаются для обеспечения перехода из режима посадки в режим взлета при одной и той же частоте ω (рис. 4, в).
Режим зависания робота характеризуется размахом колебаний корпуса zm относительно некоторой высоты (положения равновесия) zsr. По кривым рис. 5, а видно, что размах колебаний корпуса плавно убывает с увеличением частоты взмахов крыльев, причем при одной и той же площади наибольший размах колебаний наблюдается при форме звеньев крыльев, когда длина больше ширины, а наименьший – когда ширина больше длины. Кривая размаха при квадратных крыльях находится между двумя вышеуказанными. По мере увеличения площади крыльев размах колебаний корпуса возрастает при малых частотах взмахов крыльев и остается неизменным при больших (рис. 5, б).
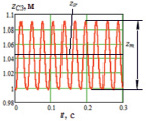
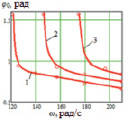
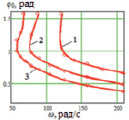
а) б) в)
Рис. 4. а – график зависимости zC3(t) в режиме зависания, б, в – графики зависимостей φ0(ω), соответствующие режиму зависания: б – при S = 0,06 м2: 1 – li > bi, 2 – li = bi, 3 – li < bi, в – при b = 0,1 м, 1 – S = 0,06 м2; 2 – S = 0,08 м2; 3 – S = 0,1 м2
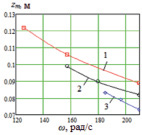
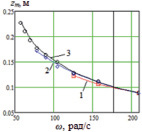
а)б)
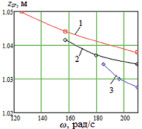
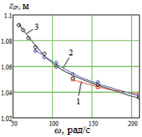
в)г)
Рис. 5. а, б – графики зависимостей zm(ω), в, г – графики зависимостей zsr(ω): а – S = 0,06 м2, 1 – l = 0,15 м, b = 0,1 м; 2 – l = b = 0,123; 3 – l = 0,1 м, b = 0,15 м; б – b = 0,1 м, 1 – S = 0,06 м2; 2 – S = 0,08 м2; 3 – S = 0,1 м2
Значение высоты, относительно которого происходят колебания корпуса, изменяется с увеличением частоты взмахов крыльев аналогично размаху, что видно по графикам рис. 5, в. Изменение высоты zsr от площади крыльев и частоты их взмахов несколько другое: при малых частотах zsr тем больше, чем больше площадь крыльев, с ростом частоты наоборот, zsr тем меньше, чем больше площадь крыльев (рис. 5, г).
Заключение
В работе рассмотрен один из режимов движения летающего робота – зависание на некоторой высоте. Робот представляет собой пятизвенный механизм, все звенья которого соединены цилиндрическими шарнирами, движение крыльев во время полета аналогично взмахам крыльев птиц, каждое крыло робота образовано двумя звеньями, складывающимися и раскладывающимися во время каждого взмаха. В результате проведенного численного моделирования установлено, что режим зависания является переходным между режимами взлета и посадки. Выявлено, что для перехода из режима посадки в режим взлета при меньших амплитудах взмахов крыльев при одной и той же частоте колебаний необходимо использовать крылья с наибольшей из возможных площадей, причем геометрически их длина должна быть как можно больше их ширины. Также определено влияние на размах колебаний корпуса по высоте и положение равновесия, относительно которого эти колебаний происходят, площади крыльев и их геометрических размеров.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-08-00787, РНФ в рамках научного проекта № 14-39-00008.