Продовольственная безопасность – неотъемлемая часть экономического благосостояния и национальной безопасности любого государства. В настоящее время рыбные ресурсы являются одним из ключевых элементов продовольственной безопасности. Увеличение потребления рыбы и ее включение в рацион питания является мощным инструментом повышения продовольственной безопасности и улучшения питания, что объясняется рядом причин: высокой биологической доступностью рыбного белка и наличием ключевых питательных микроэлементов.
Приморский край обладает одним из крупнейших в системе рыбной промышленности страны рыбохозяйственным комплексом, что обусловлено мощной сырьевой базой, геостратегическим положением края, наиболее благоприятными для бассейна климатическими условиями, наличием незамерзающих и выходящих на Транссибирскую магистраль морских рыбных портов и трудовых ресурсов [6, 7]. В сентябре 2016 г. в Приморье прошел XI Международный конгресс рыбаков. Ведущие мировые эксперты определяли стратегию развития рыбной отрасли в регионе. По информации департамента рыбного хозяйства и водных биологических ресурсов Приморья, главная тема конгресса в этом году – государственная поддержка как механизм развития рыбной отрасли. Учитывая то, что действие государственной программы Приморского края по развитию рыбохозяйственного комплекса [6] продлили до 2020 г., анализ целевых показателей данной программы является весьма актуальным.
Целью данного исследования является построение функциональной зависимости потребления рыбы и рыбопродуктов в Приморском крае от некоторых показателей рыбной отрасли. В качестве исследовательского инструментария использовались эконометрические методы [1, 9, 11]. Эконометрические методы позволяют научно обосновать стратегию и методику анализа элементов рыбной отрасли, а также прогнозировать потребление рыбопродуктов населением Приморского края и те явления, которые порождают и обусловливают исследуемый показатель. Следует отметить, что применение эконометрических методов исследования и прогнозирования используется достаточно широко, например, в работах [2–5, 8, 10].
Опираясь на доктрину продовольственной безопасности Российской Федерации [7] и государственную программу Приморского края «Развитие рыбохозяйственного комплекса в Приморском крае» [6], для исследования были выбраны следующие показатели:
y – потребление рыбы и рыбопродуктов на душу населения, кг в год,
x1 – рыба и продукты рыбные переработанные и консервированные, тыс. тонн в год,
x2 – индексы цен производителей по переработке и консервированию рыбо- и морепродуктов (в процентах, декабрь к декабрю предыдущего года),
x3 – индексы потребительских цен на рыбную продукцию (в процентах, декабрь к декабрю предыдущего года),
Таблица 2
Коэффициенты множественной детерминации
|
R2x5 |
R2x2 |
R2x6 |
R2x3 |
R2x4 |
R2x1 |
|
0,847054 |
0,764481 |
0,733864 |
0,708968 |
0,550684 |
0,497885 |
Таблица 3
Основные показатели качества модели
|
Критерий |
Фактор (исключенный) |
||||
|
– |
x5 |
x2 |
x6 |
x3 |
|
|
R2 |
0,988 |
0,987 |
0,987 |
0,984 |
0,979 |
|
F |
123,44 |
175,17 |
235,78 |
274,06 |
298,2 |
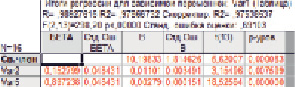
Рис. 3. Результаты множественной линейной регрессии в пакете Statistica
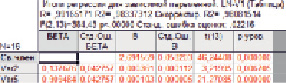
Рис. 4. Результаты множественной экспоненциальной модели в пакете Statistica
x4 – среднедушевые денежные доходы населения, рублей в месяц,
x5 – объемы экспорта рыбной продукции, тыс. тонн,
x6 – уровень использования производственных мощностей, %.
Данные анализировались за 16 лет с 2000 по 2015 гг. В качестве статистического материала использовались данные территориального органа Федеральной службы государственной статистики по Приморскому краю.
На рис. 1 представлена динамика изменения эндогенной переменной y – потребление рыбы и рыбопродуктов на душу населения, кг в год.
Первым этапом исследования является построение сквозной регрессионной модели с полным набором факторов. Результаты моделирования представлены на рис. 2.
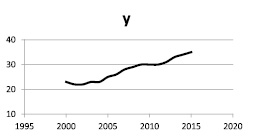
Рис. 1. Динамика потребления рыбы и рыбопродуктов на душу населения, кг в год
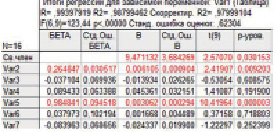
Рис. 2. Оценки множественной линейной регрессии
Таблица 1
Матрица межфакторных парных коэффициентов корреляции
|
Признак |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
1,00 |
0,24 |
0,08 |
0,35 |
0,78 |
0,09 |
|
x2 |
0,24 |
1,00 |
0,72 |
– 0,06 |
0,27 |
– 0,51 |
|
x3 |
0,08 |
0,72 |
1,00 |
– 0,30 |
– 0,09 |
– 0,56 |
|
x4 |
0,35 |
– 0,06 |
– 0,30 |
1,00 |
0,79 |
0,67 |
|
x5 |
0,78 |
0,27 |
– 0,09 |
0,79 |
1,00 |
0,28 |
|
x6 |
0,09 |
– 0,51 |
– 0,56 |
0,67 |
0,28 |
1,00 |
По результатам регрессионного анализа можно сделать вывод о качестве построенной модели в целом. Коэффициент детерминации свидетельствует о том, что уравнением регрессии объясняется почти 99 % дисперсии результативного признака, на долю остальных факторов приходится менее 2 % ее дисперсии. Критерий Фишера говорит о существенности связи между эндогенной и экзогенными переменными. Опираясь на фактические значения критерия Стьюдента и p-уровень, можно сделать вывод о незначимости и несущественности параметров при переменных x2, x3, x5, x6, что говорит о необходимости более детального исследования данных факторов. В частности, данный факт может являться косвенным признаком коллинеарности факторов. Стандартизованные регрессионные коэффициенты позволяют сравнить степень влияния каждой независимой переменной на зависимую переменную. Анализ показал, что наибольшее влияние на результативный признак оказывает переменная x4 – среднедушевые денежные доходы населения, рублей в месяц. Метод Гольдфельда – Квандта показал несостоятельность остатков для показателей x3, x6.
С целью улучшения качества модели проведены исследования данных на коллинеарность. Для оценки мультиколлинеарности факторов используется определитель матрицы межфакторной корреляции. Матрица парных коэффициентов корреляции для полного набора факторов имеет вид, представленный в табл. 1. Определитель данной матрицы равен 0,0017, что говорит о наличии мультиколлинеарности факторов.
Для обнаружения факторов, ответственных за мультиколлинеарность, были определены коэффициенты множественной детерминации, показывающие зависимость фактора xj от других факторов модели. Чем ближе значение коэффициента множественной детерминации к единице, тем больше ответственность за мультиколлинеарность фактора, выступающего в роли зависимой переменной. Сравнивая между собой коэффициенты множественной детерминации для полного набора факторов, переменные были проранжированы по степени ответственности за мультиколлинеарность (табл. 2).
Учитывая коллинеарность и степень ответственности факторов за мультиколлинеарность, на первом этапе из модели был исключен фактор x5 – объемы экспорта рыбной продукции, тыс. тонн. Вычисляя для оставшихся факторов определитель матрицы межфакторных парных коэффициентов корреляциии, оценивая качество новой регрессионной модели, приходим к выводу об уменьшении мультиколлинеарности и улучшении качества модели. Аналогичным образом поэтапно из модели были исключены факторы: x2 – индексы цен производителей по переработке и консервированию рыбо- и морепродуктов (в процентах, декабрь к декабрю предыдущего года) и x6 – уровень использования производственных мощностей, %, x3 – индексы потребительских цен на рыбную продукцию (в процентах, декабрь к декабрю предыдущего года).
На каждом этапе исключения фактора проводился расчет определителя матрицы межфакторных парных коэффициентов корреляции, строилась регрессионная модель, оценивалось качество полученной модели. Основные показатели качества моделей по мере исключения факторов (табл. 3) говорят об улучшении качества модели.
Определитель матрицы межфакторных парных коэффициентов корреляции возрастет на каждом этапе удаления факторов из модели: R1 = 0,0017, R2 = 0,109, R3 = 0,308, R4 = 0,76, тем самым подтверждается целесообразность исключения признаков-факторов из модели.
Опираясь на вышеизложенное исследование, можно предположить, что индексы потребительских цен на рыбную продукцию и индексы цен производителей по переработке и консервированию рыбо- и морепродуктов не оказывают влияния на потребление рыбы населением, так как среднегодовой темп прироста данных показателей не претерпевает существенных изменений.
Показатель «уровень использования производственных мощностей» был исключен из модели. То есть для увеличения потребления рыбы и рыбопродуктов на душу населения в Приморском крае нет необходимости наращивать производственные мощности для переработки водных биоресурсов на территории Приморского края. Их увеличение может сказаться опосредованно через увеличение среднедушевых денежных доходов населения.
Из тесной взаимосвязи фактора x5 – «объемы экспорта рыбной продукции» с факторами x4 – «среднедушевые денежные доходы населения» и x1 – «рыба и продукты рыбные переработанные и консервированные» можно предположить, что увеличение объема экспорта косвенно влияет на увеличение потребления рыбы населением.
Учитывая то, что при исключении коллинеарных факторов может быть отброшена существенная переменная, в дальнейшем будут проведены тесты на выявление пропущенных факторов, например RESET-тест Рамсея.
Результаты выявления взаимосвязи основных показателей рыбной отрасли Приморского края свидетельствуют о том, что необходимо сделать акцент на второй вариант преодоления проблем развития рыбохозяйственного комплекса Приморского края [6]. В основу этого варианта положена система мер по поддержке доходов отечественных производителей посредством развития внутреннего рынка рыбных товаров (развитие рыбоперерабатывающего кластера, аукционная торговля, развитие рыбных рынков).
Таким образом, для дальнейшего исследования и регулирования целевого показателя «потребление рыбных продуктов» на данном этапе можно работать с признаками «среднедушевые денежные доходы населения» и «производство рыбы и продуктов рыбных переработанных и консервированных».
Для моделирования взаимосвязи оставшихся показателей были построены и оценены линейная и экспоненциальная модели множественной регрессии. Оценка качества моделей проведена с помощью множественного коэффициента корреляции, коэффициента детерминации, F-критерия Фишера, t-критерия Стьюдента, доверительных интервалов параметров. Статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим был проведен анализ состоятельности оценок параметров. Для исследования остатков на гомоскедастичность использовался метод Гольдфельда – Квандта.
Результаты построения линейной модели представлены на рис. 3.
Линейная модель множественной регрессии имеет вид
y = 10,19 + 0,01x1 + 0,003x4.
По результатам моделирования сделан вывод о качестве полученной модели. F-критерий Фишера говорит о том, что полученное уравнение, в целом, статистически значимо и может быть использовано для прогноза. Доля дисперсии результативного признака составляет 97,8 %, что говорит о том, что доля дисперсии, вызванная влиянием неучтенных в модели факторов, составляет всего 2,2 %. Согласно критерию Стьюдента и доверительным интервалам для параметров, можно сделать вывод о том, что коэффициенты при оставшихся факторах значимы и надежны, то есть, на них можно опираться при построении прогноза. Метод Гольдфельда – Квандта показал гомоскедастичность остатков обоих факторных признаков. Все оценки параметров оказались состоятельными.
Результаты построения множественной экспоненциальной регрессии представлены на рис. 4.
Экспоненциальное уравнение множественной регрессии принимает вид
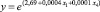 .
.
Значение F-критерия Фишера говорит о том, что полученное уравнение в целом качественное и может быть использовано для прогноза. Доля дисперсии результативного признака составляет 98,3 %. В результате оценивания параметров с помощью критерия Стьюдента и доверительных интервалов все коэффициенты оказались значимыми и надежными. Все оценки параметров оказались состоятельными. Диаграмма рассеяния между расчетными и фактическими значениями зависимой переменной показала хорошее качество подгонки диаграммы рассеяния экспоненциальной модели.
Сопоставляя стандартные ошибки построенных моделей (табл. 4) и учитывая все вышеизложенное, можно сделать вывод о том, что экспоненциальная модель множественной регрессии превосходит линейную модель по основным рассмотренным показателям.
Таблица 4
Основные показатели регрессионного анализа
|
Статистика |
Экспоненциальная модель |
Линейная модель |
|
F критерий Фишера |
384,4333 |
298,1969 |
|
p |
2,72E-12 |
1,38E-11 |
|
Стд. ош. оценки |
0,0222 |
0,691 |
Учитывая показатели качества экспоненциальной модели, приходим к выводу о возможности использования данной модели множественной регрессии для описания зависимости потребления рыбы и рыбопродуктов в Приморском крае от производства рыбной продукции и среднедушевых денежных доходов населения. Для прогнозирования экзогенных переменных, в качестве которых выступают показатели «среднедушевые денежные доходы населения» и «рыба и продукты рыбные переработанные и консервированные», будут в дальнейшем использоваться авторегрессионные модели прогнозирования (ARIMA, GARCH), модели экспоненциального сглаживания (ES) и другие модели прогнозирования временных рядов [3, 4, 10]. Выявленная зависимость может также использоваться для анализа влияния результатов проведенных мероприятий по улучшению одного из показателей рыбной отрасли Приморского края «потребление рыбы и рыбопродуктов на душу населения». Результаты, изложенные в представленной статье, являются одним из этапов исследований, связанных с изучением взаимосвязи между показателями рыбной отрасли с целью получения качественного прогноза потребления рыбы населением Приморского края и будут использованы в последующих работах авторов.



