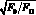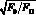При подаче воздуха стесненной струей выше рабочей зоны формируется обратный поток, который определяет параметры микроклимата в помещении. Воздухораспределение стесненными струями эффективно для помещений высотой более 4 м, таких как: производственные помещения; складские комплексы; общественные помещения, например вестибюли аэропортов.
При этом ни одна из существующих методик [3, 5, 7] не учитывает влияния видового разнообразия существующих на сегодняшний день воздухораспределительных устройств на параметры обратного потока, формируемого в рабочей зоне. Таким образом, определение зависимости скорости в обратном потоке от вида воздухораспределительного устройства является актуальной задачей.
В данной статье приведены результаты исследований методами численного эксперимента [11] течений, формирующихся в объеме помещения при подаче приточного воздуха стесненной струей выше рабочей зоны с помощью различных воздухораспределительных устройств. Для выведения искомой зависимости для скорости в обратном потоке использованы методы математического планирования эксперимента.
Материалы и методы исследования
Инструментом исследования в настоящей работе является гидродинамический вычислительный комплекс ANSYS CFX (бессрочная лицензия ООО «Арктос»), основанный на численном решении трехмерных дифференциальных уравнений сохранения [4].
Уравнения, описывающие течение в объеме рассматриваемого помещения (1)–(4), аналогичны [6].
Уравнение сохранения массы:
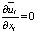 ; (1)
; (1)
– уравнение сохранения импульса:
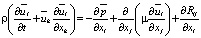 , (2)
, (2)
где 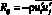 тензор Рейнольдсовых напряжений,
тензор Рейнольдсовых напряжений,
где ρ – плотность воздуха; 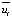 – компоненты скорости осредненного потока; t – время.
– компоненты скорости осредненного потока; t – время.
Для замыкания уравнения движения использовалась модель турбулентности: «стандартная» k-ε модель [9]:
– уравнение переноса кинетической энергии турбулентности k:
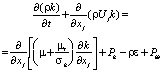 (3)
(3)
– уравнение диссипации ε кинетической энергии:
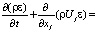
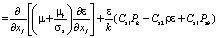 , (4)
, (4)
где k – кинетическая энергия турбулентности; ε – скорость диссипации кинетической энергии турбулентности; μt – турбулентная вязкость; Сε1 = 1,44, Сε2 = 1,92, σk = 1,σε = 1,3 – полуэмпирические коэффициенты.
Адекватность расчетов данным методом подтверждена сравнением результатов численного и натурного экспериментов [8] и [10].
1. Постановка задачи
На рис. 1 представлена геометрия помещения, используемая при проведении численного исследования.
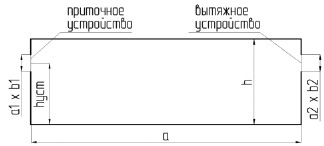
Рис. 1. Разрез помещения
Таблица 1
Параметры исследования
|
Размеры помещения a × b × h |
76 м × 8 м × 8 м |
|
Высота установки приточного устройства от пола до его центра hуст |
от 4 м до 9,95 м |
|
Размеры приточного устройства a1 × b1 |
от 100 мм × 100 мм до 1000 мм × 1000 мм |
|
Размеры вытяжного устройства a2 × b2 |
Соответствуют приточному |
|
Скорость приточного воздуха V0 |
5 м/с, 7 м/с или 10 м/с |
|
Параметр поперечного стеснения |
от 0,0125 до 0,125 |
В табл. 1 приведены основные параметры решаемой задачи.
Результаты исследования и их обсуждение
На рис. 2 представлено поле распределения компоненты скорости по оси X в поперечном сечении помещения. Плоскость поперечного сечения расположена на расстоянии 12 м от истечения в том месте, где наблюдается максимальное значение скорости в обратном потоке. Положительные значения компоненты скорости соответствуют прямому потоку, отрицательные – обратному потоку.
Результаты расчета трехмерного течения показали, что максимальные значения скорости в обратном потоке (ОП) наблюдаются в углах помещения (рис. 2). При этом максимальная скорость в углах помещения примерно на 70 % больше максимальной скорости в обратном потоке в продольной плоскости симметрии помещения (табл. 2).
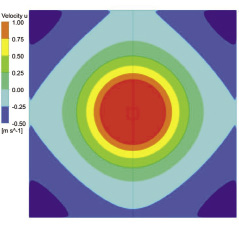
Рис. 2. Поле распределения компоненты скорости Vx в поперечном сечении помещения с максимальной скоростью в обратном потоке
Таблица 2
Максимальная скорость в обратном потоке  , м/с
, м/с
|
Скорость в обратном потоке в плоскости симметрии, м/с |
Скорость в обратном потоке в углах помещения, м/с |
|
|
Расчет по полуэмпирической формуле |
CFD-моделирование |
CFD-моделирование |
|
0,39 |
0,38 |
0,65 |
Сопоставление значений максимальных скоростей в обратном потоке под струей, полученных в результате численного моделирования и расчета по формуле 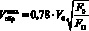 [5], применяемой для расчета в настоящее время, представлено в табл. 2. Видно, что отличие составило менее 5 %.
[5], применяемой для расчета в настоящее время, представлено в табл. 2. Видно, что отличие составило менее 5 %.
Игнорирование превышения скорости в углах помещения по отношению к скорости, полученной расчетным путем, может быть причиной существенных погрешностей в расчетах воздухораспределения при проектировании систем вентиляции и кондиционирования воздуха.
Полученный результат был подтвержден для случаев установки двух и более приточных устройств, когда максимальное значение скорости наблюдается не только в углах, но и в других областях рабочей зоны.
Таким образом, численные расчеты для подобного вида течений следует проводить в трехмерной постановке, так как расчет плоских задач может привести к некорректным результатам.
В результате исследования влияния высоты установки приточного отверстия на параметры обратного потока стесненной струи было определено, что значения максимальных скоростей в зависимости от высоты установки приточного отверстия изменяются до ≈ 20 %. Максимальное значение скорости в ОП наблюдается при установке приточного отверстия на высоте hуст = 0,75h, минимальное – при установке по центру или непосредственно под потолком.
На рис. 3 представлено изменение значений скорости в обратном потоке (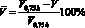 , то есть в процентах по отношению к максимальному значению) в зависимости от относительной высоты установки приточного отверстия
, то есть в процентах по отношению к максимальному значению) в зависимости от относительной высоты установки приточного отверстия 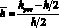 .
.
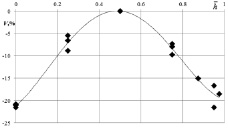
Рис. 3. Изменение скорости в обратном потоке в процентах в зависимости от относительной высоты установки
Таким образом, отсутствие учета влияния высоты установки на максимальную скорость в обратном потоке также приведет к заметным погрешностям при инженерных расчетах.
Результаты расчета течения для различного вида воздухораспределительных устройств показали наличие существенного влияния кинематического коэффициента m [5] воздухораспределителя на значение скорости в обратном потоке.
Таким образом, основной задачей исследования стало получение зависимости для определения скорости в ОП, которая учитывает вид воздухораспределительного устройства, характеризуемого кинематическим коэффициентом m. Предварительные исследования показали, что степенная зависимость в диапазоне коэффициентов m = 3,2*9,5 имеет большую погрешность, чем две линейные зависимости в диапазонах: от m = 3,2 до m = 6,7 и от m = 6,7 до m = 9,5 (значение кинематического коэффициента m = 3,2 соответствует решетке с веерным раскрытием ламелей; m = 6,7 – отверстию; m = 9,5 – соплу).
Сложность комплексного изучения течения стесненной струи воздуха, многофакторность и широкий диапазон изменения влияющих параметров вызвали необходимость применения математических методов планирования и обработки эксперимента [1] и [2]. Использование данного метода позволяет варьировать одновременно все факторы и получать количественные оценки основных эффектов и эффектов взаимодействия. А также оценить значимость того или иного фактора.
Таблица 3
Уровни варьирования факторов – Уравнение № 1
|
Наименование фактора |
Размерность |
Кодовое обозначение |
Уровни варьирования |
|
|
Нижний Xi = – 1 |
Верхний Xi = + 1 |
|||
|
Скорость, V0 |
м3/ч |
X1 |
1 |
7 |
|
Кинематический коэффициент, m |
– |
X2 |
3,2 |
6,7 |
|
Параметр стеснения, |
– |
X3 |
0,0125 |
0,125 |
Таблица 4
Уровни варьирования факторов – Уравнение № 2
|
Наименование фактора |
Размерность |
Кодовое обозначение |
Уровни варьирования |
|
|
Нижний Xi = – 1 |
Верхний Xi = + 1 |
|||
|
Скорость, V0 |
м3/ч |
X1 |
1 |
7 |
|
Кинематический коэффициент, m |
– |
X2 |
6,7 |
9,5 |
|
Параметр стеснения, |
– |
X3 |
0,0125 |
0,125 |
В табл. 3 и табл. 4 представлены уровни варьирования факторов для Уравнения № 1 и Уравнения № 2.
Основываясь на предположении о том, что искомые зависимости носят линейный характер, для построения матриц экспериментов был выбран ортогональный план первого порядка. Линейное уравнение регрессии, описывающее целевую функцию, запишется в следующем виде:
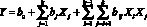 , (5)
, (5)
где k = 3- число факторов; Xi, Xj (i, j = 1, k) – кодированные значения факторов; bi, bij, – коэффициенты регрессии модели, рассчитываемые по результатам опытов.
В результате формулы для определения скорости в обратном потоке имеют вид:
– Уравнение № 1 для значений m = 3.2*6.7:
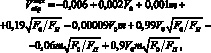 (6)
(6)
– Уравнение № 2 для значений m = 6.7*9.5:
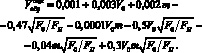 (7)
(7)
Заключение
Таким образом, проведение серии численных исследований течения стесненной струи с использованием методов математического планирования экспериментов позволило разработать методику расчета параметров формируемого ей обратного потока в зависимости от вида приточного устройства.
Полученные в результате работы зависимости следует использовать при проектировании вентиляции стесненными струями, подаваемыми выше рабочей зоны с помощью различного вида воздухораспределительных устройств.




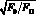 (отношение площади приточного отверстия к площади поперечного сечения помещения)
(отношение площади приточного отверстия к площади поперечного сечения помещения)