Неопределенный характер будущего обусловливает множественность будущих событий, результатов и последствий, которые наступят после принятия (или не принятия) субъектом данного решения и его реализации на практике. Каждое из событий, результатов и последствий может в будущем актуализироваться, однако, какое именно из них наступит в реальности, по какому пути пойдет развитие событий, априори неизвестно. Субъект не знает, к чему приведет принятое им решение, будет ли достигнута поставленная цель, особенно если получение результата ожидается в среднесрочной (несколько недель, месяцев) и долгосрочной перспективе (несколько лет). Неопределенность сценариев развития событий и актуализации будущих последствий и результатов является главным препятствием на пути принятия субъектом наилучшего решения [6, 8, 9]. Поэтому, прежде чем принять решение, субъекту необходимо провести прогнозирование достижения в неопределенном будущем поставленной цели и желаемого результата, а также вероятности их возможной актуализации.
Вместе с тем следует сознавать, что любой прогноз наступления будущих событий носит субъективный характер, поскольку выполняется субъектом (лицом, принимающим решение, экспертом, как индивидуальным, так и коллективным), способности которого к прогнозированию будущих событий и оценке вероятностей их наступления, весьма ограничены [3–6, 8]. И если субъект заинтересован в повышении степени актуализации запланированных результатов и достижении поставленных целей, то принимаемое решение должно опираться исключительно на научные методы прогнозирования и принятия решений [3, 5–10, 15–17], которые должны учитывать как актуальную информацию, поступающую в настоящий момент времени, так и данные, относящиеся к прогнозированию релевантных событий и их реализациям, имевшим место в прошлые периоды.
Существующие методы прогнозирования будущих событий и оценки вероятностей их наступления могут быть объединены в три группы. Методы первой группы основываются на допущении, что прошлое и будущее практически неразличимы между собой, так что тенденции, наблюдаемые в прошлом, сохраняют свой характер и в будущем. Это позволяет осуществлять прогнозирование, используя простую экстраполяцию тенденций, наблюдаемых в прошлом, на будущие периоды, при этом в качестве методов выявления тенденций за прошлые периоды выступают разнообразные регрессии, временные ряды, различные виды усреднений, скользящих средних, сглаживаний, и т.д. [2, 15]. Такая прогнозная концепция не адекватна реальности, поскольку пренебрегает неопределенностью будущего и его слабой предсказуемостью. Методы прогнозирования второй группы относятся, по преимуществу, к области финансовых и товарных рынков и используют гипотезу о стохастическом характере финансовых инструментов (курсов акций, валют, цен на сырье, энергоносители, недвижимость и пр.). Между тем данная гипотеза не подтверждается практикой [11, 12], и, более того, многочисленные исследования и факты показывают, что будущие курсы акций и валют, равно как и цены на различные виды сырья, – не являются случайными объектами, понимаемыми в смысле классической или статистической вероятностей, которые составляют предмет изучения в теории вероятностей. Так, в [11, 12] показано, что будущие цены невозможно предсказать по историческому временному ряду их изменения за прошлые периоды, причем предсказанные и наблюдаемые в реальности цены по всем видам сырья, курсам акций и валют, могут различаться между собой в несколько раз. Третья группа методов прогнозирования основывается на так называемом экспертном анализе [15], который применяется в тех случаях, когда релевантные данные по прогнозированию событий за прошлые периоды отсутствуют, или их количество недостаточно для проведения сколь-нибудь значимого анализа. При этом, как показано в [3], оценки экспертов носят субъективный характер, поскольку выполняются людьми (индивидами, или группами индивидов) и зачастую мало отличаются от оценок обычных субъектов, которые не позиционируются в качестве экспертов, иначе говоря, значимого различия между обоими видами оценок не выявляется.
Оценивание вероятностей наступления прогнозируемых событий осуществляется, как правило, одним из двух подходов – либо с использованием байесовского подхода, либо на основании гипотезы о применимости классической вероятностной модели.
Байесовский подход, основывается на следующей концепции: рассматриваются несовместные события A1, A2,…, An, образующие полную группу и именуемые гипотезами, относительно которых принято, что вероятности их наступления p(Aj) априори известны. После проведения некоего опыта, в результате которого совместно с одним из событий Ai наступает другое событие B, определяются апостериорные вероятности p(Ai|B), уточняющие априорные вероятности p(Aj) и рассчитываемые по формуле Байеса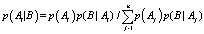 
, при этом условные вероятности p(B|Aj) также считаются известными априори. Если рассматриваются события, вероятностная модель которых может быть отнесена к типу «урны с шарами» [13], то априорные p(Aj) и апостериорные p(Ai|B) вероятности являются классическими и без труда вычисляются.
Между тем для различных сфер человеческой деятельности, в которых главным действующим лицом является человек (экономика, менеджмент, финансы и др.), вероятности наступления будущих событий p(Aj), равно как и условные вероятности p(B|Aj), не известны априори в принципе. Последние могут быть получены на основании статистических данных (при их наличии), относящихся к прогнозированию релевантных событий в прошлые периоды и в этом случае условные вероятности p(B|Aj) могут трактоваться как погрешности прогнозирования.
Необходимо понимать, что неопределенность прогнозируемого субъектом будущего обусловлена воздействием огромного множества неопределенных факторов, носящих различную природу, необратимой и непредсказуемой изменчивостью окружающей среды, самого субъекта и процесса взаимодействия субъекта со средой, окружающим социумом и пр. [8]. Следовательно комплекс условий, при котором происходит то или иное событие, является невоспроизводимым, а само событие, происходящее в будущем, – уникальным и единичным, и поэтому будущие события не являются случайными объектами [8, 13]. В этом смысле вероятности прогнозируемых событий необходимо рассматривать как субъективные вероятности, значения которых определяются субъектом, исходящим из собственного понимания ситуации.
В статье развивается метод оценивания вероятностей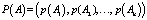 
наступления прогнозируемых событий A1, A2,…, An, который позволяет существенно уменьшить степень субъективизма при прогнозировании и оценивании вероятностей будущих событий. Показывается, что вектор вероятностей P(A) представляет собой собственный вектор полной матрицы погрешностей прогнозирования, отвечающий ее единичному собственному значению.
Оценивание вероятностей наступления прогнозируемых событий
Несмотря на то, что субъект не обладает способностью однозначно и с абсолютной точностью предсказывать какое именно событие наступит в будущем и какова будет вероятность его наступления, он тем не менее может попытаться построить множество событий, которые, по его мнению, произойдут в будущей реальности. Пусть субъект построил такое множество A с n возможными событиями A1, A2,…, An А, называемыми далее реальными событиями, образующими полную группу и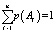 
, причем вероятности 
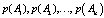априори неизвестны и подлежат определению.
Субъект составляет свой прогноз о наступлении в будущем тех или иных реальных событий A1, A2,…, An∈А на основании наблюдений над другими событиями B1, B2,…, Bn∈B, которые по его мнению, позволяют осуществить наилучший прогноз. События B1, B2,…, Bn∈B, называемые далее прогнозирующими событиями, также образуют полную группу и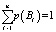 
.
Поскольку никакое событие, наблюдаемое в прошлом или в настоящем, не может однозначно и абсолютно достоверно с вероятностью единица обусловливать наступление какого-либо реального события в будущем, то прогноз субъекта о наступлении того или иного реального события Aj∈A (j = 1,2,…,n), основанный на наблюдении событий Bi∈B, (i = 1,2,…,n), не может быть достоверным в принципе. Поэтому событие Bi∈B, (i = 1,2,…,n), прогнозирующее (по мнению субъекта) наступление реального события Aj∈A, может появиться совместно с любым из событий A1, A2,…, An∈А, что можно записать как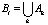 
, то есть прогноз наступления в будущем реального события Aj∈A (j = 1,2,…,n) по наблюдаемым событиям Bi∈B, (i = 1,2,…,n) всегда осуществляется с некоторой погрешностью.
Погрешность прогнозирования характеризуется двумя видами условных вероятностей p(Bi|Aj) и p(Aj|Bi), i, j = 1,2,…,n:
- p(Bi|Aj) – погрешность прогнозирования события из множества A на основании наступления прогнозирующего события Bi, в то время как на самом деле реализовалось событие Aj; она может быть определена по доступным статистическим данным прогнозирования релевантных событий в прошлые периоды, как относительное количество оправдавшихся и не оправдавшихся прогнозов;
- p(Aj|Bi) – погрешность прогноза наступления реального события Aj, который дается субъектом на основании возможного наступления прогнозирующего события Bi в настоящий момент времени. Величина погрешности прогнозирования субъекта p(Aj|Bi) отражает его субъективную убежденность в достоверности своего прогноза.
Располагая значениями погрешностей прогнозирования p(Bi|Aj), i, j = 1,2,…,n, известных из прошлого опыта, получим по формуле полной вероятности систему n равенств, определяющих полные вероятности p(Bi) наступления прогнозирующих событий Bi (i = 1,2,…,n):
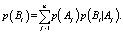(1)
Введя вектор полных вероятностей прогнозирующих событий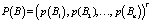 
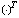– операция транспонирования), вектор искомых вероятностей прогнозируемых реальных событий 
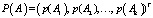, nn-матрицу погрешностей прогнозирования 
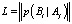релевантных событий в прошлые периоды:
,
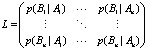равенство (1) может быть записано в матричном виде:
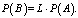(2)
Матрица L является стохастической, или марковской, векторы P(A) и P(B) – вероятностными, и обладают следующими свойствами [1, 2, 14]: (а) произведение стохастической матрицы на вероятностный вектор дает вероятностный вектор, (b) произведение двух стохастических матриц является стохастической матрицей, (c) максимальное собственное значение стохастической матрицы равно 1.
Вместе с тем, при прогнозировании событий и вероятностей их наступления, субъект ориентируется не только на данные о прогнозах релевантных событий, совершенных в прошлые периоды, но также и на новую информацию, следующую из наблюдений за событиями и тенденциями в настоящий момент времени. На основании полученной новой информации субъект строит прогноз о наступлении будущих реальных событий, основываясь на предположениях о возможном наступлении того или иного прогнозируемого реального события Aj∈A (j = 1,2,…,n), при условии реализации прогнозирующих событий Bi∈B (i = 1,2,…,n). С этой целью субъект оценивает условные вероятности p(Aj|Bi) наступления реальных событий Aj∈A (j = 1,2,…,n), при условии возможного наступления прогнозирующих событий Bi∈B (i = 1,2,…,n) в настоящий момент времени. Величина условной вероятности p(Aj|Bi), отражает, с одной стороны, степень убежденности субъекта в наступлении реальных событий Aj∈A (j = 1,2,…,n) в случае, если наступит прогнозирующее событие Bi∈B, а с другой – погрешность прогноза, которая в полной мере выявится лишь после реализации событий в будущем.
По формуле полной вероятности получаем систему n равенств определяющих вероятности p(Aj) наступления реальных событий Aj (j = 1,2,…,n):
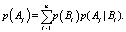(3)
Введя n∈n-матрицу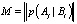 
условных вероятностей p(Aj|Bi), i, j = 1,2,…,n,
,
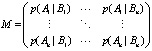систему уравнений (3) можно записть в матричном виде:
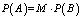. (4)
Матрица M, подобно матрице L, является стохастической и удовлетворяет условиям (a), (b) и (c), приведенным выше.
В соответствии с полученными результатами вероятности прогнозирующих P(B) и прогнозируемых реальных событий P(A), которые актуализируются в будущем, связаны между собой матричными равенствами (2) и (4). Подставляя в правую часть (4) вместо вектора P(B) его выражение из равенства (2), получим уравнение для определения искомого вектора вероятностей прогнозируемых реальных событий P(A):
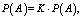(5)
где K = M•L – стохастическая n∈n-матрица (см. свойство (b)).
Из уравнения (5) следует, что искомый вектор вероятностей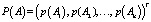 
наступления реальных событий Aj∈A, i = 1,2,…,n, представляет собой собственный вектор стохастической матрицы K = M•L, соответствующий ее единичному собственному значению. Матрица K = M•L является полной матрицей погрешностей прогнозирования и исчерпывающим образом характеризует погрешности субъекта (эксперта) при составлении прогнозов. Искомый вектор вероятностей прогнозируемых событий P(A) определяется из решения системы уравнений (5) совместно с дополнительным уравнением, описывающим условие нормировки 
.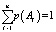