При работе дизеля в деталях, окружающих камеру сгорания (КС), возникают напряжения от действия силовой нагрузки, а также температурные напряжения, которые являются преобладающими [1]. Поэтому при расчете головки цилиндров (ГЦ) методом конечных элементов (МКЭ) необходимо учитывать действующие на неё следующие нагрузки [1]:
- максимальное давление газов в цилиндре pz на расчетном режиме (максимального крутящего момента или номинальном режиме) [2];
- усилия от затяжки шпилек (болтов) крепления головки цилиндра [3];
- давления в сечениях ГЦ от запрессовки седел и втулок клапанов (радиальные и окружные напряжения определяются в соответствии с натягами по технической документации);
- температурные напряжения, вызванные деформациями на огневом днище от перепада температур.
Цель исследования
Оценить предлагаемые критерии термоусталостной прочности, а также методы расчета с целью использования их при подготовке методики прогнозирования долговечности ГЦ поршневого двигателя.
Определение нагрузок, действующих в сечениях головки цилиндров
Максимальное давление сгорания pz определяется по результатам расчета циклов на двух режимах – номинальном и режиме максимального крутящего момента или по результатам индицирования после стендовых испытаний [4, 5]. При расчете МКЭ после разработки конечно-элементной модели (КЭМ) давление pz прикладывается к узловым точкам КЭМ на огневой поверхности ГЦ.
Усилие затяжки шпилек крепления ГЦ устанавливают из условия плотности стыка. Поскольку в технической документации устанавливается момент затяжки (момент на ключе), то усилие затяжки определяется по приближенной формуле [6]:
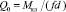 , (1)
, (1)
где Mкл – момент на ключе, Н·м; f ≈ 0,18…0,2 [6] – безразмерный коэффициент, учитывающий потери на трение в резьбе и на торце гайки; d – наружный диаметр резьбы, м.
При расчете МКЭ сосредоточенная сила Q0 заменяется распределенной нагрузкой, действующей в поперечном сечении условного полого цилиндра с наружным диаметром [6]
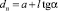 , (2)
, (2)
где a – внешний диаметр опорной поверхности гайки; l – толщина опорной поверхности головки; tgα = 0,4…0,5 (α – угол, составленный образующей конуса давления с осью) [6].
При запрессовке седел и втулок клапанов в ГЦ на опорных поверхностях ее возникает радиальное давление [7]:
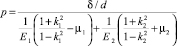 , (3)
, (3)
где δ – натяг, м; d – диаметр посадочной поверхности втулки; d1 – внутренний диаметр запрессовываемой втулки; k1 = d1/d – отношение диаметров втулки; E1, μ1 – модуль упругости и коэффициент Пуассона материала втулки соответственно; d2 – внешний диаметр охватываемой детали головки цилиндра (выбирается по толщине перемычек); k2 = d2/d; E2, μ2 – модуль упругости и коэффициент Пуассона материала ГЦ соответственно.
Обзор критериев термоусталостной прочности
Для расчета МКЭ температурных напряжений после разработки КЭМ, выбора граничных условий и решения задачи нестационарной теплопроводности определяется распределение температур в объеме ГЦ, что позволяет найти узловые значения компонентов тензора напряжений в сечениях ГЦ [8–11].
При сложном напряженном состоянии интенсивность амплитуд переменных напряжений определяется по формуле [8]:
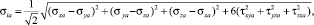 (4)
(4)
где σxa, σya, σza, τxya, τxza, τyza – амплитуды нормальных и касательных напряжений переменного цикла нагружений.
Как показали расчеты σia от температурные напряжения почти в 3,5 раза выше, чем от механического нагружения [9].
При работе поршневого двигателя в сечениях ГЦ с учетом указанных выше усилий могут возникать трещины в наиболее напряженных сечениях – в межклапанных перемычках на огневой поверхности, в перемычке между клапаном и форсуночным отверстием ГЦ и т.д.
Из детерминированной модели усталостной долговечности при нестационарном нагружении определяется суммарное число циклов 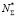 до разрушения [6]:
до разрушения [6]:
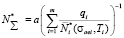 , (5)
, (5)
где m – число режимов нагружения; 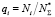 – относительная длительность i-го режим; Ni – количество циклов нагружения на произвольном i-м режиме;
– относительная длительность i-го режим; Ni – количество циклов нагружения на произвольном i-м режиме; 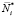 – среднее число циклов до разрушения при работе на i-м режиме;
– среднее число циклов до разрушения при работе на i-м режиме; 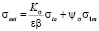 – эквивалентное напряжение; Kσ – эффективный коэффициент концентрации напряжений; ε – масштабный фактор; β – коэффициент поверхностного слоя; ψσ – коэффициент постоянных напряжений; σ1m – наибольшее постоянное напряжение цикла (первое главное напряжение); Ti – амплитуда переменных напряжений и температура на i-м режиме.
– эквивалентное напряжение; Kσ – эффективный коэффициент концентрации напряжений; ε – масштабный фактор; β – коэффициент поверхностного слоя; ψσ – коэффициент постоянных напряжений; σ1m – наибольшее постоянное напряжение цикла (первое главное напряжение); Ti – амплитуда переменных напряжений и температура на i-м режиме.
Показатель a в уравнении (5) зависит от материала ГЦ и структуры нагружения и обычно принимается в пределах a = 0,5…2. Для подтверждения зависимости (5) необходимо проведение экспериментальных исследований.
Модель (5) используется при определении многоцикловой долговечности при нестационарном нагружении.
Детерминированные модели малоцикловой долговечности рассмотрены в работе [1]. Разрушения малоцикловой усталости происходят в зонах концентрации деформаций и напряжений при упругопластических деформациях.
Как правило, если возникновение трещин в сечениях ГЦ происходит в результате циклического нагружения от действия изменяющейся температуры цикла, то оценку долговечности ГЦ нужно проводить по критериям термоусталостной прочности [1–5].
Детерминированную модель малоцикловой долговечности при нестационарном нагружении рекомендуется использовать в виде [6, 10–14]:
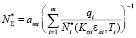 , (6)
, (6)
где 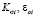 – эффективный коэффициент концентрации напряжений и амплитуда деформаций на i-м режиме; amt – показатель, зависящий от материала и структуры нагружения, деформаций и температуры на i-м режиме. Остальные обозначения приведены в зависимости (5).
– эффективный коэффициент концентрации напряжений и амплитуда деформаций на i-м режиме; amt – показатель, зависящий от материала и структуры нагружения, деформаций и температуры на i-м режиме. Остальные обозначения приведены в зависимости (5).
Как отмечено в работе [6], линейное суммирование повреждений (a ≤ 1) можно использовать при описании мягкого нагружения. В этом случае модели малоцикловой усталости совпадают с моделями усталости.
Отметим, что использовать экспериментальные данные по материалам при использовании моделей (5) и (6) необходимо с учетом следующих обстоятельств. Механические характеристики материала, полученные при термической малоцикловой усталости, отличаются от данных, полученных при механической малоцикловой усталости [13, 14].
Проверка адекватности математических моделей может быть проведена на безмоторном стенде, на котором можно уточнить граничные условия при расчетах МКЭ.
Результаты исследования и их обсуждение
Во Владимирском государственном университете на кафедре ТД и ЭУ были разработаны методики прогнозирования долговечности и ускоренных испытаний ГЦ дизеля воздушного охлаждения и стенд для ее реализации [15]. Критерием долговечности было число нагружений до появления трещин в межклапанной перемычке, а также в перемычке между клапаном и форсуночным отверстием ГЦ. Поскольку при расчетах было выявлено, что термическое нагружение больше чем в 3 раза превышает механическое нагружение, то огневая поверхность ГЦ дизеля воздушного охлаждения нагревалась галогенными лампами по определенным циклам для имитации нестационарного нагружения. Число циклов до появления трещины определенной длины фиксировалось. В ходе испытаний удалось установить, что появление трещин длиной 0,5…1 мм произошло на межклапанных перемычках после 3670…3830 циклов. Рост трещин происходил со стороны выпускного канала. Полное разрушение межклапанных перемычек произошло через 430…500 циклов после появления трещин. Долговечность головок для тракторов классов тяги 9 кН и 14 кН представлена в таблице.
Результаты испытаний ГЦ
|
Класс тяги трактора, кН |
Nв |
Nэ |
К1н |
|
9 |
401640 |
3670 |
109 |
|
14 |
314980 |
3830 |
82 |
Примечание. Nв – долговечность ГЦ вычисленная; Nэ – долговечность ГЦ, полученная в результате эксперимента на БС; К1н – коэффициент ускорения по наработке.
Полученные результаты позволили определить долговечность ГЦ за достаточно короткий срок посредством ускорения времени испытаний – в 82 раза для тракторов класса тяги 14 кН и в 109 раз для тракторов класса тяги 9 кН.
Выводы
Математическая модель прогнозирования долговечности ГЦ позволяет определить долговечность ГЦ еще на стадии проектирования, тем самым уменьшая время доводки двигателя на стадии опытных образцов. Вместе с этим, благодаря ускоренным испытаниям на безмоторном стенде, можно относительно быстро (с коэффициентом ускорения 82...109) определить время наработки на отказ, подтвердить адекватность математической модели прогнозирования надежности.



