В современных численных методах анализа динамики многотельных систем широко используется запись уравнений в форме уравнений Лагранжа I рода с неопределенными множителями [1]. С помощью уравнений такого типа решается широкий класс задач неуправляемого и управляемого движения связанной системы тел.
В робототехнике [2] при решении задач синтеза управляемого движения использование уравнений Лагранжа I рода ведет к необходимости задания программных траекторий отдельных точек системы. В работе [3] рассматривается методика встраивания в систему управления программными движениями звеньев роботов генератора устойчивых траекторий. Предложенная система управления включает в себя управляемую подсистему, уравнения генератора программных траекторий по форме, близких к прямоугольной, и уравнения голономных связей. Выбор таких траекторий был обусловлен особенностями движения схвата робота. В работах [4–6] рассматриваются генераторы автоколебательного типа, которые позволяют обеспечить устойчивость движения управляемой подсистемы по заданным траекториям.
В данной работе конструируется система управления, в которой связи генератора траекторий с объектом управления являются неголономными [7]. Приведен пример системы управления с таким типом связей и получены условия устойчивости ее решения.
Математическая модель динамики системы тел
Рассмотрим динамику многотельных систем в форме уравнений Лагранжа I рода:
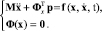(1)
где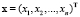 
– вектор обобщенных координат всей системы, M – матрица инерции, р – вектор множителей Лагранжа, 
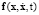– вектор внешних, внутренних сил системы, Ф – вектор геометрических связей, 
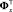– матрица переменных коэффициентов связей точек. Уравнения в форме (1) не всегда удобно использовать для численного интегрирования, поэтому второе уравнение системы часто дифференцируют два раза, после чего система принимает вид
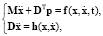(2)
где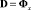 
, 
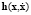– вектор правых частей уравнений связей после двукратного дифференцирования. Если движение управляемое, то система (2) дополняется вектором управления u(t) и записывается в следующей форме
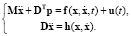
Таким образом, уравнения динамики включают в себя уравнения свободного движения тел и уравнения от геометрических связей; u(t) – вектор управляющих сил, действующих на систему.
Действие управляющих сил u(t) в уравнениях движения можно заменить уравнениями связей с заданными траекториями движения. Управление системой сводится к перемещению ее точек по заданным траекториям.
В случае неголономных связей управляемое движение системы определим следующим образом
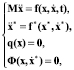(3)
где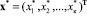 
– вектор обобщенных координат генератора системы; q(x), 
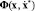– векторы связей.
После введения множителей Лагранжа система (3) запишется в виде
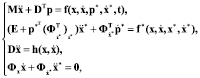
где p* – вектор множителей Лагранжа, соответствующих связям с заданными программными траекториями. При численном интегрировании такой системы дифференциальных уравнений с использованием явных методов интегрирования многократно решается система уравнений
.
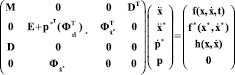Условия параметрической устойчивости системы управляемого движения
В качестве примера рассмотрим систему управляемого движения массы m: уравнения (3) будут иметь вид
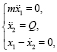(4)
после введения множителя Лагранжа –
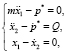(5)
где Q – постоянная сила.
Аналитическое решение системы (5) представим в виде
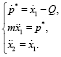
Условия связи в уравнении (4) делают зависимыми начальные условия для интегрирования уравнений (4), (5):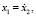 
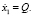
При несогласованных начальных условиях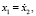 
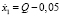возникает возмущение движения (рис. 1), что может приводить к неустойчивости численного интегрирования системы (5).
Для анализа устойчивости (5) рассмотрим линеаризованные уравнения возмущенного движения, которые в матричной форме имеют следующий вид
,
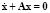где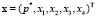 
– вектор состояния системы, A – матрица вида
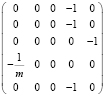. (6)
Устойчивость системы (5) определяется собственными значениями матрицы A; для матрицы (6) одно из собственных значений имеет положительную действительную часть. Возмущенная система является неустойчивой, что проявляется при несогласованных начальных условиях. Этому случаю соответствуют графики перемещения и скорости, приведенные на рис. 1.
Для обеспечения устойчивости численного интегрирования (5) умножим обе части второго уравнения системы (4) на α. В этом случае аналитическое решение системы (5) можно получить из следующего представления уравнений
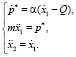(7)
Устойчивое численное решение системы (7) можно получить двумя способами:
1) возможные значения параметра α первого уравнения системы (7) положить в интервал меньший 1, т.е. α < 1.
При уменьшении α наблюдается тенденция приближения графиков к точному решению (рис. 2).
При α < 0 собственные значения матрицы (6) имеют чисто мнимые части; при 0 < α < 1 некоторые из них – положительные действительные части;
2) введение дополнительных членов пропорциональных невязкам уравнений связей. Здесь этого можно добиться путем подстановки в первое уравнение системы (7) слагаемого, пропорционального множителю Лагранжа p*. Пусть параметр α = 1, тогда решение системы (7) примет вид
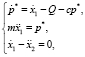
где c – положительное число.
Увеличение значений параметра c позволит стабилизировать возмущенное движение, возникающее в системе при несогласованных начальных условиях (рис. 3);
3) при получении устойчивого решения в п. 1 параметр α должен был удовлетворять условию: α < 1. Введение в первое уравнение системы (7) слагаемого – cp* снимает ограничения на значения α. Система запишется в виде
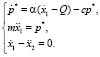(8)
Матрице A линеаризованной системы в этом случае соответствуют отрицательные и положительные действительные части собственных значений. При достаточно больших значениях α положительная действительная часть будет стремиться к нулю.
Результаты численного интегрирования таких систем представлены на рис. 4, 5.
Для устойчивого решения росту α должен сопутствовать еще больший рост c.
Собственные значения матрицы A только при α < 0 имеют нулевые и отрицательные действительные части.
При малых отрицательных значениях c: –1 < c < 0, также можно получить устойчивое решение системы (8) при условии α < 1.
Таким образом, для стабилизации системы (8) должно выполняться одно из следующих соотношений на параметры
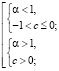
При α = 1, c = 0 система устойчива только при согласованных начальных условиях.
Рассмотрим систему (4), заменив в нем второе уравнение:
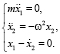(9)
Система (9) в связанном виде записывается в форме
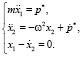
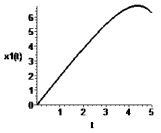
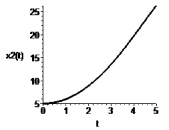
Рис. 1. Зависимость переменных x1 и x2 от времени t до стабилизации
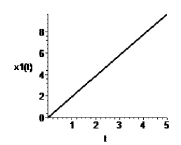
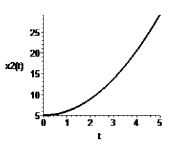
Рис. 2. Зависимость переменных x1 и x2 от времени t при α = 0,1, α ≤ –1
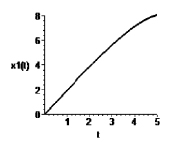
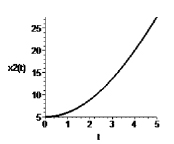
Рис. 3. Зависимость переменных x1 и x2 от времени t при c = 0,5
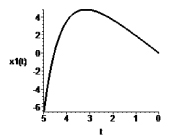
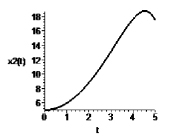
Рис. 4. Зависимость переменных x1 и x2 от времени t при α = 3, c = 1
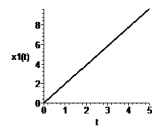
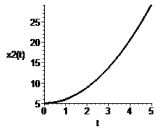
Рис. 5. Зависимость переменных x1 и x2 от времени t при α = 3, c = 30
Аналитическое решение системы (9) после дифференцирования уравнения связи представим следующим образом:
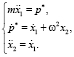(10)
Хотя система (9) имеет очевидное решение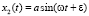 
, 
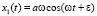, численное интегрирование уравнения (10) не дает искомого решения и поиск методов стабилизации решения требует дополнительного исследования.
Заключение
Построена система управления, в которой взаимодействие генератора программных траекторий с управляемой подсистемой обеспечивают уравнения неголономных связей.
В робототехнике зачастую требуется получить циклические движения различной формы, обеспечивающие устойчивость движения как отдельного звена, так и всей системы.
Обычно в этом случае используются робастные ПИД-регуляторы, которые не всегда могут обеспечить устойчивость системы. Поэтому проблема синтеза устойчивых режимов управления движением по заданным траекториям остается актуальной.