Сольватация (для водных растворов гидратация) – одно из определяющих явлений в растворах электролитов, ответственное практически за все их свойства. На сегодняшний день различными методами анализа открыты многие закономерности, связывающие изменение какого-либо физического свойства с определенным параметром сольватации [1–3]. Большое количество работ посвящены разработке методов определения или расчета важного параметра сольватации – числа сольватации [4, 5]. Известны несколько теоретических моделей строения растворов, обзор и анализ которых приведен в [6]. Однако следует признать, что все эти модели основаны на различных приближениях, содержащих ряд эмпирических параметров, физический смысл которых часто носит формальный характер. Они не способны охватить и описать все известные проявления сольватации, зачастую применимы либо в относительно узком интервале концентраций и температур, либо для описания отдельных систем. Поэтому поиск сколько-нибудь общих закономерностей, даже полуколичественных, связывающих явление сольватации с микроскопическими параметрами растворенного вещества или растворителя, по-прежнему остается актуальной задачей.
Цель данной работы – попытаться в рамках молекулярно-динамической теории растворов О.Я. Самойлова получить полуэмпирическое уравнение для описания чисел сольватации электролитов Z в разбавленных водных и неводных растворах, провести анализ этого уравнения и сопоставить полученные выводы с экспериментальными данными о числах сольватации электролитов Z, которые были рассчитаны по данным о динамической вязкости растворов методом, предложенным авторами в работе [7].
Теория. Основные формулы
При исследовании микроскопического механизма образования сольватов принципиально, является ли взаимодействие иона с молекулами растворителя ион-дипольным или же преобладает механизм образования ковалентной связи между молекулами растворителя и ионом. Это существенно только при положительной сольватации в первой координационной сфере иона, уже во второй координационной сфере следует учитывать только классическое электростатическое взаимодействие. В дальнейшем будет использовано это приближение.
Полная энергия молекулы растворителя в ионном растворе W может быть представлена как
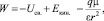 (1)
(1)
где Uсв. – энергия межмолекулярного взаимодействия молекул растворителя; Екин. – кинетическая энергия теплового движения молекул растворителя, равная Екин. 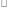 kT; k – константа Больцмана; Т – абсолютная температура;
kT; k – константа Больцмана; Т – абсолютная температура; 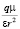 – энергия ион-дипольного взаимодействия; q – заряд иона; ε – диэлектрическая постоянная растворителя; r – расстояние между ионом и молекулой растворителя; μ – дипольный момент молекулы растворителя.
– энергия ион-дипольного взаимодействия; q – заряд иона; ε – диэлектрическая постоянная растворителя; r – расстояние между ионом и молекулой растворителя; μ – дипольный момент молекулы растворителя.
В соответствии с тем, какой из трех энергетических вкладов преобладает в уравнении (1) при данном значении r, строение раствора определяется именно этим фактором. Если преобладает вклад Uсв., то расположение молекул растворителя подобно строению кристалла (у воды это льдоподобная структура). Если преобладающей оказывается энергия ион-дипольного взаимодействия, то молекулы растворителя выстраиваются так, чтобы направление их дипольных моментов совпадало с вектором напряженности электрического поля иона. Будем называть такое упорядоченное построение молекул растворителя вблизи иона сольватной структурой. Наконец, если энергия теплового движения существенно превышает все другие члены в уравнении (1), то любое упорядочение отсутствует, молекулы растворителя распределены в растворе хаотично.
Определим радиус сольватации r0 как такое максимальное расстояние, при котором r < r0, и энергия ион-дипольного взаимодействия превышает абсолютное значение суммы двух других вкладов в общую энергию молекулы в уравнении (1):
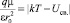 , (2)
, (2)
тогда
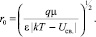 (3)
(3)
Очевидно, что при Uсв. = 0 радиус сольватации есть радиус Онзагера
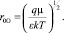 (4)
(4)
Выражение (3), таким образом, представляет собою обобщенный радиус Онзагера. Разумеется, уравнение (3) неприменимо вблизи температуры 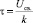 . При
. При 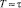 предлагаемая в данной работе качественная модель должна быть существенно уточнена учетом флуктуации параметров порядка.
предлагаемая в данной работе качественная модель должна быть существенно уточнена учетом флуктуации параметров порядка.
Как в уравнении (3), так и в уравнении (4), вообще говоря, нужно ввести полное значение дипольного момента
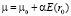 , (5)
, (5)
где α – поляризуемость молекулы растворителя; μ0 – жесткий дипольный момент молекулы растворителя; Е – напряженность электрического поля, создаваемого ионом в точке r0, равная
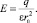 (6)
(6)
Кроме того, следует учесть также то обстоятельство, что значение ε выражается через α и μ0 по уравнению Клаузиуса – Мосотти – Дебая:
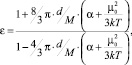 (7)
(7)
где d – плотность растворителя; М – молярная масса растворителя.
С учетом уравнений (5) и (6), уравнение (3) приобретает следующий вид:
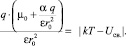 (8)
(8)
Тогда для r0 получаем уравнение
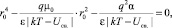
в окончательном виде
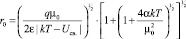 , (9)
, (9)
если Uсв. << kT, то
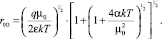 (10)
(10)
Если поляризуемость α мала, то уравнения (9) и (10) сводятся, естественно, к уравнениям (3) и (4). Если собственный дипольный момент молекулы растворителя μ0 мал и в выражении (8) им можно пренебречь, а поляризуемость α значительна, то уравнение (9) будет иметь следующий вид:
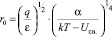 (11)
(11)
и радиус Онзагера (при Uсв. = 0)
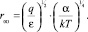 (12)
(12)
Исходя из сделанных выше определений, перейдем к математическому выражению для чисел сольватации Z. Представим объем сольватированной оболочки иона как
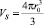 , (13)
, (13)
а количество молекул растворителя, входящих в сольватную оболочку иона (число сольватации) Z с учетом уравнения (3) в виде
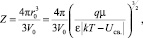 (14)
(14)
где V0 – объем, приходящийся на одну молекулу растворителя.
В случае структурированной жидкости, например воды при температурах, близких к комнатной температуре, ионы, как известно, могут локализоваться либо в позиции «замещения» молекулы растворителя, либо в позиции «внедрения» в межмолекулярные пустоты [1, 2]. При любом характере локализации размеры соответствующего иона нужно соотнести с характерным эффективным радиусом ρ того пространства в структуре растворителя, которое занимает ион (размерами пустот в случае замещения или размерами молекул растворителя в случае внедрения). Для случая воды крупные ионы (размер иона больше ρ) разрушают структуру растворителя – межмолекулярные связи вблизи внедрившегося иона разрываются или, по крайней мере, ослабляются. Подобное происходит в кристалле вблизи крупного внедренного атома: связи в кристалле-матрице оказываются растянутыми, и в ряде моделей это хорошо описывается упругими напряжениями [8]. Если радиус иона меньше, чем ρ, то структура и межмолекулярные связи растворителя также нарушаются, молекулы «стягиваются» к маленькому иону, нарушая связи между собой. Только если радиус иона в точности совпадает с ρ, то напряжения и разрыва связей не происходит. Логично предположить, что размеры области, где межмолекулярные связи растворителя нарушены за счет объемных эффектов при внедрении ионов в структуру растворителя увеличиваются с ростом различий в объеме 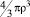 и объеме внедренных ионов. Поскольку обычно корректно не удается разделить вклад в сольватацию от каждого из ионов электролита, и реально в эксперименте определяется брутто-значение Z для электролита KmAn в целом, то объем растворителя Vd, нарушенный введением m катионов с радиусом rк и n анионов с радиусом ra равен
и объеме внедренных ионов. Поскольку обычно корректно не удается разделить вклад в сольватацию от каждого из ионов электролита, и реально в эксперименте определяется брутто-значение Z для электролита KmAn в целом, то объем растворителя Vd, нарушенный введением m катионов с радиусом rк и n анионов с радиусом ra равен
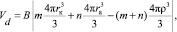 (15)
(15)
где B – константа.
Ясно, что если размеры введенных ионов совпадают с ρ, то Vd = 0. Введение модуля разности в уравнение (15) учитывает то обстоятельство, что как очень малые, так и очень крупные ионы разрушают структуру растворителя. Если область сольватного упорядочения VS простирается дальше от иона, чем область «геометрически» разрушенной структуры жидкости Vd (т.е. VS > Vd), то имеет место положительная сольватация. При обратном неравенстве VS < Vd, когда структура растворителя разрушена на расстоянии большем чем то, на котором проявляется сольватное упорядочение, имеет место отрицательная сольватация по Самойлову.
Введем определение полной эффективной величины числа сольватации Z в структурированном растворителе, как разности между числом молекул, попадающих в обобщенную сферу Онзагера, и количеством молекул в области вблизи иона с разрушенной системой межмолекулярных связей растворителя:
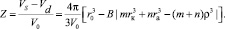 (16)
(16)
С учетом уравнения (3)
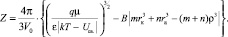 (17)
(17)
Очевидно, что при VS > Vd число гидратации Z будет больше нуля, а в случае VS < Vd – меньше нуля.
Особо следует остановиться на случае очень больших значений r0 в структурированных жидкостях. В проведенных выше оценках не учитывался тот факт, что характерные размеры D льдоподобных структурных областей в жидкой воде, например, ограничены. За пределами такой области жидкость неупорядочена. Если r0 < D, то граница гидратного упорядочения проходит в пределах структурного кластера воды. Имеет место конкуренция двух типов упорядочения, что и отражается в обобщенном радиусе Онзагера. Если же r0 > D, то граница гидратного упорядочения проходит в области, где льдоподобная структура уже отсутствует. Поскольку с ростом температуры значение D(T) уменьшается, размер гидратного образования при больших r0 и Z определяется конкуренцией гидратного упорядочения уже не с межмолекулярными связями, а с энергией тепловых колебаний. При больших Z это соответствует случаю Uсв. = 0.
Сопоставление значений 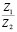 с величиной
с величиной 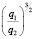 (водные растворы)
(водные растворы)
|
Электролит (1): электролит (2) |
|
|
Электролит (1): электролит (2) |
|
|
|
|
2,6 |
2,8 |
|
1,3 |
1 |
|
|
2,7 |
2,8 |
|
1,7 |
1 |
|
|
2,6 |
2,8 |
|
0,97 |
1 |
|
|
2,5 |
2,8 |
|
1,1 |
1 |
|
|
2,8 |
2,8 |
|
1,4 |
1 |
|
|
2,9 |
2,8 |
|
1,3 |
1 |
|
|
3,0 |
2,8 |
|
1,7 |
1 |
|
|
2,9 |
2,8 |
|
1,1 |
1 |
|
|
2,4 |
2,8 |
|
1,4 |
1 |
|
|
4,0 |
5,2 |
|
1,4 |
1 |
|
|
1,5 |
1,8 |
|
1,7 |
1 |
|
|
1,4 |
1,8 |
|
0,99 |
1 |
|
|
1,4 |
1,8 |
|
1 |
1 |
|
|
1,5 |
1,8 |
|
1,4 |
1 |
|
|
2,0 |
1,8 |
|
1,2 |
1 |
|
|
2,0 |
1,8 |
|
1,2 |
1 |
|
|
2,3 |
1,8 |
|
1,3 |
1 |
|
|
0,99 |
1 |
|
1,2 |
1 |
|
|
0,96 |
1 |
|
1,2 |
1 |
|
|
I,1 |
1 |
|
1,2 |
1 |
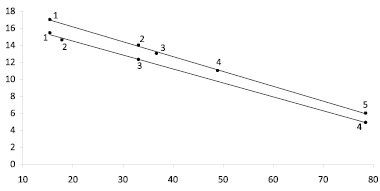
Рис. 1. Зависимость чисел сольватации Z от диэлектрической постоянной растворителя ε при 273 К: а – LiCl в изопентаноле (1), метаноле (2), N,N-диметилформамиде (3), диметилсульфоксиде (4), воде (5); б – LiNO3 в изопентаноле (1), бутаноле (2), метаноле (3), воде (4)
Результаты исследования и их обсуждение
Проведем анализ уравнения (17) и сопоставим полученные выводы с экспериментальными данными о числах сольватации электролитов Z, которые были рассчитаны по данным о динамической вязкости растворов методом, предложенным авторами в работе [7]. Определяемые этим методом числа сольватации представляют собой среднестатистическую величину, суммарно отражающую сольватацию катиона и аниона.
Зависимость чисел сольватации Z от заряда ионов. Из уравнения (17) следует, что Z должно расти при увеличении заряда ионов. При больших значениях Z, когда вторым членом в уравнении (17) можно пренебречь, появляется возможность количественной проверки. Действительно, в этом случае для двух солей
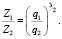
Эта зависимость неизменна, как в случае полярных растворителей, так и в случае неполярных, но поляризуемых. В таблице приведены сопоставления, полученных значений 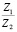 с величиной
с величиной 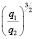 для водных растворов.
для водных растворов.
Соответствие следует признать хорошим. Для неводных растворов имеет место аналогичная закономерность.
Зависимость Z от диэлектрической постоянной растворителя. В соответствии с уравнением (17) с ростом диэлектрической постоянной растворителя ε величина Z должна уменьшаться, что действительно, имеет место (рис. 1).
Зависимость чисел сольватации от радиуса иона. Существование отрицательной гидратации и то, что граница между положительной и отрицательной гидратацией находится между ионами Na+ и K+, давно общепризнано. Впервые это было показано в работе [1], а затем подтверждено различными методами [2, 4, 5, 9, 10]. Было установлено критическое значение радиуса катиона, при котором отрицательная гидратация переходит в положительную, при 293 К оно равно 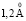 [1], при 298 К –
[1], при 298 К – 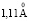 [1, 6, 9], для однозарядных анионов
[1, 6, 9], для однозарядных анионов 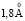 [6].
[6].
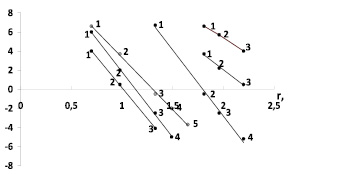
Рис. 2. Зависимость Z от радиуса ионов при 293 К: а – LiI(1), NaI(2), KI(3); б – LiBr(1), NaBr(2), KBr(3), RbBr(4); в – LiCl(1), NaCl(2), KCl(3), RbCl(4), CsCl(5); г – KF(1), KCl(2), KBr(3), KI(4); д – NaCl(1), NaBr(2), NaI(3); е – LiCl(1), LiBr(2), LiI(3)
Рассмотрим, насколько адекватно уравнение (17) позволяет оценить зависимость чисел сольватации от размера ионов и определить значение критических радиусов катиона 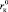 и аниона
и аниона 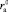 , при которых положительная гидратация переходит в отрицательную. Из уравнения (17) следует, что значения Z могут принимать как положительные, так и отрицательные значения. Из условия Z = 0 можно определить
, при которых положительная гидратация переходит в отрицательную. Из уравнения (17) следует, что значения Z могут принимать как положительные, так и отрицательные значения. Из условия Z = 0 можно определить 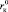 и
и 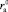 .
.
Для катиона
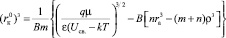 , (18)
, (18)
аналогично для аниона
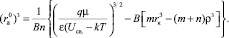 (19)
(19)
Из уравнений (18) и (19) следует, что величина 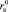 должна уменьшаться с ростом размера аниона
должна уменьшаться с ростом размера аниона 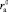
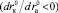 , а
, а 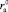 – с ростом размера катиона
– с ростом размера катиона 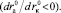
График зависимости величин Z различных электролитов от кристаллографических радиусов катионов и анионов (по Полингу) действительно демонстрирует переход от положительной к отрицательной гидратации при увеличении как радиуса катиона, так и радиуса аниона (рис. 2).
На рис. 2, а–в, представлены зависимости Z от радиуса катионов, которые подтверждают, что граница между положительной и отрицательной гидратациями действительно находится между катионами Na+ и K+, зависит от природы аниона (чем больше радиус аниона, тем меньше 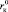 ) и приходится на критический радиус катиона
) и приходится на критический радиус катиона 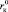 (
(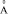 ), равный для хлоридов 1,27, нитратов 1,21, бромидов 1,1, иодидов 1,07, что совпадает с данными работ [1, 6, 9].
), равный для хлоридов 1,27, нитратов 1,21, бромидов 1,1, иодидов 1,07, что совпадает с данными работ [1, 6, 9].
Для нахождения критического радиуса аниона, к сожалению, недостаточно данных, есть только данные зависимости Z от радиуса анионов для хлоридов, бромидов, иодидов лития, натрия и калия (рис. 2, д–е). Видно, что переход от положительной гидратации к отрицательной имеет место только для галогенидов калия, лежит между ионами фтора и хлора и происходит при 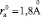 , что согласуется с данными работ Г.А. Крестова [6]. Следует полагать, для галогенидов рубидия и цезия критическое значение радиуса аниона будет меньше.
, что согласуется с данными работ Г.А. Крестова [6]. Следует полагать, для галогенидов рубидия и цезия критическое значение радиуса аниона будет меньше.
Выводы
Предложено полуэмпирическое уравнение (17) для описания чисел сольватации электролитов в водных и неводных растворителях. Проведена апробация этого уравнения, показавшая, что уравнение адекватно описывает положительную и отрицательную сольватацию в разбавленных растворах, подтверждает наличие критического радиуса катиона и аниона, при которых происходит переход от положительной сольватации к отрицательной, позволяет прогнозировать зависимость чисел сольватации от заряда и размера ионов, диэлектрической постоянной растворителя. Полученные результаты полностью согласуются с положениями теории сольватации О.Я. Самойлова, демонстрируют не только валидность предложенного полуэмпирического уравнения, но и надежность вискозиметрического метода определения Z.




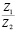
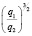
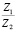
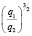
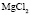 :
: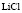
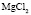 :
: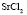
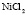 :
: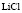
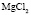 :
: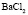
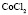 :
: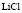
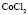 :
:
 :
:
 :
: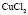
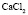 :
: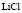
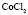 :
:
 :LiBr
:LiBr :
:
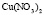 :
: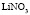
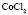 :
: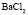
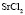
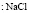
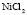 :
: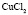
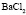
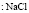
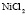 :
: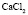
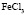 :LiCl
:LiCl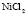 :
: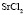
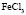 :
:
 :
:
 :
:
 :
:
 :
: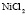
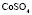 :
: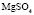
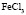 :
:
 :
:
 :
:
 :
:
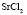
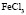 :
: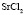
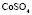 :
: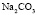
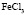 :
: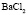
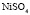 :
: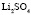
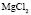 :
: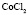
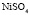 :
: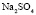
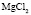 :
: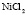
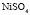 :
:
 :
:
 :
: