В последнее время начали широко применяться актуарные исследования в анализе рисков. Существует большое количество моделей, и одной из них является стохастическая модель Уилки. Такие модели описывают случайные процессы, и их «случайность» описывается при помощи теории вероятности. Немаловажную роль в их построении также играет и статистическое моделирование. В основе регулирования страховых отношений между страховщиком и страхователем лежат методы, опирающиеся на математические и статистические закономерности. Они и называются актуарными расчетами.
Большинство популярных приложений используют принцип, использующий марковские процессы при моделировании условий поведения системы. Это задачи с начальными статистическими данными, например задачи системам массового обслуживания: почта, мастерские, заправочные станции, магазины и т.д. Так, для представления состояния страхователя используется тот же подход.
В результате математического анализа получаем две противоположные задачи: прямая, где необходимо найти вероятности нахождения индивида в том или ином состоянии при известных параметрах модели, и обратная, где необходимо найти параметры модели, используя известные характеристики из эксперимента.
Обратные задачи для марковских процессов начали развиваться сравнительно недавно в отличие от методов решения прямых задач. На примере модели страхования в медицине можно видеть, что интенсивности переходов есть не что иное, как количество людей, находящихся в разных «состояниях» системы в определенный момент времени. То есть это заболевающие, выздоравливающие и умершие [1].
Цель работы: определение метода решения обратных задач процесса заболеваемости сахарным диабетом на основе статистической базы в математических модели случайного процесса.
Задачи исследования:
– статистическое исследование базы данных;
– получение математической модели медицинского страхования;
– написание программы на языке программирования С++ для решения обратных задач;
– приближенное решение для математической модели;
– на основе вероятностно-статистического моделирования полученных результатов предсказание и оценка рисков, расчет тарифов при страховании.
Материалы и методы исследования
Вероятностный процесс в той или иной системе с определенным числом состояний и дискретным временем, а также подчиняющийся правилу, что вероятность наступления любого состояния модели в будущем влияет только ее состояние в настоящем, будет называться марковским. В случаем с непрерывным временем в марковском процессе основы были заложены А.Н. Колмогоровым. Он показал, что марковское моделирование дает возможность исследователям видеть изменения системы в каждой из дискретных «точек» времени. Используя статистические данных, можно получить интенсивности переходов между состояниями цепи, они и являются начальными данными самой цепи. Человек, вернее его нахождение в определенном состоянии в определенный момент времени, является основным звеном анализируемой цепи. Самый простой случай это всего два состояния (рис. 1).
Рис. 1. Схема из двух состояний
В данном случае индивид может перейти только из состояния «жив» в состояние «мертв». При разных схемах страхования страховые пособия выплачиваются по-разному. Например, периодические равные платежи идут пока клиент находится в состоянии 1, а после перехода в состояние 2 – прекращаются. Либо производятся при переходе в состояние 2 и т.д. Все эти схемы просты и легко вычисляются.
Рассматривая схему с тремя возможными вариантами: «здоров», «болен», «мертв» – видно, что в этом случае взносы будут выплачиваться при нахождении страхователя в первом состоянии, а выплаты будут осуществляться при нахождении во втором состоянии.
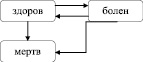
Рис. 2. Схема из трех состояний
Сложность актуарных расчетов в этом случае обуславливается тем, что человек может переходить между состояниями туда и обратно по нескольку раз. Именно поэтому такие переходы при расчетах «блокируются» [2].
Марковская цепь при непрерывном времени выглядит:
Пусть Х(t) состояние человека в возрасте t (t ≥ 0). Зададим случайный процесс {Х(t), t ≥ 0}. Количество состояний будем предполагать счетным {1,2,…,n}. Тогда {Х(t), t ≥ 0} – марковский процесс при любых s, t ≥ 0 и i, j, x(u)∈{1,2,…n},
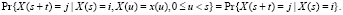
Будущее этого процесса зависит от «прошлого» (в момент времени s) только через «настоящее» (до момента времени s).
Функция вероятности перехода:
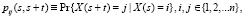
предполагаем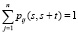 
при любых t ≥ 0 и 
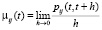, i, j∈{1, 2…n}, i ≠ j.
При i ≠ j μij – это интенсивность перехода из состояния i в состояние j при s, t, u ≥ 0.
Уравнение Колмогорова – Чепмэна имет следующий вид:
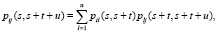i, j∈{1, 2,…n}. (1)
Для получения вероятностей перехода решаем систему дифференциальных уравнений. А полученные вероятности переходов связаны с интенсивностями переходов в прямой и обратной задачах [3].
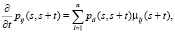(2)
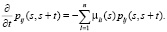(3)
Граничные условия:
,
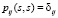где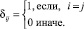 
В случае когда при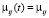 
можно определить функции вероятностей перехода для любого t, мы имеем дело с так называемым однородным марковским процессом относительно времени.
Если в рассматриваемом процессе интенсивности известны, то решение дифференциальных уравнений Колмогорова и будет прямой задачей. А модель с неизвестными интенсивностями (в случае обратной задачи) ведет к оцениванию интенсивностей по имеющимся статистическим исходным данным.
При моделировании схемы марковского процесса необходимо ввести числовую оценку показателя качества, находящуюся внутри определенного интервала. Другими словами – интенсивности переходов между состояниями принадлежат определенному промежутку, у которого границы заданы условиями самого процесса.
Таким образом проверка на попадание величины интенсивности в сам интервал есть решение обратной задачи. Возникает задача регулирования качества, решаемая путем анализа экспериментальных данных. Критерием контроля качества будет являться возможность описания входных данных в рамках модели.
pij(t) известны нам из статистической базы. Зададим характеристику точности измерения:
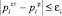, (4)
где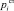 
– табличные данные по вероятности; 
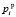– расчетные вероятности (1).
Система имеет решение в пределах некоторого интервала неопределенности mij , характеризуемого некоторым диапазоном вариации Dij (4).
Dij = [min mij , max mij]. (5)
Задачу по поиску интервала, покрывающего область возможных значений, которые можно отнести к характеристикам изучаемого параметра (5) при удовлетворении неравенству (4) ставил еще в 1962 г. основоположник линейного программирования Л.В. Канторович [4].
Результаты исследования и их обсуждение
Исследования проводились при анализе процесса, в котором модель многих состояний, описывала состояния застрахованного лица с заболеванием сахарного диабета. Статистические данные по заболеванию сахарным диабетом получены в Медицинском информационно-аналитическом центре при министерстве здравоохранения Республики Башкортостан.
Рассматриваемая модель состоит из четырех состояний: «здоров», «болен сахарным диабетом, инсулинонезависимый тип», «болен сахарным диабетом, инсулинозависимый тип», «мертв», где λij – интенсивности переходов между состояниями.
Рис. 3. Схема состояний
По представленной на рис. 3 схеме составим систему дифференциальных уравнений Колмогорова для поиска вероятности нахождения индивида в каждом из состояний:
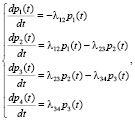(6)
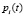
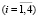– вероятность состояния Ai.
Изначально предполагаем, что индивид находится в состоянии «здоров», т.е. задаем следующие начальные условия:
, 
, 
,
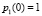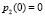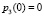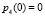. (7)
В любой момент времени выполняется нормировочное условие, т.е. индивид находится в каком-то из четырех состояний:
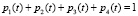. (8)
Решаем прямую и обратную задачи. Соответственно ищем решение уравнений Колмогорова при известных интенсивностях переходов, а при неизвестных интенсивностях переходов – по статистическим данным оцениваем интенсивности переходов.
Имея средние значения интенсивностей, которые были найдены на базе статистических данных, решена обратная задача методом Рунге – Кутты 4 порядка, реализованного в программе, написанной на языке программирования С++. Вычисления были реализованы на суперкомпьютере математического факультета БашГУ.
Для вероятности p1 из описанной схемы выражаем интенсивность перехода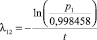 
. Другие интенсивности выражаем таким же образом. Анализируя средние значения показателей интенсивностей, выводим расчетные значения вероятностей нахождения в состояниях A1 – «здоров», A2 – «болен сахарным диабетом инсулинонезависимый тип», A3 – «болен сахарным диабетом инсулинозависимый тип», A4 – «мертв».
На основании сопоставимости расчетных и экспериментальных данных можно заключить, что рассматриваемая модель применима на практике для задач определения, проверки, прогноза необходимого диапазона средств на борьбу с болезнью [5].
Определяем из системы (4) области неопределенности по интенсивностям λij, взяв расчетные и экспериментальные вероятности. Для получения интервала необходимых денежных средств используем интервал изменения интенсивностей [6].
В данный момент лечение сахарного диабета в большинстве случаев сводится к компенсации болезни, кроме того сахарный диабет второго типа неизлечим, лечение в этом случае не может устранить саму причину заболевания, и оно сводится лишь к исключению симптомов и осложнений, которых на сегодняшний день существует огромное множество. Сама болезнь до конца не изучена, от нее самой как таковой не умирают, а умирают от вызванных ею осложнений. Эта болезнь уже сейчас считается мировой проблемой, которая из года в год многократно растет. Выделяемые средства на борьбу с сахарным диабетом могут варьироваться в достаточно большом интервале от 22 000 руб. до 156 000 руб. в зависимости от осложнений. Например, в 2013 г. зарегистрировано больных сахарным диабетом в России по данным ГосРегистра примерно 3 800 000 человек. По данным International Diabetes Federation (IDF) на лечение одного больного тратится в среднем 22750 рублей в год.
Величина расходов лежит в интервале [8,3 *109; 5,89*1011], полученном на основе математического ожидания. Интервал изменения средств [5,3*1010; 8,2*1010] найден из интервала изменения интенсивности перехода. Видим, что интервал изменения средств включает полученный нами интервал. То есть рассмотренная методология поиска интервала изменения необходимых денежных средств применима для реальных задач, возникающих в страховании и не обязательно медицинском.
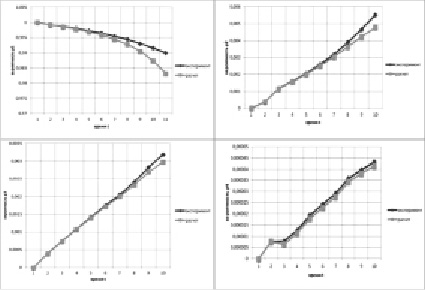
Рис. 4. Графики сравнения расчета и эксперимента
Заключение
Проведенные исследования на основе вероятностно-статистического моделирования, опирающиеся на реальные данные, полученные в Медицинском информационно-аналитическом центре при министерстве здравоохранения Республики Башкортостан, показали, что разработанная схема-модель, а также компьютерная программа могут быть использованы для предсказания и управления, а полученные результаты могут служить основой для дальнейших исследований в случаях отличных от рассматриваемого процесса заболевания сахарным диабетом. Проделанный анализ дает страховщикам в области медицины реальный механизм расчета страховых ставок.