Известно, что при современных тенденциях повышения удельных мощностей двигателей внутреннего сгорания, а также к более высоким скоростям и меньшим размерам для микроэлектронных устройств постоянно возрастает количество теплоты, которое необходимо отводить от нагретых узлов и деталей. Применение различных теплопроводящих жидкостей для отвода тепла является одним из наиболее распространенных и эффективных способов. Эффективность современных конструкций охлаждающих устройств, как и обычный способ увеличения интенсивности теплопередачи, практически достигли своего предела. Известно, что обычные охлаждающие жидкости (вода, масла, гликоли, фторуглероды), обладают достаточно низкой теплопроводностью (табл. 1), что является ограничивающим фактором в современных конструкциях систем охлаждения. Для увеличения их теплопроводности можно создать многофазную (минимум двухфазную) дисперсную среду, где роль дисперсии выполняют частицы со значительно большим коэффициентом теплопроводности, чем базовая жидкость. Максвелл в 1881 году предложил добавить твердые частицы с высокой теплопроводностью в базовую теплопроводящую охлаждающую жидкость.
Идея состоит в том, чтобы смешать металлические материалы, такие как серебро, медь, железо, и неметаллические материалы, такие как глинозем, CuO, SiC и углеродные трубки, обладающие более высокой теплопроводностью по сравнению с базовой теплопроводящей жидкостью с меньшим коэффициентом теплопроводности. Первоначально твердые частицы (такие как серебро, медь, железо, углеродные трубки, обладающие более высокой теплопроводностью по сравнению с базовой жидкостью) микронных и даже миллиметровых размеров были смешаны с базовыми жидкостями с получением суспензий. Достаточно большой размер применяемых частиц и трудности в производстве наноразмерных частиц стали ограничивающими факторами в применении таких суспензий. Указанная проблема была решена работами сотрудников Аризонской национальной лаборатории S. Choi и J. Eastman, которые провели эксперименты с металлическими частицами нанометровых размеров [3]. Они соединяли различные металлические наночастицы и наночастицы металлических окислов с различными жидкостями и получили очень интересные результаты. Эти суспензии наноструктурированных материалов были названы «наножидкостями».
Таблица 1
Сравнение коэффициентов теплопроводности материалов для наножидкостей
|
Материалы |
Коэффициент теплопроводности, Вт/(м·К) |
|
|
Углерод |
Графен |
~5000 |
|
Алмаз |
2300 |
|
|
УНТ |
~2000 |
|
|
Графит |
110‒190 |
|
|
Металлические материалы |
Серебро |
429 |
|
Медь |
401 |
|
|
Алюминий |
237 |
|
|
Теплопроводящие жидкости |
Вода |
0.613 |
|
Этиленгликоль |
0.253 |
|
|
Моторное масло |
0.145 |
|
С целью разработки современных инновационных охлаждающих жидкостей для систем охлаждения высокофорсированных теплоэнергетических устройств нами были рассмотрены двухфазные системы, состоящие из базовой среды (вода, этиленгликоль, масла и др.) и наночастиц, т.е. частиц с характерными размерами от 1 до 100 нм. Важной особенностью наножидкостей является то, что даже при добавлении небольшого количества наночастиц они показывают серьезное повышение в теплопроводности (иногда более, чем в 10 раз). Причем повышение теплопроводности наножидкости зависит от температуры – с ростом температуры увеличивается повышение коэффициента теплопроводности.
При создании таких наножидкостей, представляющих собой двухфазную систему, необходим надежный и достаточно точный метод измерения коэффициента теплопроводности.
Нами рассмотрены разные методы измерения коэффициента теплопроводности для жидкостей [1, 2, 4]. В результате проведенного анализа был выбран «3ω-проводной» метод для измерения теплопроводности наножидкостей с достаточно высокой точностью [5].
«3ω-проводной» метод используется для одновременного измерения теплопроводности и температуропроводности материалов. Он основан на измерении повышения температуры, зависящей от времени в источнике тепла, то есть горячем проводе, который погружен в жидкость для тестирования. Металлическая проволока одновременно служит электрическим нагревателем сопротивления и термометром сопротивления. Металлические проволоки изготавливаются крайне малыми в диаметре (несколько десятков мкм). Повышение температуры проволоки достигает обычно 10 °C и влиянием конвекции при этом можно пренебречь.
Металлическая проволока длиной L и радиусом r, взвешенная в жидкости, действует как нагреватель и термометр сопротивления, как показано на рис. 1.
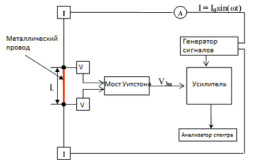
Рис. 1. Схема установки метода «3ω горячей проволоки» для измерения теплопроводности жидкости
Сущность используемого метода определения коэффициента теплопроводности заключается в следующем. Переменный ток течет через металлический провод (нагреватель). Характеристика переменного тока определяется уравнением
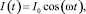 (1)
(1)
где I0 – является амплитудой переменного синусоидального тока; ω – частота тока; t – время.
Переменный ток протекает через проволоку, действуя как нагреватель. В соответствии с законом Джоуля ‒ Ленца определяется количество теплоты, выделяющееся при прохождении по проводнику электрического тока:
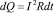 (2)
(2)
и представляет собой суперпозицию источника постоянного тока и 2ω модулированного источника тепла,
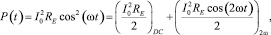 (3)
(3)
где RE является электрическим сопротивлением металлической проволоки в условиях эксперимента, и оно является функцией температуры.
Выделившаяся тепловая мощность порождает изменение температуры в нагревателе, которое также является суперпозицией компоненты постоянного тока и компоненты 2ω переменного тока:
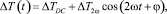 (4)
(4)
где ΔTDC – амплитуда изменения температуры под действием постоянного тока; ΔT2ω – амплитуда изменения температуры под действием переменного тока; φ – сдвиг фазы, индуцированный нагревом массы образца.
Электрическое сопротивление провода зависит от температуры и это и есть 2ω компонент переменного тока в сопротивлении проволоки:
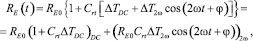 (5)
(5)
где Crt – температурный коэффициент сопротивления для металлического провода; RE0 – справочное сопротивление нагревателя при температуре T0.
Обычно T0 это температура объемного образца.
Напряжение на металлическом проводе может быть получено как,
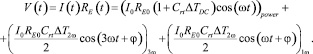 (6)
(6)
В уравнении (6) напряжение на проводе содержит: падение напряжения из-за сопротивления постоянного тока провода при 1ω и два новых компонента, пропорциональные повышению температуры в проводе при 3ω и при 1ω. 3ω компонента напряжения 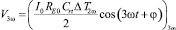 может быть извлечена при помощи усилителя, а затем используется для вывода амплитуды изменения температуры при 2ω:
может быть извлечена при помощи усилителя, а затем используется для вывода амплитуды изменения температуры при 2ω:
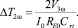 (7)
(7)
Частотная зависимость изменения температуры ΔT2ω получена изменением частоты переменного тока при постоянном напряжении V1ω. В то же самое время зависимость изменения температуры ΔT2ω от частоты может быть аппроксимирована как
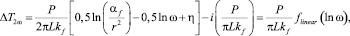 (8)
(8)
где αf – коэффициент температуропроводности; kf – коэффициент теплопроводности базовой жидкости; η – константа.
Изменение температуры при частоте 2ω в металлической проволоке может быть выведено при помощи компоненты напряжения частоты 3ω, как показано в уравнении (8). Коэффициент теплопроводности жидкости kf определяется по наклону 2ω изменения температуры металлической проволоки по отношению к частоте ω,
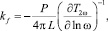 (9)
(9)
где Р – применяемая мощность; ω – является частотой приложенного электрического тока; L – длина металлической проволоки; ΔT2ω – амплитуда изменения температуры на частоте 2ω в металлической проволоке.
3ω-проводной метод имеет несколько преимуществ перед традиционным методом горячего провода:
1) температурные колебания могут быть достаточно маленькими (ниже 1K, по сравнению с приблизительно 5K для метода горячей проволоки) в исследуемой жидкости, чтобы сохранить постоянные свойства жидкости;
2) фоновые шумы, такие как изменение температуры, имеют гораздо меньшее влияние на результаты измерений.
Эти преимущества делают этот метод идеально подходящим для измерения температурной зависимости коэффициента теплопроводности наножидкостей.
Установка для измерения коэффициента теплопроводности включает следующие компоненты: мост Уинстона; генератор сигналов; анализатор спектра; осциллограф.
Мост Уинстона представляет собой схему, применяемую для сравнения неизвестного сопротивления Rx с известным сопротивлением R0. Схема моста приведена на рис. 2. Четыре плеча моста Уинстона АВ, ВС, АД и ДС представляют собой сопротивления Rх, R0, R1 и R2 соответственно. В диагональ ВД включается гальванометр, а в диагональ АС подсоединяется источник питания.
Если соответствующим образом подобрать величины переменных сопротивлений R1 и R2, то можно добиться равенства потенциалов точек В и Д: φВ = φД. В этом случае ток через гальванометр не пойдет, то есть Ig = 0. При этих условиях мост будет сбалансирован, и можно найти неизвестное сопротивления Rх. Для этого воспользуемся правилами Кирхгофа для разветвленных цепей. Применяя первое и второе правила Кирхгофа, получим
Rх = R0·R1/R2.
Точность в определении Rх указанным методом в большой степени зависит от выбора сопротивлений R1 и R2. Наибольшая точность достигается при R1 ≈ R2.
Генератор сигналов выступает в качестве источника электрических колебаний в диапазоне 0,01 Гц – 2 МГц с высокой точностью (с дискретностью через 0,01 Гц). Марка генератора сигналов Г3-110.
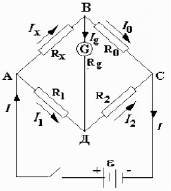
Рис. 2. Схема моста Уинстона
Анализатор спектра предназначен для выделения 3ω составляющей спектра. Перед началом работы анализатор спектра тестировался на соответствие величины напряжения третьей гармоники. Для этого на вход анализатора спектра подается сигнал с генератора Г3-110 и параллельно – на широкополосный цифровой вольтметр. Эффективное значение амплитуды напряжения сравнивалось на анализаторе спектра и вольтметре. Расхождение значений составило 2 %. Калибровка анализатора спектра также выполнялась на внутреннем тесте прибора, на частоте 10 кГц. Величина сигнала на несущей частоте составила 80 мВ.
Осциллограф C1-114/1 предназначен для исследования формы электрических сигналов.
Перед началом исследования нагреватель (проволока) должен быть помещен в исследуемый образец жидкости. Проволока не должна касаться стенок сосуда. Далее производили сканирование по частоте в диапазоне от 100 до 1600 Гц. На анализаторе спектра при исследуемой частоте фиксируется величина сигнала 1, 2, 3 гармоники в автоматическом режиме.
Для измерения амплитуды силы тока использовали последовательно включенный в цепь резистор сопротивлением ~ 0,47 Ом. Величина должна быть такая, чтобы она не превышала номинал измерительного плеча порядка 1 Ом. С помощью осциллографа находили напряжение U. Зная R и U, находили амплитуду силы тока I0. Для расчета приложенной мощности измеряется напряжение в цепи.
Вначале исследуется широкий частотный диапазон. Определяется более узкая область частот, где линейность графика наиболее высока. Затем в выбранной области частот производится измерение с более мелким шагом частоты.
В табл. 2 представлены результаты измерения коэффициента теплопроводности наножидкости, представляющей собой 0,35 % суспензию оксида графена в базовой жидкости (воде), с помощью медной изолированной проволоки длиной 19 см, диаметром 100 мкм, при температуре 26 °С для частотного диапазона 780...840 Гц.
На рис. 3 приведен общий вид стенда для измерения коэффициента теплопроводности жидкости.
В табл. 3 представлена зависимость коэффициента теплопроводности суспензии оксида графена от его концентрации в жидкости при температуре 26 °С. Измерения коэффициентов теплопроводности наножидкости осуществлялись при различной концентрации оксида графена от 0 до 1,25 %.
Таблица 2
Результаты измерения коэффициента теплопроводности наножидкости
|
Частотный диапазон |
Круговая частота |
Сила тока |
Амплитуда напряжения третьей гармоники |
Изменение температуры |
Логарифм круговой частоты |
Мощность |
Наклон графика |
Коэффициент теплопроводности |
|
ν, Гц |
ω, с–1 |
I0, A |
U3ω, В |
ΔT2ω, K |
ln(ω), с–1 |
P, Вт |
T/ln(ω) |
k, Вт/м·K |
|
780 |
4900,88 |
0,46 |
0,000044 |
0,138 |
8,50 |
0,28 |
‒0,153 |
0,75 |
|
790 |
4963,72 |
0,46 |
0,000042 |
0,133 |
8,51 |
0,27 |
‒0,153 |
0,74 |
|
800 |
5026,55 |
0,46 |
0,000041 |
0,131 |
8,52 |
0,26 |
‒0,153 |
0,72 |
|
810 |
5089,38 |
0,45 |
0,000041 |
0,130 |
8,53 |
0,26 |
‒0,153 |
0,71 |
|
820 |
5152,21 |
0,45 |
0,000040 |
0,128 |
8,55 |
0,25 |
‒0,153 |
0,69 |
|
830 |
5215,04 |
0,45 |
0,000038 |
0,124 |
8,56 |
0,25 |
‒0,153 |
0,68 |
|
840 |
5277,88 |
0,44 |
0,000038 |
0,123 |
8,57 |
0,25 |
‒0,153 |
0,67 |

Рис. 3. Общий вид стенда для измерения коэффициента теплопроводности жидкости
В табл. 3 также приведены значения коэффициентов теплопроводности, определенные по формуле Максвелла.
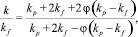 (10)
(10)
где k – коэффициент теплопроводности наножидкости; kf – коэффициент теплопроводности базовой жидкости; kp – коэффициент теплопроводности дисперсной фазы (наночастиц); φ – величина объемной фазы каждой из фаз дисперсий.
Таблица 3
Коэффициент теплопроводности суспензии оксида графена
|
Концентрация оксида графена |
Измеренный коэффициент теплопроводности наножидкости |
Коэффициент теплопроводности наножидкости по Максвеллу |
Отношение коэффициентов теплопроводности |
|
|
С, % |
kэкспер, Вт/м·К |
kтеор, Вт/м·К |
kэксп/kтеор |
kэксп/kтабл. воды |
|
0,00 |
0,59 |
0,590 |
1,00000 |
1,00000 |
|
0,35 |
0,69 |
0,609 |
1,13300 |
1,16949 |
|
1,00 |
0,75 |
0,618 |
1,21359 |
1,27119 |
|
1,25 |
1,00 |
0,623 |
1,60514 |
1,69492 |
Отношение коэффициентов теплопроводности kэксп/kтеор и kэксп/kтабл. воды приведены на рис. 4.
Такие отклонения экспериментальных данных от предсказанных классическим Максвелловским уравнением, по нашему мнению, могут быть связаны с физическими механизмами увеличения теплопроводности наножидкости, а именно:
– за счет броуновского движения частиц; перемешивание жидкости создает микро-конвективный эффект, тем самым повышая энергию теплопереноса;
– переносом тепла по механизму перколяции преимущественно вдоль кластерных каналов, образующихся в результате агломерации наночастиц, пронизывающих всю структуру растворителя (обычной жидкости);
– молекулы базовой жидкости образуют высоко ориентированные слои вокруг наночастиц, таким образом увеличивая объемную долю наночастиц.
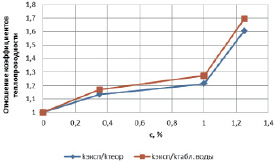
Рис. 4. Зависимость отношения коэффициентов теплопроводности от концентрации оксида графена
Работа выполнена с привлечением оборудования Центра коллективного пользования научным оборудованием «Диагностика микро- и наноструктур» при финансовой поддержке Министерства образования и науки РФ.
Рецензенты:
Епархин О.М., д.т.н., профессор, директор Ярославского филиала ФГБОУ ВПО «Московский государственный университет путей сообщения», г. Ярославль;
Амиров И.И., д.ф.-м.н., научный сотрудник Ярославского филиала ФГБУН «Физико-технологический институт» Российской академии наук, г. Ярославль.
Работа поступила в редакцию 28.07.2014.
Библиографическая ссылка
Жаров А.В., Савинский Н.Г., Павлов А.А., Евдокимов А.Н. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ИЗМЕРЕНИЯ ТЕПЛОПРОВОДНОСТИ НАНОЖИДКОСТИ // Фундаментальные исследования. 2014. № 8-6. С. 1345-1350;URL: https://fundamental-research.ru/ru/article/view?id=34766 (дата обращения: 07.03.2026).



