Несмотря на наличие существенных преимуществ по сравнению с широко распространенными зубчатыми колесами, нарезанными на приближенных к гиперболоиду заготовках, точные гиперболоидные зубчатые колеса [3] (по классификации Грибанова В.М.) не нашли пока широкого распространения в машиностроении. Это обусловлено, в первую очередь, технологической сложностью изготовления гиперболоидных колес. В течение достаточно продолжительного времени [1] проводятся исследования в области формообразования зубьев гиперболоидных зубчатых колес. Предлагались различные подходы [2, 4, 6], ориентированные как на воспроизведение кинематики зацепления на основе применения конструктивно сложных технологических систем с применением универсального оборудования, так и применения оборудования с числовым программным управлением.
Геометрические особенности гиперболоидных зубчатых колес не позволяют применять традиционные для зубонарезания технологии и инструмент. Воспроизведение зацепления реализуемо только на отделочных операциях, например при шевинговании и хонинговании.
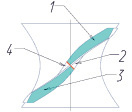
Кривизна различного знака по длине боковой поверхности зуба затрудняет доступ режущего инструмента (рис. 1), существенно усложняет обработку традиционными методами зубонарезания. Линия перегиба расположена с некоторым смещением относительно горлового сечения. При достижении режущим инструментом при традиционных методах зубонарезания линии перегиба возникает необходимость в пространственном изменении относительного положения инструмента и заготовки, что вызовет подрезку материала заготовки. Поэтому исследование кинематики формообразования зубьев гиперболоидной передачи является актуальной задачей.
Формообразование боковых поверхностей зубьев гиперболоидных зубчатых колес с учетом их геометрических особенностей на основе кинематики движения производящей линии – режущей кромки инструмента – наиболее эффективно реализуется при многоосевой (не менее 5 координат) обработке на станках с ЧПУ. Однако инструментальные средства CAM пакетов, хотя и позволят запрограммировать обработку, но маловероятно, что обеспечат достаточную производительность при требуемой точности. Производительность обработки можно существенно повысить. К особенностям геометрии следует отнести наличие зон выпуклых и вогнутых поверхностей на боковых сторонах зубьев, а соответственно, участков где изменяется характер поверхности (рис. 1, б). С учетом условий благоприятного осуществления процесса резания, каждый из участков целесообразно обрабатывать отдельно.
Обработку боковых поверхностей зубчатого колеса на станке с ЧПУ целесообразно осуществлять дисковыми и концевыми фрезами.
Траектория движения режущих кромок инструмента на чистовом этапе обработки для достижения высокой точности, достижимой на данном станке с применением заданного инструмента, может быть рассчитана через уравнение боковой поверхности зуба. Боковая поверхность зуба формируется пространственной трансляцией отрезка прямой (рис. 2), следовательно, является линейчатой поверхностью, хотя в сечениях, перпендикулярных оси вращения колеса, боковые поверхности представляются кривыми.
Расчет уравнения боковой поверхности можно осуществлять несколькими способами. Во-первых, используя методику, предложенную в работе [5].
Рассмотрим уравнения боковых поверхностей зубьев гиперболоидных колес, полученные с учетом сдвига режущего инструмента при i ≠ 1 и δ ≠ 1.
 а)
а)
 б)
б)
Рис. 1. Участки поверхности зуба гиперболоидного зубчатого колеса: а) трехмерная модель, б) эскиз зуба колеса: 1, 3 – рабочие участки; 2, 4 – «интерферируемые» участки [2]
Координаты произвольной точки M2, принадлежащей прямой LM, жестко связанной со вторым колесом, в неподвижной системе координат 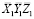 будут:
будут:
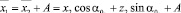 ;
;
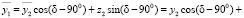
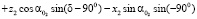 ; (1)
; (1)
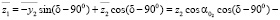
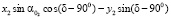 ,
,
где δ – угол между осями вращения колес.
Тогда уравнение кривой, которую описывает точка M2 в подвижной системе координат первого колеса, запишется:
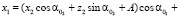
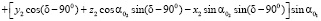
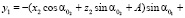
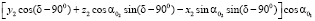 (2)
(2)
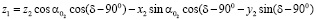 ,
,
где α01 = ± α02∙i12. Знак плюс берется, если направления ω1 и ω2 совпадают, в противоположном случае – знак минус.
Данный подход позволяет определить уравнения боковых поверхностей, участвующих в зацеплении для обеих колес, осуществив аналогичные манипуляции. Расчет осуществляется раздельно для каждого колеса по участкам зуба.
При пятикоординатной обработке важными параметрами, на основе которых формируется управляющая программа для станка с ЧПУ, является множество точек, образующих траекторию движения точки трассировки фрезы, а также ориентация режущего инструмента относительно геометрии заготовки. Так как боковая поверхность формируется перемещением образующей LM при закоординированном вращении гиперболоидов, то боковая поверхность зуба является линейчатой поверхностью. Движение инструмента необходимо осуществлять таким образом, чтобы он работал на растяжение. Ориентация инструмента определяется в естественных координатах, связанных с траекторией движения инструмента, хотя для CAM системы, в которой предполагается осуществлять разработку управляющей программы, удобнее будет определить ориентацию инструмента с помощью вспомогательных кривых, представляющих собой годографы вектора ориентации инструмента по участкам зуба.
В точке перегиба нормаль меняет направление, соответственно закон ориентации инструмента при переходе через точку перегиба необходимо изменять.
Для расчета можно использовать также кинематический метод расчета [7], позволяющий еще на этапе формирования исходных данных, задаться геометрическими зависимостями параметров инструмента и производящей линии (рис. 3, рис. 4). При расчете необходимо задаться ограничениями. Во-первых, расстояние по нормали от нижней кромки обрабатываемой поверхности до оси вращения фрезы – величина постоянная. Это означает, что по нижнему ребру поверхности коническая режущая часть осуществляет обработку одним и тем же диаметром. Во-вторых, ось вращения фрезы лежит в плоскости, образованной образующей AB, и нормалью к нижнему ребру в точке B. В-третьих, образующая AB совпадает с образующей конической части инструмента, данный конус описывают режущие кромки фрезы при ее вращении.
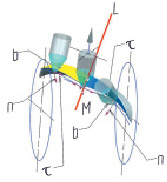
Рис. 2. К расчету траектории движения инструмента и ориентации инструмента: LM – производящая линия, τ – орт-вектор касательной, n – орт-вектор нормали, b – орт-вектор бинормали
Чистовую обработку предполагается осуществлять боковыми режущими кромками концевой фрезы. Для более благоприятной нагрузки инструмента, предварительно обрабатывается область в районе горлового сечения, а затем по отдельности, от горлового сечения – в направлении торцов заготовки.
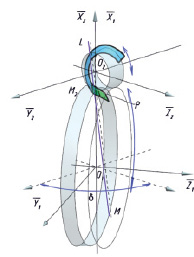
Рис. 3. К определению траектории формообразующего движения режущей кромки
Рассчитанную по методике [7] поверхность, описываемую пространственным перемещением линии LM, необходимо пересчитывать для двух точек режущей кромки фрезы A и B в системе координат, связанной с заготовкой. Точка B должна удовлетворять условию нахождения ее на уровне, соответствующем ножке зуба. Точку А можно рассчитывать произвольно, учитывая ограничение нахождения ее на режущей кромке. Режущая кромка должна превышать расстояние от ножки до вершины зуба. Точка, принадлежащая оси фрезы, располагается в направлении нормали к траектории, описываемой точкой B для вогнутых участков и в противоположном направлении – для выпуклых, на расстоянии радиуса фрезы в данном ее сечении. Плоскость, в которой располагается ось фрезы, определяется вышеупомянутой точкой и отрезком АВ. Ось фрезы проходит под углом наклона боковой поверхности к отрезку АВ. Через геометрические соотношения, характеризующие инструмент, рассчитываются координаты точки Р – являющиеся координатами соответствующей траектории движения инструмента. Ориентация оси инструмента рассчитывается через координаты точки Р и любой другой точки, лежащей на оси. Рассчитанные таким образом траектория и годограф ориентации инструмента позволяют в современных CAM системах разработать управляющую программу для пятикоординатной обработки боковой поверхности зуба, моделируя движения производящей линии. При расчете необходимо учитывать ограничения, накладываемые боковой поверхностью соседнего зуба.
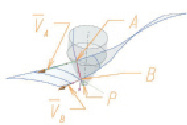
Рис. 4. К определению траектории движения инструмента по методу кинематического формообразования: AB – образующая, P – точка трассировки
Таким образом, формообразование боковой поверхности зубчатых колес на основе однополостного гиперболоида вращения возможно осуществить концевой фрезой с использованием многокоординатных станков с ЧПУ. Для исключения подрезания боковой поверхности зуба в месте перехода кривизны одного знака на другой и более благоприятной нагрузки инструмента, зубофрезерование целесообразно вести, сначала обработав область горлового сечения, а затем в направлении торцов заготовки с обработкой каждого из участков боковой поверхности зуба отдельно. При формировании управляющей программы необходимо вводить алгоритм управления ориентацией инструмента при обработке боковой поверхности зубьев.
Рецензенты:
Сахапов Р.Л., д.т.н., профессор, заведующий кафедрой «Дорожно-строительные машины», ФГБОУ ВПО «Казанский государственный архитектурно-строительный университет Минобрнауки РФ», г. Казань;
Шамсутдинов Ф.-Р.А., д.т.н., профессор, заведующий кафедрой «Общеинженерные дисциплины», ФГОУ ВПО «Казанский государственный аграрный университет Минсельхоза РФ», г. Казань.
Работа поступила в редакцию 30.12.2014.
Библиографическая ссылка
Печенкин М.В., Абзалов А.Р. КИНЕМАТИКА ФОРМООБРАЗОВАНИЯ БОКОВОЙ ПОВЕРХНОСТИ ЗУБЬЕВ ГИПЕРБОЛОИДНОЙ ПЕРЕДАЧИ КОНЦЕВЫМ ИНСТРУМЕНТОМ // Фундаментальные исследования. – 2014. – № 12-11. – С. 2310-2314;URL: https://fundamental-research.ru/ru/article/view?id=36686 (дата обращения: 26.04.2024).



